8.3 Polygons

8.3 Polygons (EMCJ9)

temp text

Proportionality in polygons: A plane, closed shape consisting of three or more line segments.

In previous grades we studied the properties of the following polygons:

Triangle		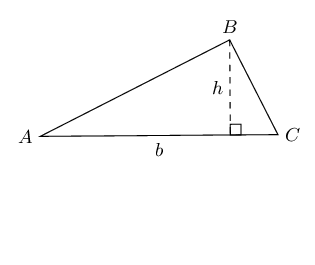Area $= \frac{1}{2}b \times h$
Parallelogram		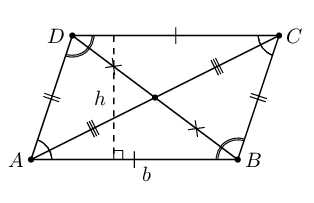Area $= b \times h$
Rectangle		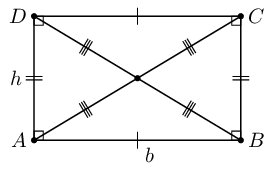Area $= b \times h$
Rhombus		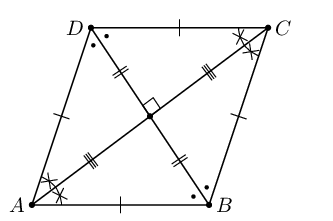Area $= \frac{1}{2} AC \times BD$

Square		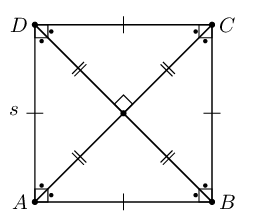Area $= s^{2}$
Trapezium		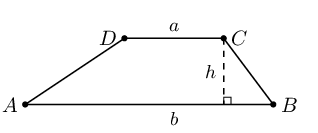Area $= \frac{1}{2}(a + b) \times h$
Kite		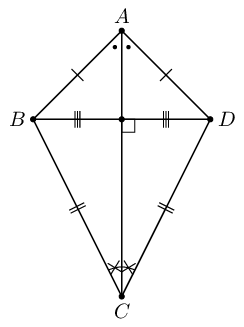Area $= \frac{1}{2}(AC \times DB)$

Worked example 1: Properties of polygons

$ABCD$ is a rhombus with $BD = \text{12}\text{ cm}$ and $AB:BD = 3:4$.

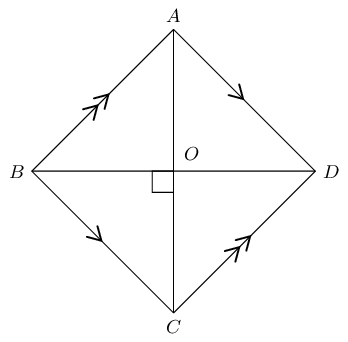
Calculate the following (correct to two decimal places) and provide reasons:

Length of $AB$.
Length of $AO$.
Area of $ABCD$.

Use the ratio to determine the length of $AB$

\begin{align*} AB:BD &= 3:4 \\ \therefore \frac{AB}{BD} &= \frac{3}{4} \\ \frac{AB}{12} &= \frac{3}{4} \\ AB &= 12 \times \frac{3}{4} \\ &= \text{9}\text{ cm} \end{align*}

Calculate the length of $AO$

We use the properties of a rhombus and the theorem of Pythagoras to find $AO$.

\[\begin{array}{rll} BD &= \text{12}\text{ cm} & \\ BO &= \text{6}\text{ cm} & \text{(diagonals bisect each other)} \\ \text{In } \triangle ABO, \quad A\hat{O}B &= \text{90}° & (\text{diagonals intersect at } \perp )\\ AO^{2} &= AB^{2} - BO^{2} & (\text{Pythagoras}) \\ &= 9^{2} - 6^{2} & \\ \therefore AO &= \sqrt{ 45} & \\ &= \text{6,71}\text{ cm} \end{array}\]

Determine the area of rhombus $ABCD$

\begin{align*} \text{Area } ABCD &= \frac{1}{2} AC \times BD \\ &= \frac{1}{2} (2 \times \sqrt{45})(12) \\ &= \text{80,50}\text{ cm$^{2}$} \end{align*}

Proportionality of polygons

Textbook Exercise 8.3

Calculate $MN$ (correct to $\text{2}$ decimal places).

\[\begin{array}{rll} QN &= 10 & \\ \therefore NP &= 2 \times QN & (\text{diagonals bisect each other}) \\ &= 20 & \\ \text{In } \triangle NOP, \quad \hat{O} &= \text{90}° &(MNOP \text{ rectangle }) \\ \text{Let } MN &= 5x & \\ \text{And } NO &= 3x & \\ NP^{2} &= NO^{2} + OP^{2} & (\text{Pythagoras}) \\ (20)^{2} &= (3x)^{2} + (5x)^{2} & \\ 400 &= 9x^{2} + 25x^{2} & \\ 400 &= 34x^{2} & \\ \therefore x &= \sqrt{\frac{400}{34}} & \\ &= \text{3,43} \ldots & \\ \therefore MN &= 5x = \text{17,15}\text{ cm} & \end{array}\]

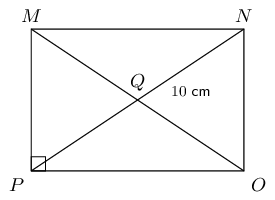
Calculate the area of $\triangle OPQ$ (correct to $\text{2}$ decimal places).

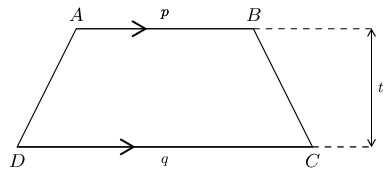
Consider the trapezium $ABCD$ shown below. If $t:p:q = 2:3:5$ and area $ABCD = \text{288}\text{ cm$^{2}$}$, calculate $t, p \text{ and } q$.

\begin{align*} \text{Let } t &= 2x \\ \text{And } p &= 3x \\ \text{And } q &= 5x \\ \text{Area } ABCD &= \frac{1}{2} (p + q) \times t \\ 288 &= \frac{1}{2} (3x + 5x ) \times 2x \\ 288 &= 8x^{2} \\ 36 &= x^{2} \\ \therefore 6 &= x \quad (\text{length always positive}) \\ \therefore t &= 2(6) = \text{12}\text{ cm} \\ p &= 3(6) = \text{18}\text{ cm} \\ q &= 5(6) = \text{30}\text{ cm} \end{align*}

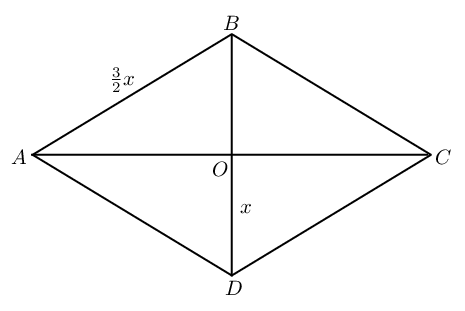
$ABCD$ is a rhombus with sides of length $\frac{3}{2}x$ millimetres. The diagonals intersect at $O$ and length $DO = x$ millimetres. Express the area of $ABCD$ in terms of $x$.

\begin{align*} AD &= \frac{3}{2}x \\ DO&=x \\ AO^2&=\left ( \frac{3}{2}x \right )^2-x^2 \quad (\text{ Pythagoras})\\ &=\frac{9}{4}x^2-x^2\\ &=\frac{5}{4}x^2 \\ \therefore AO&=\frac{x\sqrt{5}}{2} \\ \therefore AC&=x\sqrt{5} \\ \text{Area }&=\frac{1}{2}AC\times BD\\ &=\frac{1}{2}\times x \sqrt{5} \times 2x \\ &= \sqrt{5} x^2 \end{align*}

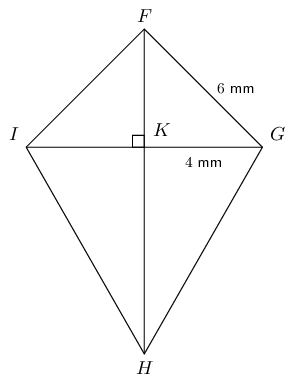
Determine $FH$ (correct to the nearest integer).

\begin{align*} \frac{GH}{FI} &= \frac{5}{2} \\ \text{And } FG &= FI \quad (\text{adj. sides of kite equal}) \\ \frac{GH}{FG} &= \frac{5}{2} \\ \frac{GH}{6} &= \frac{5}{2} \\ \therefore GH &= \text{15}\text{ mm} \\ \text{In } \triangle FGK, \quad FG^{2} &= GK^{2} + FK^{2} \\ FK^{2} &= 6^{2} - 4^{2} \\ &= 36 - 16 \\ \therefore FK &= \sqrt{20} \\ \text{In } \triangle GKH, \quad GH^{2} &= GK^{2} + FH^{2} \\ 15^{2} &= 4^{2} + KH^{2} \\ 225 - 16 &= KH^{2} \\ \therefore KH &= \sqrt{209} \\ FH &= FK + KH \\ &= \sqrt{20} + \sqrt{209} \\ &= \text{19}\text{ mm} \end{align*}

Calculate area $FGHI$.

\begin{align*} \text{Area } FGHI &= \frac{1}{2} GI \times FH \\ &= \frac{1}{2} (4 + 4)(19) \\ &= \text{76}\text{ mm$^{2}$} \end{align*}

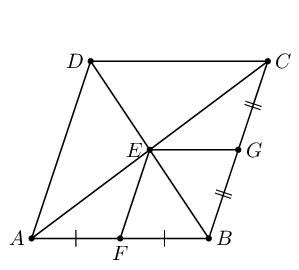
$ABCD$ is a rhombus. $F$ is the mid-point of $AB$ and $G$ is the mid-point of $CB$. Prove that $EFBG$ is also a rhombus.

\[\begin{array}{rll} AF &= FB & (\text{given}) \\ AE &= EC & (\text{diagonals bisect}) \\ \therefore FE &\parallel BC & \\ \therefore FE &\parallel BG & \\ \therefore FE &= \frac{1}{2} BG & (\text{mid-point th.}) \\ FE &= BG & \\ \therefore EFBG & \text{ is a parallelogram} & (\text{one pair opp. sides} = \text{ and } \parallel) \\ \therefore FB &\parallel EG & (\text{opp. sides of parm.}) \\ \text{And } AB &= BC & (\text{adj. sides of rhombus}) \\ \therefore \frac{1}{2} AB &= \frac{1}{2} BC & \\ \therefore FB &= BG = GE = EF & \\ \therefore EFBG &(\text{is a rhombus}) & (\text{parm. with }4 \text{ equal sides}) \end{array}\]

8.2 Ratio and proportion

Table of Contents

8.4 Triangles