8.2 Ratio and proportion

8.2 Ratio and proportion (EMCJ8)

Ratio

A ratio describes the relationship between two quantities which have the same units. We can use ratios to compare weights, heights, lengths, currencies, etc. A ratio is a comparison between two quantities of the same kind and has no units.

Example: if the length of a rectangle is \(\text{20}\) \(\text{cm}\) and the width is \(\text{60}\) \(\text{cm}\), then we can express the ratio between the length and width of the rectangle as:

• The ratio of \(\frac{1}{3}\) describes the length of the rectangle relative to its width.
• A ratio written as a fraction is usually given in its simplest form.

• A ratio gives no indication of actual length. For example,

  \[\frac{\text{length}}{\text{width}} = \frac{\text{50}\text{ cm}}{\text{150}\text{ cm}} \enspace \text{also gives a ratio of} \enspace \frac{1}{3}\] \[\text{And} \enspace \frac{\text{length}}{\text{width}} = \frac{\text{0,8}\text{ m}}{\text{2,4}\text{ m}} \enspace \text{also gives a ratio of} \enspace \frac{1}{3}\]
• Do not convert a ratio to a decimal (even though \(\frac{1}{3}\) and \(\text{0,}\dot{3}\) have the same numerical value).

Proportion

Consider the diagram below:

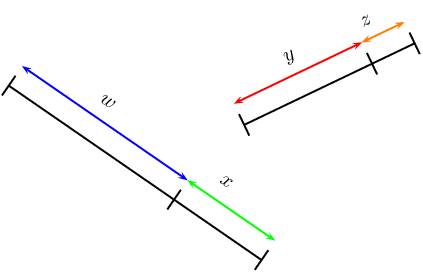
If two or more ratios are equal to each other, then we say that they are in the same proportion. Proportionality describes the equality of ratios.

If \(\dfrac{w}{x} = \dfrac{y}{z}\), then \(w\) and \(x\) are in the same proportion as \(y\) and \(z\).

1. \(wz = xy\)
2. \(\dfrac{x}{w} = \dfrac{z}{y}\)
3. \(\dfrac{w}{y} = \dfrac{x}{z}\)
4. \(\dfrac{y}{w} = \dfrac{z}{x}\)

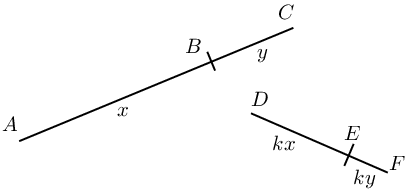
Given

The line segments \(AB\) and \(BC\) are in the same proportion as \(DE\) and \(EF\). The following statements are also true:

We can also substitute \(x\), \(y\), \(kx\), and \(ky\) to show algebraically that the statements are true.

For example,

Ratio and proportion

Textbook Exercise 8.2

Solve for \(p\):

\(\frac{8}{40} = \frac{p}{25}\)

\begin{align*} \frac{8}{40} &= \frac{p}{25} \\ \frac{8 \times 25}{40} &= p \\ \frac{200}{40} &= p \\ \therefore 5 &= p \end{align*}

\(\frac{6}{9} = \frac{29 + p}{54}\)

\begin{align*} \frac{6}{9} &= \frac{29 + p}{54} \\ \frac{6 \times 54}{9} &= 29 + p \\ 36 &= 29 + p \\ \therefore 7 &= p \end{align*}

\(\frac{3}{1 + \frac{p}{4}} = \frac{4}{p + 1}\)

\begin{align*} \frac{3}{1 + \frac{p}{4}} &= \frac{4}{p + 1} \\ 3(p + 1) &= 4 \left( 1 + \frac{p}{4} \right) \\ 3p + 3 &= 4 + p \\ 2p &= 1 \\ \therefore p &= \frac{1}{2} \end{align*}

\(\frac{14}{100 - p} = \frac{49}{343}\)

\begin{align*} \frac{14}{100 - p} &= \frac{49}{343} \\ 14 \times 343 &= 49( 100 - p) \\ \frac{4802}{49} &= 100 - p \\ 98 &= 100 - p \\ \therefore p &= 2 \end{align*}

A packet of \(\text{160}\) sweets contains red, blue and yellow sweets in the ratio of \(3:2:3\) respectively. Determine how many sweets of each colour there are in the packet.

\begin{align*} 3 + 2 + 3 &= 8 \\ \text{Red } &= \frac{3}{8} \times 160 \\ &= 60 \\ \text{Blue } &= \frac{2}{8} \times 160 \\ &= 40 \\ \text{Yellow } &= \frac{3}{8} \times 160 \\ &= 60 \end{align*}

A mixture contains \(\text{2}\) parts of substance \(A\) for every \(\text{5}\) parts of substance \(B\). If the total weight of the mixture is \(\text{50}\) \(\text{kg}\), determine how much of substance \(B\) is in the mixture (correct to \(\text{2}\) decimal places).

\begin{align*} \text{Ratio substance } A \text{ to substance B } &= 2 : 5 \\ 2 + 5 &= 7 \\ \text{Substance } B &= \frac{5}{7} \times 50 \\ &= \text{35,71}\text{ kg} \end{align*}

Given the diagram below.

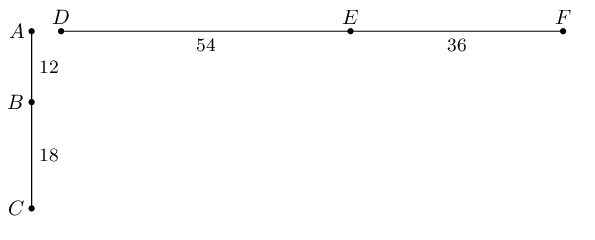
Show that:

\(\frac{AB}{BC} = \frac{FE}{ED}\)

\begin{align*} \frac{AB}{BC} &= \frac{12}{18} \\ &= \frac{2}{3} \\ \frac{FE}{ED} &= \frac{36}{54} \\ &= \frac{2}{3} \\ \therefore \frac{AB}{BC} &= \frac{FE}{ED} \end{align*}

\(\frac{AC}{BC} = \frac{FD}{EF}\)

\begin{align*} \frac{AC}{BC} &= \frac{12 + 18}{18} \\ &= \frac{30}{18} \\ &= \frac{5}{3} \\ \frac{FD}{EF} &= \frac{36 + 54}{54} \\ &= \frac{90}{54} \\ &= \frac{5}{3} \\ \therefore \frac{AC}{BC} &= \frac{FD}{EF} \end{align*}

\(AB \cdot DF = AC \cdot FE\)

\begin{align*} AB \cdot DF &= 12 \times (36 + 54) \\ &= 12 \times 90 \\ &= 1080 \\ AC \cdot FE &= (12 + 18) \times 36 \\ &= 30 \times 36 \\ &= 1080 \\ \therefore AB \cdot DF &= AC \cdot FE \end{align*}

Consider the line segment shown below.

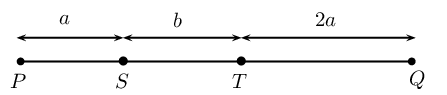
Express the following in terms of \(a\) and \(b\):

\(PT: ST\)

\((a + b): b\)

\(\frac{PS}{TQ}\)

\(\frac{a}{2a} = \frac{1}{2}\)

\(\frac{SQ}{PQ}\)

\(\frac{2a + b}{3a + b}\)

\(QT: TS\)

\(2a: b\)

\(ABCD\) is a parallelogram with \(DC = \text{15}\text{ cm}\), \(h = \text{8}\text{ cm}\) and \(BF = \text{9}\text{ cm}\).

Calculate the ratio \(\dfrac{\text{area } ABF}{\text{area } ABCD}\).

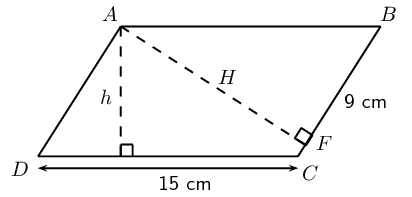
The area of a parallelogram \(ABCD =\) base \(\times\) height:

\begin{align*} \text{Area} &= \text{15} \times \text{8} \\ &= \text{120}\text{ cm$^{2}$} \end{align*}

The perimeter of a parallelogram \(ABCD = 2DC + 2BC\).

To find the length of \(AF\), we use \(AF \perp BC\) and the theorem of Pythagoras.

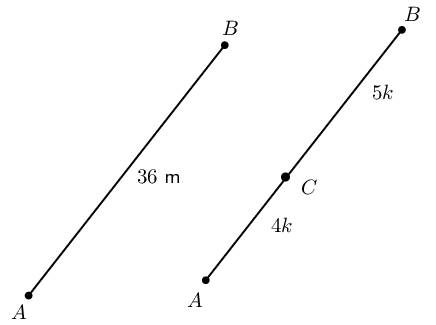
\begin{align*} \text{In \(\triangle ABF\):} \quad AF^2 &= AB^2 - BF^2 \\ &= \text{15}^2 - \text{9}^2 \\ &= \text{144} \\ \therefore AF &= \text{12}\text{ cm} \\ \therefore \text{area } ABF &= \frac{1}{2} AF \cdot BF \\ &= \frac{1}{2}(12)(9)\\ &= \text{54}\text{ cm} \end{align*} \begin{align*} \therefore \frac{\text{area } ABF}{\text{area } ABCD} &= \frac{54}{120} \\ &= \frac{9}{20} \end{align*}

\(AB = \text{36}\text{ m}\) and \(C\) divides \(AB\) in the ratio \(4:5\). Determine \(AC\) and \(CB\).

\begin{align*} \frac{AC}{AB} &= \frac{4k}{(4k + 5k)} \\ \therefore AC &= 36 \times \frac{4}{9} \\ &= \text{16}\text{ m} \\ CB &= 36 - 16 \\ &= \text{20}\text{ m} \\ \text{Or } \frac{CB}{AC} &= \frac{5k}{(4k + 5k)} \\ \therefore CB &= 36 \times \frac{5}{9} \\ &= \text{20}\text{ m} \end{align*}

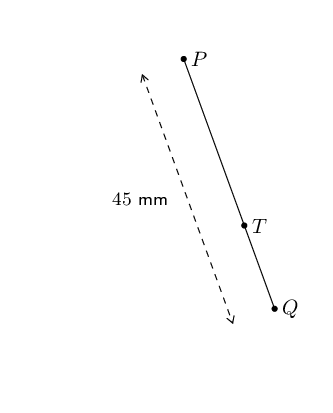
If \(PQ = \text{45}\text{ mm}\) and the ratio of \(TQ:PQ\) is \(2:3\), calculate \(PT\) and \(TQ\).

\begin{align*} \frac{TQ}{PQ} &= \frac{2}{3} \\ \therefore TQ &= PQ \times \frac{2}{3} \\ &= 45 \times \frac{2}{3} \\ &= \text{30}\text{ mm} \\ PT &= 45 - 30 \\ &= \text{15}\text{ mm} \\ \text{Or } \quad \frac{PT}{PQ} &= \frac{1}{3} \\ \therefore PT &= 45 \times \frac{1}{3} \\ &= \text{15}\text{ mm} \end{align*}

Luke's biology notebook is \(\text{30}\) \(\text{cm}\) long and \(\text{20}\) \(\text{cm}\) wide. The dimensions of his desk are in the same proportion as the dimensions of his notebook.

If the desk is \(\text{90}\text{ cm}\) wide, calculate the area of the top of the desk.

\begin{align*} \text{Ratio } &= \frac{\text{table width}}{\text{book width}} \\ &=\frac{90}{20} \\ &=\text{4,5} \\ \therefore \text{Length of table } &= 30 \times \text{4,5} \text{cm} \\ &=\text{135}\text{ cm}\\ \text{Area table} &= 135 \times 90 \\ &=\text{12 150}\text{ cm$^{2}$}\\ &=\text{1,2}\text{ m$^{2}$} \end{align*}

Luke covers each corner of his desk with an isosceles triangle of cardboard, as shown in the diagram:

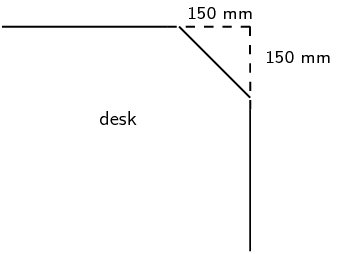
Calculate the new perimeter and area of the visible part of the top of his desk.

\begin{align*} x^2&=15^2+15^2 \\ x&=\text{21,2}\text{ cm}\\ \text{New length}&=135-2(15) \\ &=\text{105}\text{ cm} \\ \text{New breadth}&=90-2(15) \\ &=\text{60}\text{ cm}\\ \text{New perimeter }&=2(105)+2(60)+4(\text{21,2})\\ &=\text{414,8}\text{ cm} \end{align*} \begin{align*} \text{Area cut off}&=2\times(15^2) \\ &=\text{450}\text{ m$^{2}$} \\ \text{New area } &= \text{12 150}\text{ cm$^{2}$} - \text{450}\text{ m$^{2}$} \\ &= \text{11 700}\text{ cm$^{2}$} \end{align*}

Use this new area to calculate the dimensions of a square desk with the same desk top area.

\begin{align*} s^2&= \text{11 700}\text{ cm$^{2}$} \\ \therefore s&= \text{108,2}\text{ cm}\\ \text{Square table of length} &\approx 108 \times 108 \text{cm$^{2}$} \end{align*}