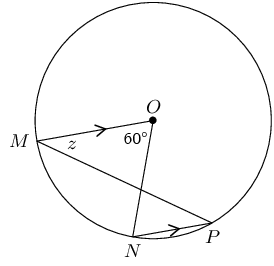
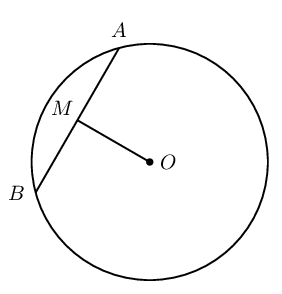
\(MO \parallel NP\) in a circle with centre \(O\). \(M\hat{O}N = \text{60}°\) and \(O\hat{M}P = z\). Calculate the value of \(z\), giving reasons.
|
Previous
End of chapter exercises
|
Next
8.2 Ratio and proportion
|
|
Name |
Diagram |
Properties |
|
Scalene |
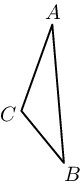 |
All sides and angles are different. |
|
Isosceles |
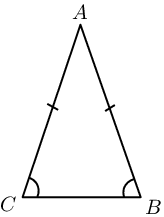 |
Two sides are equal in length. The angles opposite the equal sides are also equal. |
|
Equilateral |
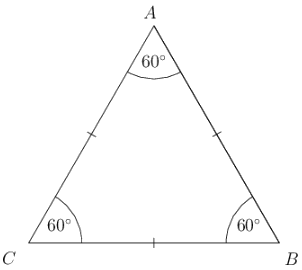 |
All three sides are equal in length and all three angles are equal. |
|
Acute-angled |
 |
Each of the three interior angles is less than \(\text{90}\)°. |
|
Obtuse-angled |
 |
One interior angle is greater than \(\text{90}\)°. |
|
Right-angled |
 |
One interior angle is \(\text{90}\)°. |
|
Condition |
Diagram |
|
SSS (side, side, side) |
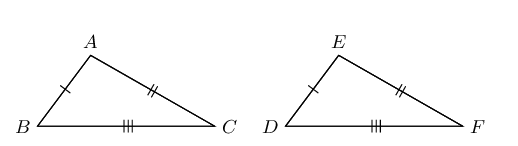
\(\triangle ABC \equiv \triangle EDF\) |
|
SAS (side, incl. angle, side) |
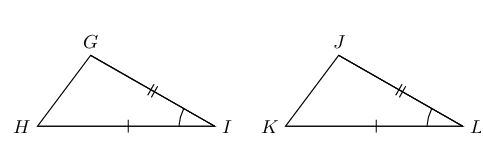
\(\triangle GHI \equiv \triangle JKL\) |
|
AAS (angle, angle, side) |

\(\triangle MNO \equiv \triangle PQR\) |
|
RHS (\(\text{90}\)°, hypotenuse, side) |
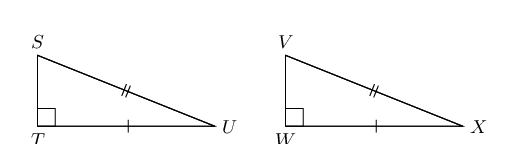
\(\triangle STU \equiv \triangle VWX\) |
|
Condition |
Diagram |
|
AAA (angle, angle, angle) |
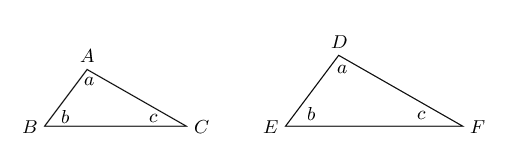
\(\hat{A} = \hat{D}, \enspace \hat{B} = \hat{E}, \enspace \hat{C} = \hat{F}\) \(\therefore \triangle ABC \enspace ||| \enspace \triangle DEF\) |
|
SSS (sides in prop.) |
\(\frac{MN}{RS} = \frac{ML}{RT} = \frac{NL}{ST}\) \(\therefore \triangle MNL \enspace ||| \enspace \triangle RST\) |
 |
|
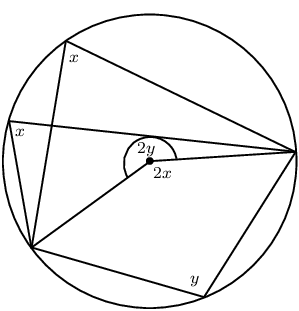 |
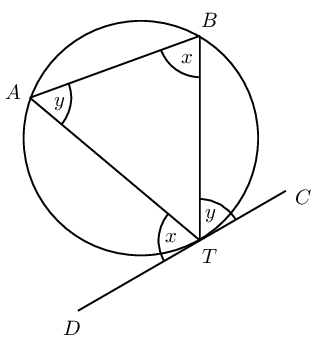
If an arc subtends an angle at the centre of a circle and at the circumference, then the angle at the centre is twice the size of the angle at the circumference. |
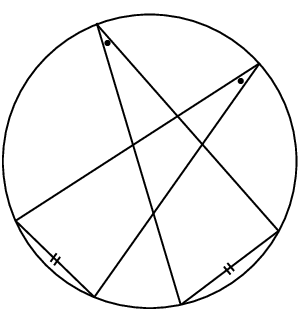 |
Angles at the circumference subtended by arcs of equal length (or by the same arc) are equal. |
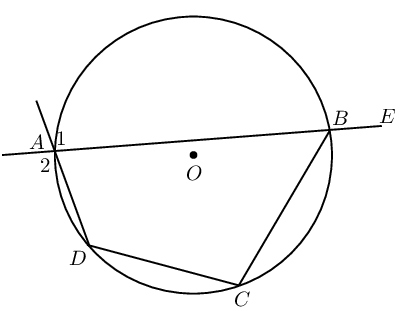 |
If the four sides of a quadrilateral \(ABCD\) are the chords of a circle with centre \(O\), then:
|
Proving a quadrilateral is cyclic:
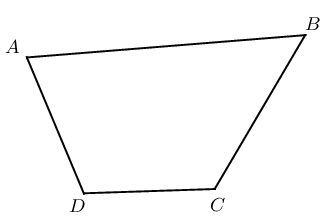 |
If \(\hat{A} + \hat{C} = \text{180}°\) or \(\hat{B} + \hat{D} = \text{180}°\), then \(ABCD\) is a cyclic quadrilateral. |
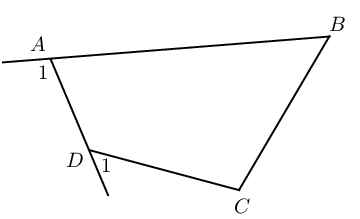 |
If \(\hat{A}_1 = \hat{C}\) or \(\hat{D}_1 = \hat{B}\), then \(ABCD\) is a cyclic quadrilateral. |
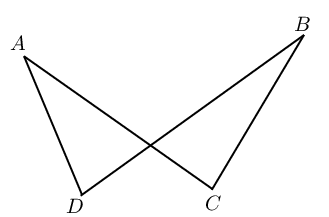 |
If \(\hat{A} = \hat{B}\) or \(\hat{C} = \hat{D}\), then \(ABCD\) is a cyclic quadrilateral. |
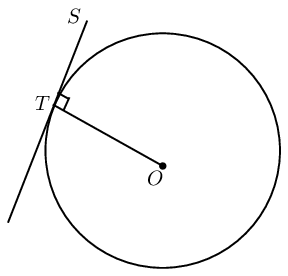 |
A tangent is perpendicular to the radius (\(OT \perp ST\)), drawn to the point of contact with the circle. |
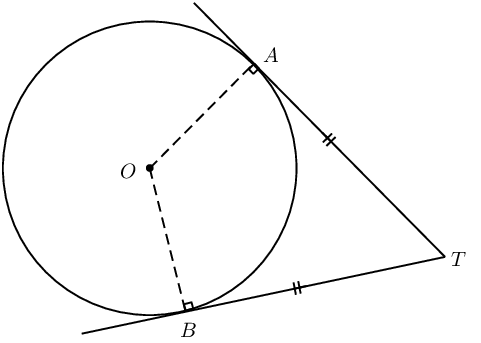 |
If \(AT\) and \(BT\) are tangents to a circle with centre \(O\), then:
|
 |
|
The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the length of the third side.
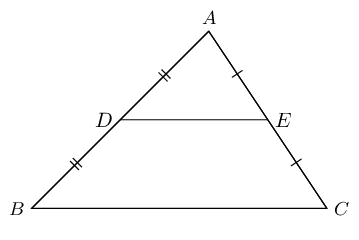
Given: \(AD = DB\) and \(AE = EC\), we can conclude that \(DE \parallel BC\) and \(DE = \frac{1}{2}BC\).
\(MO \parallel NP\) in a circle with centre \(O\). \(M\hat{O}N = \text{60}°\) and \(O\hat{M}P = z\). Calculate the value of \(z\), giving reasons.

\(O\) is the centre of the circle with \(OC = \text{5}\text{ cm}\) and chord \(BC = \text{8}\text{ cm}\).
Determine the lengths of:
\(PQ\) is a diameter of the circle with centre \(O\). \(SQ\) bisects \(P\hat{Q}R\) and \(P\hat{Q}S = a\).
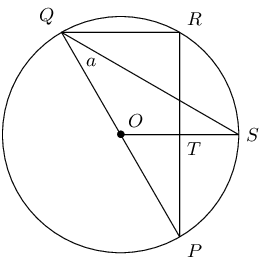
Write down two other angles that are also equal to \(a\).
Calculate \(P\hat{O}S\) in terms of \(a\), giving reasons.
Prove that \(OS\) is a perpendicular bisector of \(PR\).
\(BD\) is a diameter of the circle with centre \(O\). \(AB = AD\) and \(O\hat{C}D = \text{35}°\).
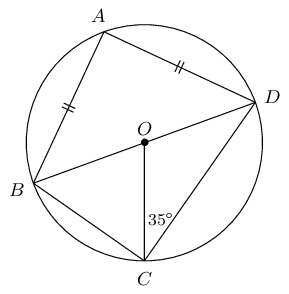
Calculate the value of the following angles, giving reasons:
\(O\) is the centre of the circle with diameter \(AB\). \(CD \perp AB\) at \(P\) and chord \(DE\) intersects \(AB\) at \(F\).
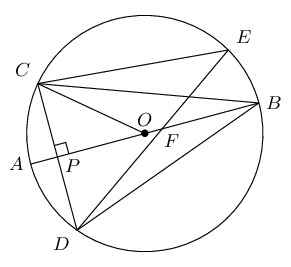
Prove the following:
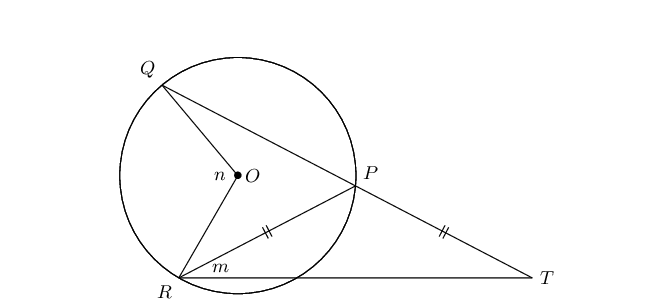
\(QP\) in the circle with centre \(O\) is extended to \(T\) so that \(PR = PT\). Express \(m\) in terms of \(n\).
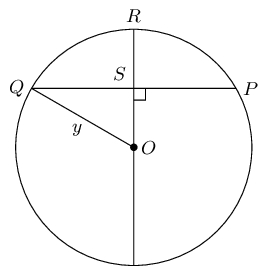
In the circle with centre \(O\), \(OR \perp QP\), \(QP = \text{30}\text{ mm}\) and \(RS = \text{9}\text{ mm}\). Determine the length of \(y\).
\(PQ\) is a diameter of the circle with centre \(O\). \(QP\) is extended to \(A\) and \(AC\) is a tangent to the circle. \(BA \perp AQ\) and \(BCQ\) is a straight line.
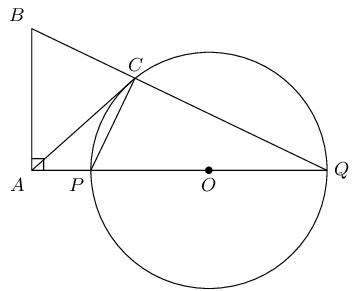
Prove the following:
\(BAPC\) is a cyclic quadrilateral
\(TA\) and \(TB\) are tangents to the circle with centre \(O\). \(C\) is a point on the circumference and \(A\hat{T}B = x\).
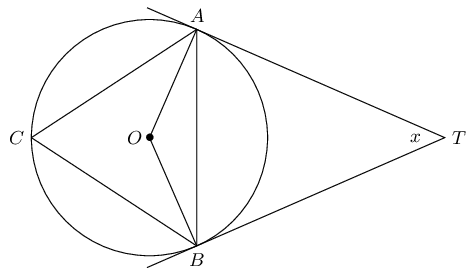
Express the following in terms of \(x\), giving reasons:
|
Previous
End of chapter exercises
|
Table of Contents |
Next
8.2 Ratio and proportion
|