In the circle with centre \(O\), \(OQ \perp PR\), \(OQ = 4\) units and \(PR=10\). Determine \(x\).
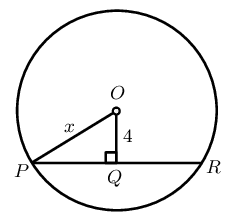
|
Previous
8.1 Revision
|
Next
8.3 Summary
|
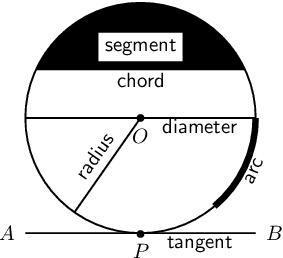
Terminology
The following terms are regularly used when referring to circles:
Axioms
An axiom is an established or accepted principle. For this section, the following are accepted as axioms.
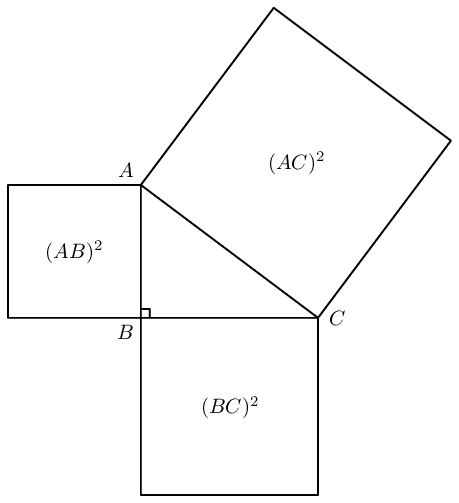
The theorem of Pythagoras states that the square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides.
\[(AC)^2 = (AB)^2 + (BC)^2\]
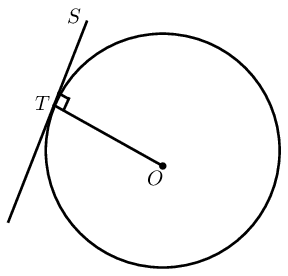
A tangent is perpendicular to the radius (\(OT \perp ST\)), drawn at the point of contact with the circle.
A theorem is a hypothesis (proposition) that can be shown to be true by accepted mathematical operations and arguments. A proof is the process of showing a theorem to be correct.
The converse of a theorem is the reverse of the hypothesis and the conclusion. For example, given the theorem “if \(A\), then \(B\)”, the converse is “if \(B\), then \(A\)”.
If a line is drawn from the centre of a circle perpendicular to a chord, then it bisects the chord.
(Reason: \(\perp\) from centre bisects chord)
Circle with centre \(O\) and line \(OP\) perpendicular to chord \(AB\).
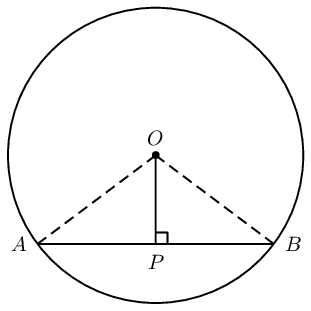
Draw \(OA\) and \(OB\).
In \(\triangle OPA\) and in \(\triangle OPB\), \[\begin{array}{rll} OA^2 &= OP^2 + AP^2 & \text{(Pythagoras)} \\ OB^2 &= OP^2 + BP^2 & \text{(Pythagoras)} \end{array}\] and \[\begin{array}{rll} OA &= OB & \text{(equal radii)} \\ \therefore AP^2 &= BP^2 & \\ \therefore AP &= BP & \end{array}\] Therefore \(OP\) bisects \(AB\).
Alternative proof:
In \(\triangle OPA\) and in \(\triangle OPB\), \[\begin{array}{rll} O\hat{P}A &= O\hat{P}B & (\text{given } OP \perp AB) \\ OA &= OB & \text{(equal radii)} \\ OP &= OP & \text{(common side)} \\ \therefore \triangle OPA & \equiv \triangle OPB & \text{(RHS)} \\ \therefore AP &= PB & \end{array}\] Therefore \(OP\) bisects \(AB\).
If a line is drawn from the centre of a circle to the mid-point of a chord, then the line is perpendicular to the chord.
(Reason: line from centre to mid-point \(\perp\))
Circle with centre \(O\) and line \(OP\) to mid-point \(P\) on chord \(AB\).
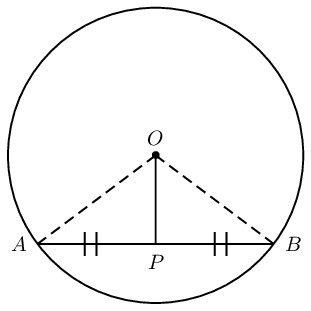
Draw \(OA\) and \(OB\).
In \(\triangle OPA\) and in \(\triangle OPB\), \[\begin{array}{rll} OA &= OB & \text{(equal radii)} \\ AP &= PB & \text{(given)} \\ OP &= OP & \text{(common side)} \\ \therefore \triangle OPA & \equiv \triangle OPB & \text{(SSS)} \\ \therefore O\hat{P}A &= O\hat{P}B & \\ \text{and } O\hat{P}A + O\hat{P}B &= \text{180}\text{°} & (\angle \text{ on str. line}) \\ \therefore O\hat{P}A = O\hat{P}B &= \text{90}\text{°} & \end{array}\] Therefore \(OP \perp AB\).
If the perpendicular bisector of a chord is drawn, then the line will pass through the centre of the circle.
(Reason: \(\perp\) bisector through centre)
Circle with mid-point \(P\) on chord \(AB\).
Line \(QP\) is drawn such that \(Q\hat{P}A = Q\hat{P}B = \text{90}\text{°}\).
Line \(RP\) is drawn such that \(R\hat{P}A = R\hat{P}B = \text{90}\text{°}\).
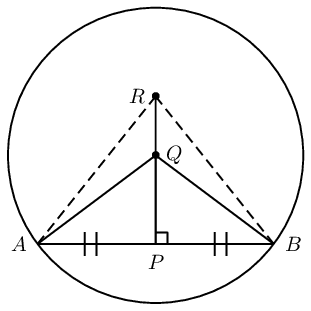
Draw lines \(QA\) and \(QB\).
Draw lines \(RA\) and \(RB\).
In \(\triangle QPA\) and in \(\triangle QPB\), \[\begin{array}{rll} AP &= PB & \text{(given)} \\ QP &= QP & \text{(common side)} \\ Q\hat{P}A = Q\hat{P}B &= \text{90}\text{°} & \text{(given)} \\ \therefore \triangle QPA & \equiv \triangle QPB & \text{(SAS)} \\ \therefore QA &= QB & \end{array}\]
Similarly it can be shown that in \(\triangle RPA\) and in \(\triangle RPB\), \(RA = RB\).
We conclude that all the points that are equidistant from \(A\) and \(B\) will lie on the line \(PR\) extended. Therefore the centre \(O\), which is equidistant to all points on the circumference, must also lie on the line \(PR\).
Given \(OQ \perp PR\) and \(PR = 8\) units, determine the value of \(x\).
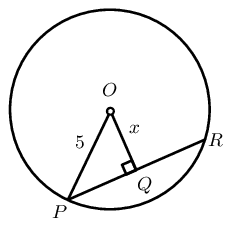
\(PQ = QR = 4 \qquad (\perp \text{ from centre bisects chord})\)
In \(\triangle OQP\): \[\begin{array}{rll} PQ &= 4 & (\perp \text{ from centre bisects chord}) \\ OP^2 &= OQ^2 + QP^2 & (\text{Pythagoras}) \\ 5^2 &= x^2 + 4^2 & \\ \therefore x^2 &= 25 - 16 & \\ x^2 &= 9 & \\ x &= 3 & \end{array}\]
\(x = 3\) units.
In the circle with centre \(O\), \(OQ \perp PR\), \(OQ = 4\) units and \(PR=10\). Determine \(x\).
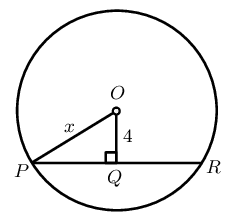
In the circle with centre \(O\) and radius \(= 10\) units, \(OQ \perp PR\) and \(PR=8\). Determine \(x\).
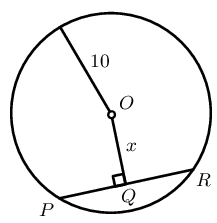
In the circle with centre \(O\), \(OQ \perp PR\), \(PR = 12\) units and \(SQ = 2\) units. Determine \(x\).
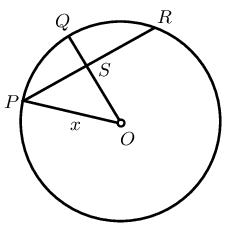
In the circle with centre \(O\), \(OT \perp SQ\), \(OT \perp PR\), \(OP = 10\) units, \(ST = 5\) units and \(PU = 8\) units. Determine \(TU\).
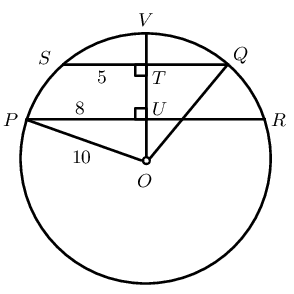
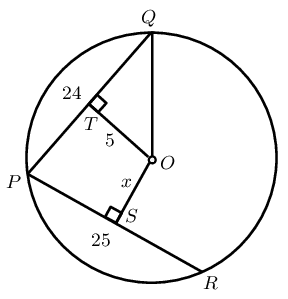
In the circle with centre \(O\), \(OT \perp QP\), \(OS \perp PR\), \(OT = 5\) units, \(PQ = 24\) units and \(PR = 25\) units. Determine \(OS = x\).
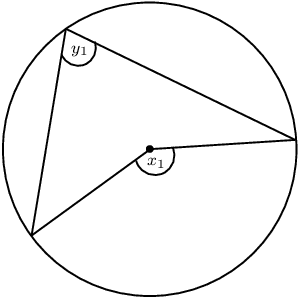
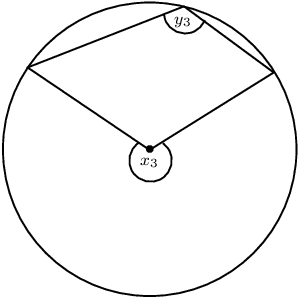
Measure angles \(x\) and \(y\) in each of the following graphs:
|

|
|
Complete the table:
| \(x\) | \(y\) |
If an arc subtends an angle at the centre of a circle and at the circumference, then the angle at the centre is twice the size of the angle at the circumference.
(Reason: \(\angle \text{ at centre } = 2 \angle \text{ at circum.}\))
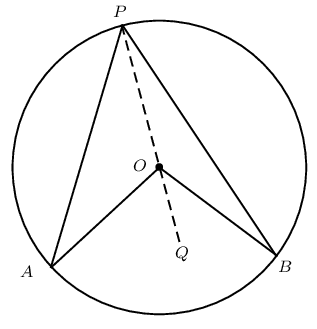
Circle with centre \(O\), arc \(AB\) subtending \(A\hat{O}B\) at the centre of the circle, and \(A\hat{P}B\) at the circumference.
|
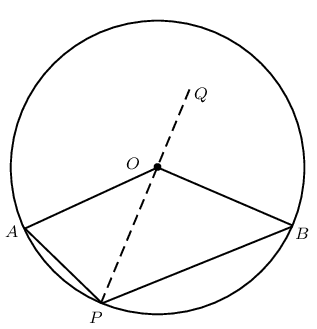
|
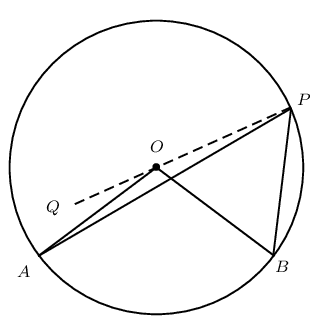
|
Draw \(PO\) extended to \(Q\) and let \(A\hat{O}Q = \hat{O}_1\) and \(B\hat{O}Q = \hat{O}_2\).
\[\begin{array}{rll} \hat{O}_1&= A\hat{P}O + P\hat{A}O & (\text{ext. } \angle \triangle = \text{sum int. opp. } \angle \text{s} ) \\ \text{and } A\hat{P}O &= P\hat{A}O & (\text{equal radii, isosceles } \triangle APO)\\ \therefore \hat{O}_1&= A\hat{P}O + A\hat{P}O & \\ \hat{O}_1&= 2A\hat{P}O & \end{array}\]Similarly, we can also show that \(\hat{O}_2 = 2B\hat{P}O\).
For the first two diagrams shown above we have that: \[\begin{array}{rll} A\hat{O}B &= \hat{O}_1 + \hat{O}_2 & \\ &= 2A\hat{P}O + 2B\hat{P}O & \\ &= 2(A\hat{P}O + B\hat{P}O) & \\ \therefore A\hat{O}B &= 2(A\hat{P}B) & \end{array}\] And for the last diagram: \[\begin{array}{rll} A\hat{O}B &= \hat{O}_2 - \hat{O}_1 & \\ &= 2B\hat{P}O - 2A\hat{P}O & \\ &= 2(B\hat{P}O - A\hat{P}O) & \\ \therefore A\hat{O}B &= 2(A\hat{P}B) & \end{array}\]
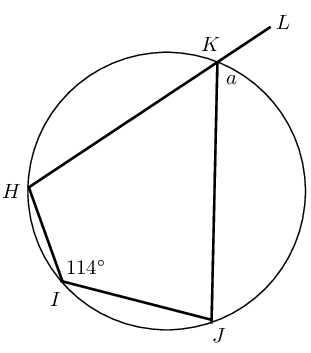
Given \(HK\), the diameter of the circle passing through centre \(O\).
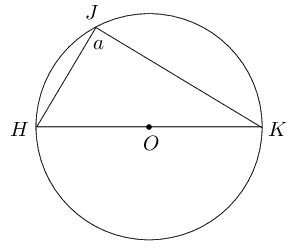
In \(\triangle HJK\): \[\begin{array}{rll} H\hat{O}K &= \text{180}\text{°} & (\angle \text{ on str. line)} \\ &= 2a & (\angle \text{ at centre } = 2 \angle \text{ at circum.}) \\ \therefore 2a &= \text{180}\text{°} & \\ a &= \frac{\text{180}\text{°}}{2} & \\ &= \text{90}\text{°} & \end{array}\]
The diameter of a circle subtends a right angle at the circumference (angles in a semi-circle).
Given \(O\) is the centre of the circle, determine the unknown angle in each of the following diagrams:
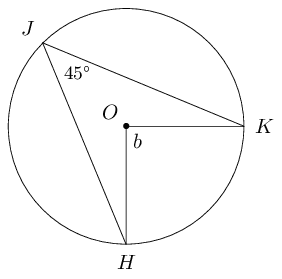
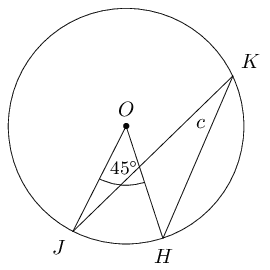
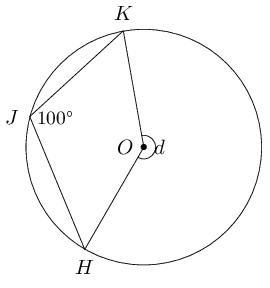
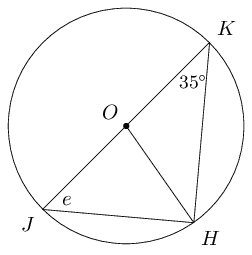
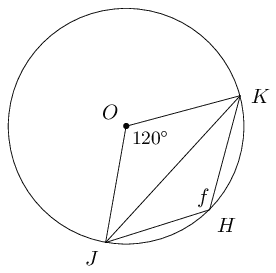
Measure angles \(a\), \(b\), \(c\), \(d\) and \(e\) in the diagram below:

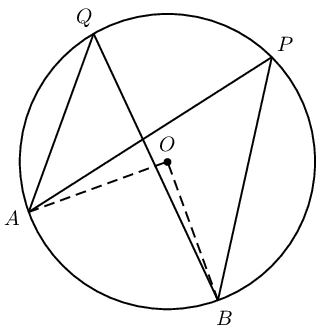
Choose any two points on the circumference of the circle and label them \(A\) and \(B\).
Draw \(AP\) and \(BP\), and measure \(A\hat{P}B\).
Draw \(AQ\) and \(BQ\), and measure \(A\hat{Q}B\).
If the angles subtended by a chord of the circle are on the same side of the chord, then the angles are equal.
(Reason: \(\angle\)s in same seg.)
Circle with centre \(O\), and points \(P\) and \(Q\) on the circumference of the circle. Arc \(AB\) subtends \(A\hat{P}B\) and \(A\hat{Q}B\) in the same segment of the circle.
Equal arcs subtend equal angles
From the theorem above we can deduce that if angles at the circumference of a circle are subtended by arcs of equal length, then the angles are equal. In the figure below, notice that if we were to move the two chords with equal length closer to each other, until they overlap, we would have the same situation as with the theorem above. This shows that the angles subtended by arcs of equal length are also equal.

If a line segment subtends equal angles at two other points on the same side of the line segment, then these four points are concyclic (lie on a circle).
Line segment \(AB\) subtending equal angles at points \(P\) and \(Q\) on the same side of the line segment \(AB\).

\(A\), \(B\), \(P\) and \(Q\) lie on a circle.
Proof by contradiction:
Points on the circumference of a circle: we know that there are only two possible options regarding a given point — it either lies on circumference or it does not.
We will assume that point \(P\) does not lie on the circumference.
We draw a circle that cuts \(AP\) at \(R\) and passes through \(A\), \(B\) and \(Q\). \[\begin{array}{rll} A\hat{Q}B &= A\hat{R}B & (\angle \text{s in same seg.}) \\ \text{but } A\hat{Q}B &= A\hat{P}B & (\text{given}) \\ \therefore A\hat{R}B &= A\hat{P}B & \\ \text{but } A\hat{R}B &= A\hat{P}B + R\hat{B}P & (\text{ext. } \angle \triangle = \text{sum int. opp.}) \\ \therefore R\hat{B}P &= \text{0}\text{°} & \end{array}\] Therefore the assumption that the circle does not pass through \(P\) must be false.
We can conclude that \(A\), \(B\), \(Q\) and \(P\) lie on a circle (\(A\), \(B\), \(Q\) and \(P\) are concyclic).
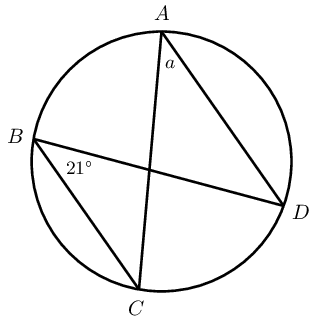
Given \(FH \parallel EI\) and \(E\hat{I}F = \text{15}\text{°}\), determine the value of \(b\).

Find the values of the unknown angles.
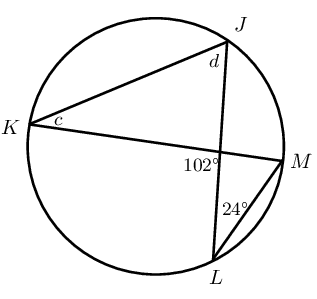
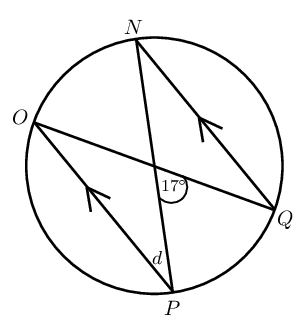

Given \(T\hat{V}S = S\hat{V}R\), determine the value of \(e\).
Is \(TV\) a diameter of the circle? Explain your answer.
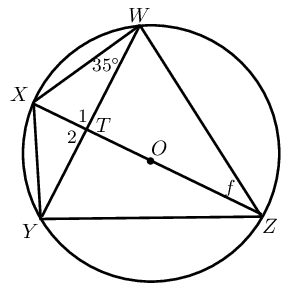
Given circle with centre \(O\), \(WT = TY\) and \(X\hat{W}T = \text{35}\text{°}\). Determine \(f\).
Cyclic quadrilaterals
Cyclic quadrilaterals are quadrilaterals with all four vertices lying on the circumference of a circle (concyclic).
Consider the diagrams given below:
| Circle \(\text{1}\) | Circle \(\text{2}\) | Circle \(\text{3}\) |
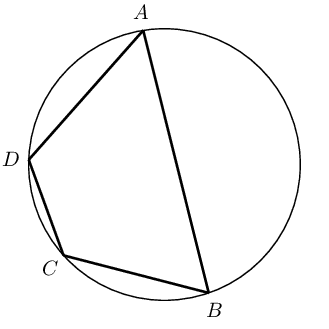
|
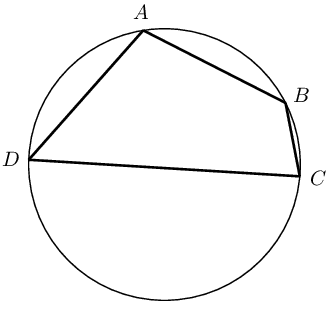
|
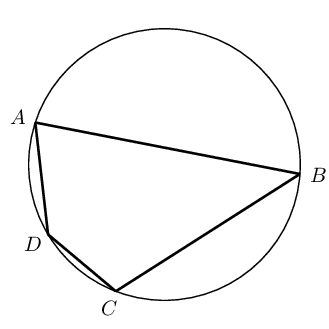
|
Complete the following:
\(ABCD\) is a cyclic quadrilateral because \(\ldots \ldots\)
Complete the table:
| Circle \(\text{1}\) | Circle \(\text{2}\) | Circle \(\text{3}\) | |
| \(\hat{A} =\) | |||
| \(\hat{B} =\) | |||
| \(\hat{C} =\) | |||
| \(\hat{D} =\) | |||
| \(\hat{A} + \hat{C} =\) | |||
| \(\hat{B} + \hat{D} =\) |
The opposite angles of a cyclic quadrilateral are supplementary.
(Reason: opp. \(\angle\)s cyclic quad.)
Circle with centre \(O\) with points \(A, B, P\) and \(Q\) on the circumference such that \(ABPQ\) is a cyclic quadrilateral.
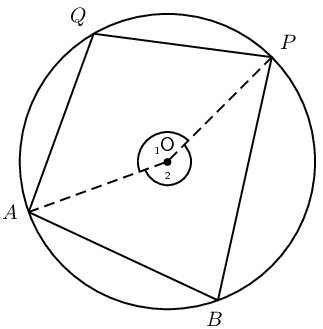
\(A\hat{B}P + A\hat{Q}P = \text{180}\text{°}\) and \(Q\hat{A}B + Q\hat{P}B = \text{180}\text{°}\)
Draw \(AO\) and \(OP\). Label \(\hat{O}_1\) and \(\hat{O}_2\). \[\begin{array}{rll} \hat{O}_1 &= 2A\hat{B}P & (\angle\text{ at centre} = 2\angle \text{ at circum.})\\ \hat{O}_2 &= 2A\hat{Q}P & (\angle\text{ at centre} = 2\angle \text{ at circum.})\\ \text{and } \hat{O}_1 + \hat{O}_2 &= \text{360}\text{°} & (\angle\text{s around a point}) \\ \therefore 2A\hat{B}P + 2A\hat{Q}P &= \text{360}\text{°} & \\ A\hat{B}P + A\hat{Q}P &= \text{180}\text{°} & \end{array}\] Similarly, we can show that \(Q\hat{A}B + Q\hat{P}B = \text{180}\text{°}\).
Converse: interior opposite angles of a quadrilateral
If the interior opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
Exterior angle of a cyclic quadrilateral
If a quadrilateral is cyclic, then the exterior angle is equal to the interior opposite angle.
Given the circle with centre \(O\) and cyclic quadrilateral \(PQRS\). \(SQ\) is drawn and \(S\hat{P}Q = \text{34}\text{°}\). Determine the values of \(a\), \(b\) and \(c\).
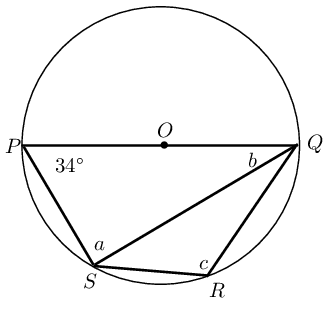
\[\begin{array}{rll} S\hat{P}Q + c &= \text{180}\text{°} & (\text{opp. } \angle \text{s cyclic quad supp.}) \\ \therefore c &= \text{180}\text{°} - \text{34}\text{°} & \\ &= \text{146}\text{°} & \end{array}\] \[\begin{array}{rll} a &= \text{90}\text{°} & (\angle \text{ in semi circle}) \end{array}\] In \(\triangle PSQ\): \[\begin{array}{rll} a + b + \text{34}\text{°} &= \text{180}\text{°} & (\angle \text{ sum of } \triangle) \\ \therefore b &= \text{180}\text{°} - \text{90}\text{°} - \text{34}\text{°} & \\ &= \text{56}\text{°} & \end{array}\]
Methods for proving a quadrilateral is cyclic
There are three ways to prove that a quadrilateral is a cyclic quadrilateral:
| Method of proof | Reason | |
 |
If \(\hat{P} + \hat{R} = \text{180}\text{°}\) or \(\hat{S} + \hat{Q} = \text{180}\text{°}\), then \(PQRS\) is a cyclic quad. | opp. int. angles suppl. |
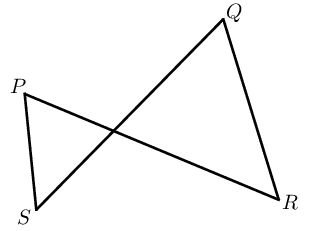 |
If \(\hat{P} = \hat{Q}\) or \(\hat{S} = \hat{R}\), then \(PQRS\) is a cyclic quad. | angles in the same seg. |
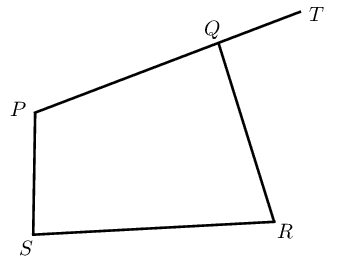 |
If \(T\hat{Q}R = \hat{S}\), then \(PQRS\) is a cyclic quad. | ext. angle equal to int. opp. angle |
Prove that \(ABDE\) is a cyclic quadrilateral.
Find the values of the unknown angles.
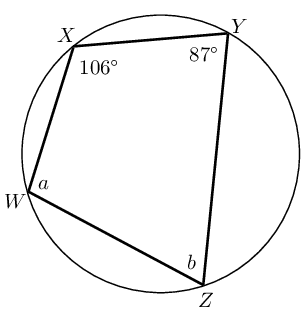
Prove that \(ABCD\) is a cyclic quadrilateral:
Tangent line to a circle
A tangent is a line that touches the circumference of a circle at only one place. The radius of a circle is perpendicular to the tangent at the point of contact.

If two tangents are drawn from the same point outside a circle, then they are equal in length.
(Reason: tangents from same point equal)
Circle with centre \(O\) and tangents \(PA\) and \(PB\), where \(A\) and \(B\) are the respective points of contact for the two lines.
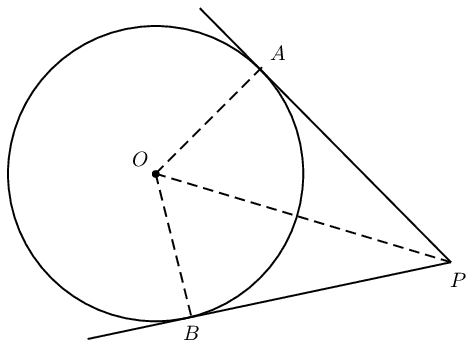
\(AP = BP\)
In \(\triangle AOP\) and \(\triangle BOP\), \[\begin{array}{rll} O\hat{A}P = O\hat{B}P &= \text{90}\text{°} & (\text{tangent} \perp \text{radius})\\ AO &= BO & (\text{equal radii}) \\ OP &= OP & (\text{common side}) \\ \therefore \triangle AOP &\equiv \triangle BOP & (\text{RHS}) \\ \therefore AP &= BP & \end{array}\]
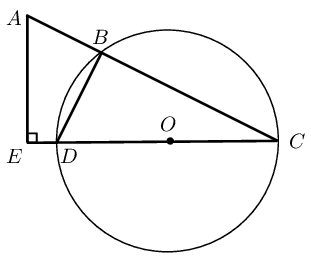
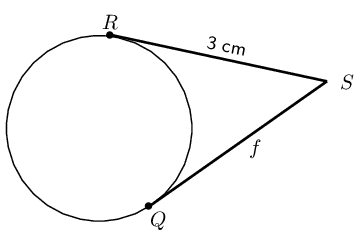
In the diagram below \(AE = \text{5}\text{ cm}\), \(AC = \text{8}\text{ cm}\) and \(CE = \text{9}\text{ cm}\). Determine the values of \(a\), \(b\) and \(c\).
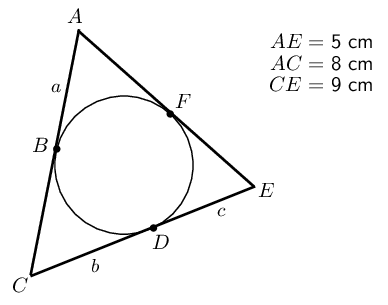
Subtract equation \((1)\) from equation \((2)\) and then substitute into equation \((3)\):
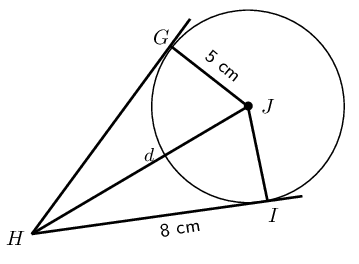
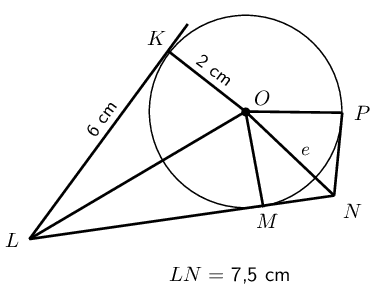
\[\begin{array}{rll} (2) - (1) \quad b-c &= 8-5 & \\ &= 3 & \\ \therefore b &= c + 3 & \\ \text{Substitute into } (3) \quad c + 3 + c &= 9 & \\ 2c &= 6 & \\ c &= 3 & \\ \therefore a &= 2 & \\ \text{ and } b &= 6 & \end{array}\]Find the values of the unknown lengths.
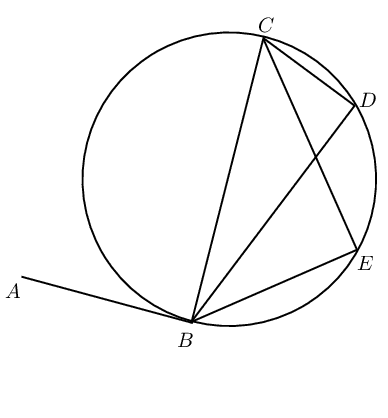
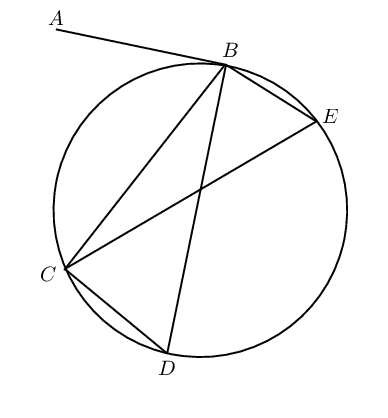
Consider the diagrams given below:
| Diagram \(\text{1}\) | Diagram \(\text{2}\) | Diagram \(\text{3}\) |
|
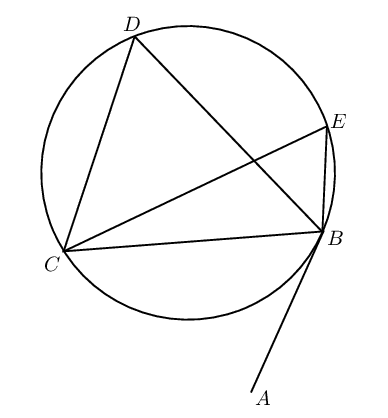
|
|
Measure the following angles with a protractor and complete the table:
| Diagram \(\text{1}\) | Diagram \(\text{2}\) | Diagram \(\text{3}\) | |
| \(A\hat{B}C =\) | |||
| \(\hat{D} =\) | |||
| \(\hat{E} =\) |
The angle between a tangent to a circle and a chord drawn at the point of contact, is equal to the angle which the chord subtends in the alternate segment.
(Reason: tan. chord theorem)
Circle with centre \(O\) and tangent \(SR\) touching the circle at \(B\). Chord \(AB\) subtends \(\hat{P}_1\) and \(\hat{Q}_1\).
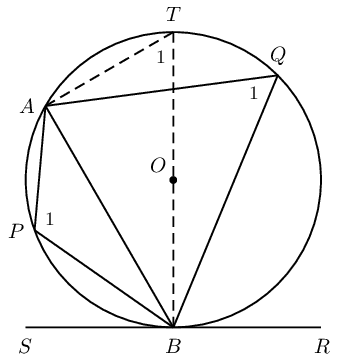
Draw diameter \(BT\) and join \(T\) to \(A\).
Let \(A\hat{T}B = T_1\). \[\begin{array}{rll} A\hat{B}S + A\hat{B}T &= \text{90}\text{°} & (\text{tangent} \perp \text{radius}) \\ B\hat{A}T &= \text{90}\text{°} & (\angle \text{ in semi circle}) \\ \therefore A\hat{B}T + T_1 &= \text{90}\text{°} & (\angle \text{ sum of } \triangle BAT) \\ \therefore A\hat{B}S &= T_1 & \\ \text{but } Q_1 &= T_1 & (\angle \text{s in same segment}) \\ \therefore Q_1 &= A\hat{B}S & \end{array}\] \[\begin{array}{rll} A\hat{B}S + A\hat{B}R &= \text{180}\text{°} & (\angle \text{s on str. line}) \\ \hat{Q}_1 + \hat{P}_1 &= \text{180}\text{°} & (\text{opp. } \angle \text{s cyclic quad. supp.}) \\ \therefore A\hat{B}S + A\hat{B}R &= Q_1 + P_1 & \\ \text{and } A\hat{B}S &= Q_1 & \\ \therefore A\hat{B}R &= P_1 & \end{array}\]
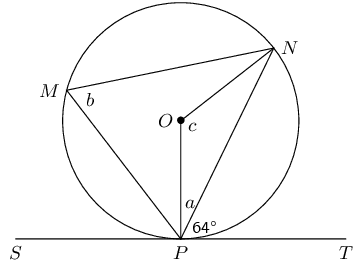
Determine the values of \(h\) and \(s\).
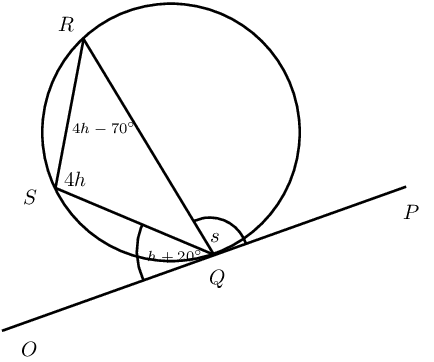
Find the values of the unknown letters, stating reasons.
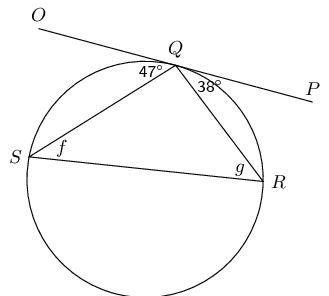
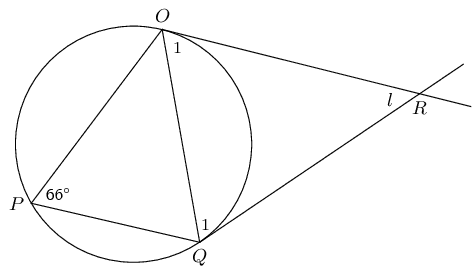
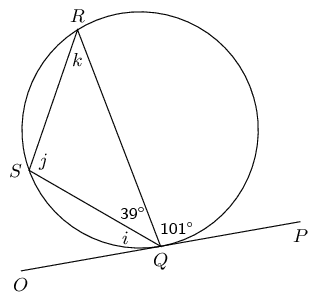
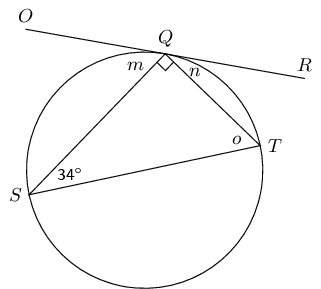
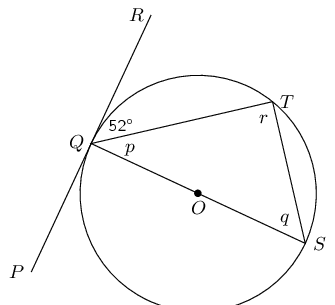
\(O\) is the centre of the circle and \(SPT\) is a tangent, with \(OP \perp ST\). Determine \(a\), \(b\) and \(c\), giving reasons.
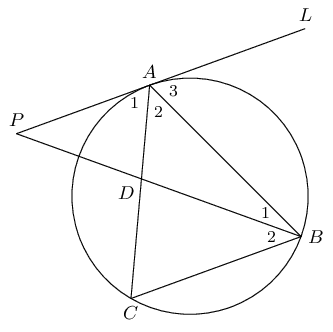
Given \(AB = AC\), \(AP \parallel BC\) and \(\hat{A}_2 = \hat{B}_2\). Prove:
\(PAL\) is a tangent to the circle \(ABC\).
\(AB\) is a tangent to the circle \(ADP\).
Converse: tangent-chord theorem
If a line drawn through the end point of a chord forms an angle equal to the angle subtended by the chord in the alternate segment, then the line is a tangent to the circle.
(Reason: \(\angle\) between line and chord \(= \angle\) in alt. seg. )
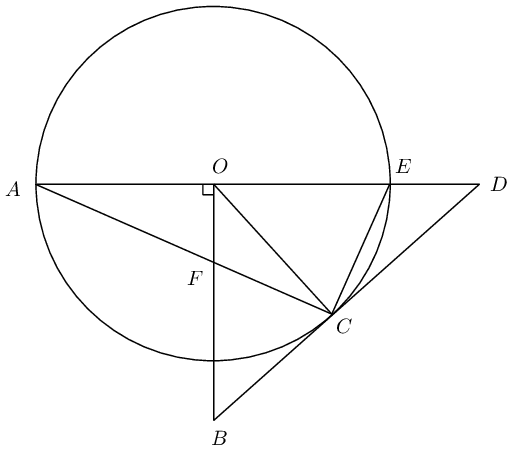
\(BD\) is a tangent to the circle with centre \(O\), with \(BO \perp AD\).
Prove that:
\(CFOE\) is a cyclic quadrilateral
\(FB=BC\)
\(\angle A\hat{O}C = 2 B\hat{F}C\)
Will \(DC\) be a tangent to the circle passing through \(C,F,O\) and \(E\)? Motivate your answer.
To show that \(FB = BC\) we first prove \(\triangle BFC\) is an isosceles triangle by showing that \(B\hat{F}C = B\hat{C}F\).
\[\begin{array}{rll} B\hat{C}F &= C\hat{E}O & (\text{tangent-chord}) \\ C\hat{E}O &= B\hat{F}C & (\text{ext. } \angle \text{ cyclic quad. } CFOE) \\ \therefore B\hat{F}C &= B\hat{C}F \\ \therefore FB &= BC & (\triangle BFC \text{ isosceles}) \end{array}\]Proof by contradiction.
Let us assume that \(DC\) is a tangent to the circle passing through the points \(C\), \(F\), \(O\) and \(E\): \[\begin{array}{rll} \therefore D\hat{C}E = C\hat{O}E \quad (\text{tangent-chord}) \end{array}\] And using the circle with centre \(O\) and tangent \(BD\) we have that: \[\begin{array}{rll} D\hat{C}E &= C\hat{A}E & (\text{tangent-chord}) \\ \text{but } C\hat{A}E &= \frac{1}{2} C\hat{O}E & (\angle \text{ at centre} = 2 \angle \text{ at circum.}) \\ \therefore D\hat{C}E &\ne C\hat{O}E & \end{array}\] Therefore our assumption is not correct and we can conclude that \(DC\) is not a tangent to the circle passing through the points \(C\), \(F\), \(O\) and \(E\).
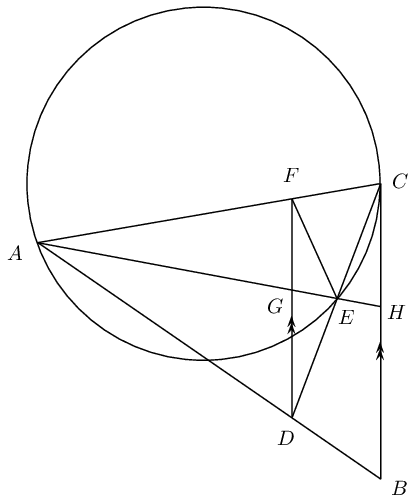
\(FD\) is drawn parallel to the tangent \(CB\)
Prove that:
\(FADE\) is a cyclic quadrilateral
\(F\hat{E}A = \hat{B}\)
|
Previous
8.1 Revision
|
Table of Contents |
Next
8.3 Summary
|