8.3 Summary
|
Previous
8.2 Circle geometry
|
Next
End of chapter exercises
|
8.3 Summary (EMBJC)
- Arc An arc is a portion of the circumference of a circle.
- Chord - a straight line joining the ends of an arc.
- Circumference - perimeter or boundary line of a circle.
- Radius (\(r\)) - any straight line from the centre of the circle to a point on the circumference.
- Diameter - a special chord that passes through the centre of the circle. A diameter is the length of a straight line segment from one point on the circumference to another point on the circumference, that passes through the centre of the circle.
- Segment A segment is a part of the circle that is cut off by a chord. A chord divides a circle into two segments.
- Tangent - a straight line that makes contact with a circle at only one point on the circumference.
-
A tangent line is perpendicular to the radius, drawn at the point of contact with the circle.
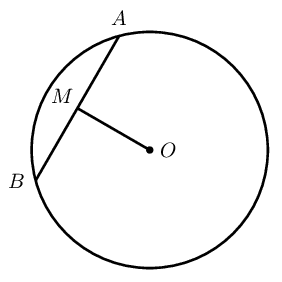 |
|
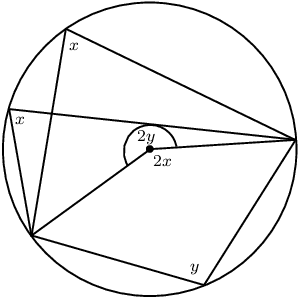 |
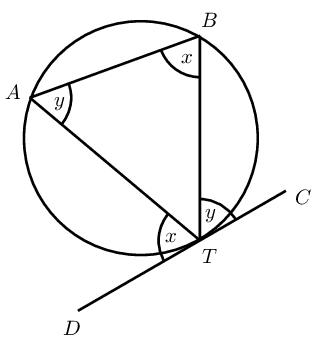
If an arc subtends an angle at the centre of a circle and at the circumference, then the angle at the centre is twice the size of the angle at the circumference. |
 |
Angles at the circumference subtended by the same arc (or arcs of equal length) are equal. |
 |
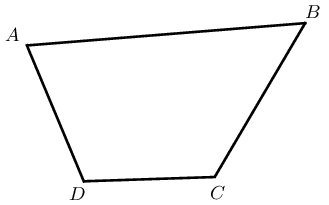
The four sides of a cyclic quadrilateral \(ABCD\) are chords of the circle with centre \(O\).
|
 |
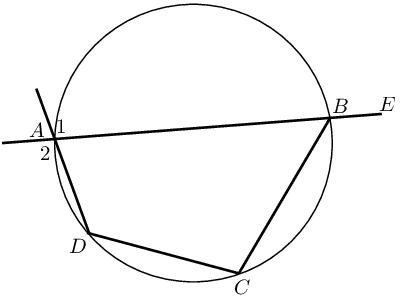
Proving a quadrilateral is cyclic: If \(\hat{A} + \hat{C} = \text{180}\text{°}\) or \(\hat{B} + \hat{D} = \text{180}\text{°}\), then \(ABCD\) is a cyclic quadrilateral. |
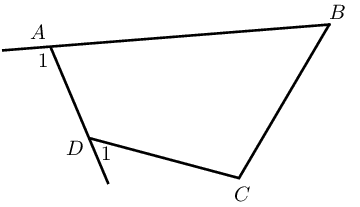 |
If \(\hat{A}_1 = \hat{C}\) or \(\hat{D}_1 = \hat{B}\), then \(ABCD\) is a cyclic quadrilateral. |
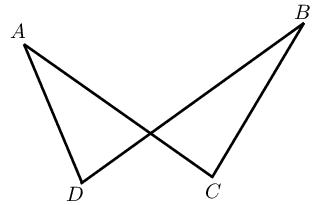 |
If \(\hat{A} = \hat{B}\) or \(\hat{C} = \hat{D}\), then \(ABCD\) is a cyclic quadrilateral. |
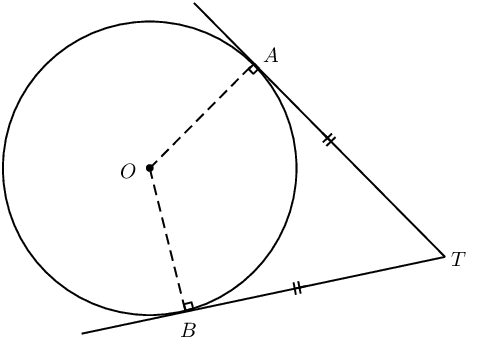 |
If \(AT\) and \(BT\) are tangents to circle \(O\), then
|
 |
|
|
Previous
8.2 Circle geometry
|
Table of Contents |
Next
End of chapter exercises
|
