8.1 Revision
|
Previous
End of chapter exercises
|
Next
8.2 Circle geometry
|
Chapter 8: Euclidean geometry
8.1 Revision (EMBJ6)
Parallelogram (EMBJ7)
- Discuss terminology.
- Converses are not examinable.
- Good practice for answering questions:
- make a neat and accurate drawing
- state triangle/figure being considered
- give statement and appropriate reason
- give a conclusion
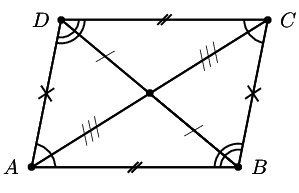
A parallelogram is a quadrilateral with both pairs of opposite sides parallel.
Summary of the properties of a parallelogram:
-
Both pairs of opposite sides are parallel.
-
Both pairs of opposite sides are equal in length.
-
Both pairs of opposite angles are equal.
-
Both diagonals bisect each other.
The mid-point theorem (EMBJ8)
The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the length of the third side.
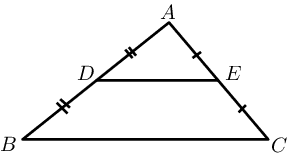
Given: \(AD = DB\) and \(AE = EC\), we can conclude that \(DE \parallel BC\) and \(DE = \frac{1}{2}BC\).
|
Previous
End of chapter exercises
|
Table of Contents |
Next
8.2 Circle geometry
|
