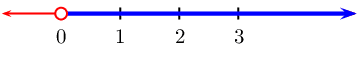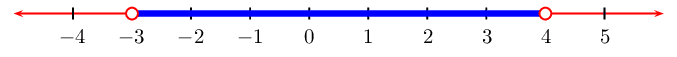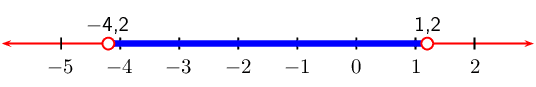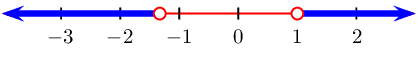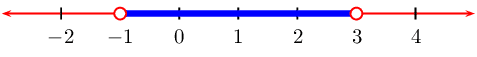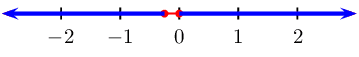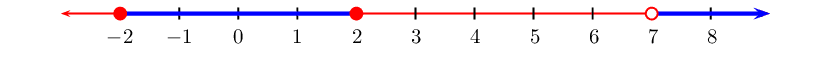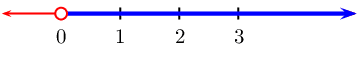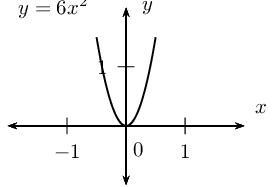\begin{align*}
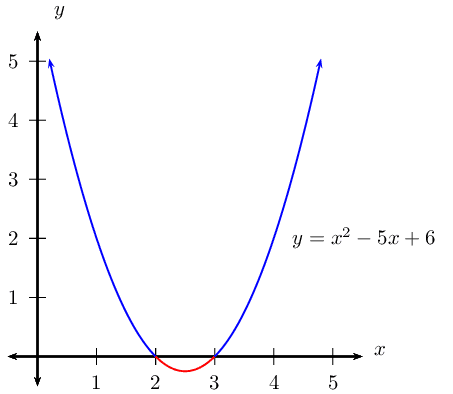
x^{2} - x - 12 & < 0 \\
(x - 4)(x + 3) & < 0
\end{align*}
| Critical values |
|
\(x=-3\) |
|
\(x=4\) |
|
| \(x - 4\) |
\(-\) |
\(-\) |
\(-\) |
\(\text{0}\) |
\(+\) |
| \(x + 3\) |
\(-\) |
\(\text{0}\) |
\(+\) |
\(+\) |
\(+\) |
| \(f(x)= (x - 4)(x + 3)\) |
\(+\) |
\(\text{0}\) |
\(-\) |
\(\text{0}\) |
\(+\) |
From the table we see that \(f(x)\) is less than \(\text{0}\)
when \(-3 < x < 4\)
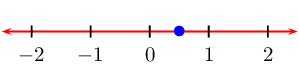
We represent this on a number line:
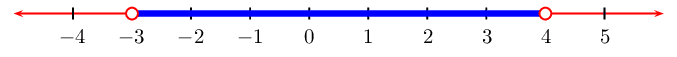
\begin{align*}
3x^{2} + x - 4 & > 0 \\
(3x + 4)(x - 1) & > 0
\end{align*}
| Critical values |
|
\(x=-\frac{4}{3}\) |
|
\(x=1\) |
|
| \(x - 1\) |
\(-\) |
\(-\) |
\(-\) |
\(\text{0}\) |
\(+\) |
| \(3x + 4\) |
\(-\) |
\(\text{0}\) |
\(+\) |
\(+\) |
\(+\) |
| \(f(x)= (3x + 4)(x - 1)\) |
\(+\) |
\(\text{0}\) |
\(-\) |
\(\text{0}\) |
\(+\) |
From the table we see that \(f(x)\) is greater than
\(\text{0}\) when \(x < -\frac{4}{3}\) or when \(x
> 1\)
We represent this on a number line:
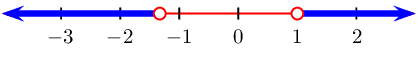
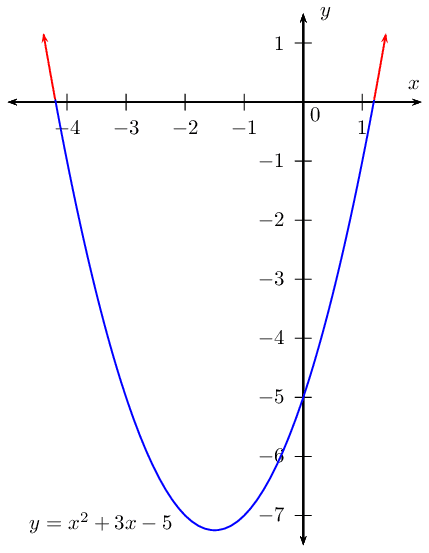
\[y^{2} + y + 2 < 0\]
There are no real solutions.
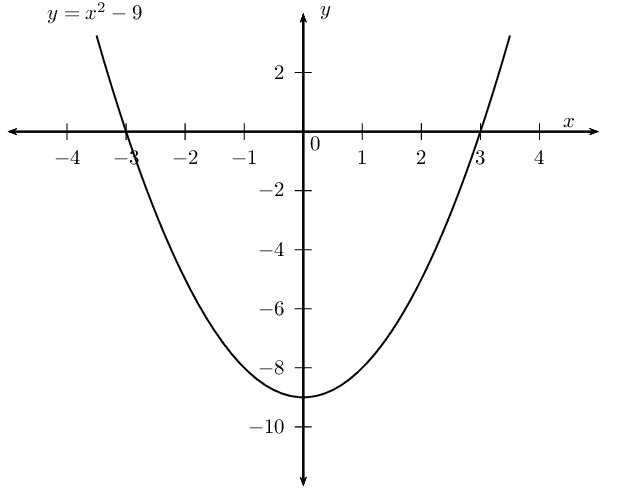
The graph lies above the \(x\)-axis and does not cut the
\(x\)-axis so the function is never negative. There are
no values of \(y\) that will solve this inequality.
\[(3 - t)(1 + t) > 0\]
| Critical values |
|
\(t = -1\) |
|
\(t = 3\) |
|
| \(3 - t\) |
\(+\) |
\(+\) |
\(+\) |
\(\text{0}\) |
\(-\) |
| \(1 + t\) |
\(-\) |
\(\text{0}\) |
\(+\) |
\(+\) |
\(+\) |
| \(f(x)= (3 - t)(1 + t)\) |
\(-\) |
\(\text{0}\) |
\(+\) |
\(\text{0}\) |
\(-\) |
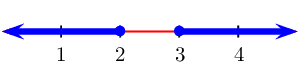
From the table we see that \(f(x)\) is greater than
\(\text{0}\) when \(-1 < t < 3\)
We represent this on a number line:
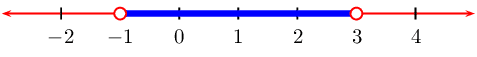
\[s^{2} - 4s + 6 > 0 \\\]
Use the quadratic formula to find critical values:
\begin{align*}
s & = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(6)}}{2(1)} \\
& = \frac{4 \pm \sqrt{16- 24}}{2 } \\
& = \frac{4 \pm \sqrt{-8}}{2}
\end{align*}
Therefore there are no real roots and the graph does not cut
the \(x\)-axis. The graph lies above the \(x\)-axis and
so this inequality is true for all real values of \(s\).
Use the quadratic formula to find critical values:
\begin{align*}
x & = \frac{-(-1) \pm \sqrt{(-1)^2 - 4(7)(8)}}{2(7)} \\
& = \frac{1 \pm \sqrt{1- 224}}{14} \\
& = \frac{1 \pm \sqrt{-223}}{14}
\end{align*}
Therefore there are no real roots and the graph does not cut
the \(x\)-axis. The graph lies above the \(x\)-axis and
so this inequality is true for all real values of \(x\).
\begin{align*}
x & \geq -4x^2 \\
4x^2 + x & \geq 0 \\
x(4x + 1) & \geq 0
\end{align*}
| Critical values |
|
\(x = -\frac{1}{4}\) |
|
\(x = 0\) |
|
| \(x\) |
\(-\) |
\(-\) |
\(-\) |
\(\text{0}\) |
\(+\) |
| \(4x + 1\) |
\(-\) |
\(\text{0}\) |
\(+\) |
\(+\) |
\(+\) |
| \(f(x)= x(4x + 1)\) |
\(+\) |
\(\text{0}\) |
\(-\) |
\(\text{0}\) |
\(+\) |
From the table we see that \(f(x)\) is greater than
\(\text{0}\) when \(x \leq -\frac{1}{4}\) or \(x \geq
0\).
We can represent this on a number line:
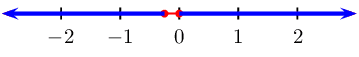
\[2x^{2} + x + 6 \le 0\]
There are no real roots and the graph does not cut the
\(x\)-axis. The graph lies above the \(x\)-axis and so
this inequality is never true.
\(\dfrac{x}{x-3}<2\), \(x\ne 3\)
We first solve the equation:
\begin{align*}
\dfrac{x}{x-3} & < 2 \\
\dfrac{x}{x-3} - 2 & < 0 \\
\dfrac{x - 2(x-3)}{x-3}& < 0 \\
\dfrac{x - 2x + 6}{x-3}& < 0 \\
\dfrac{-x + 6}{x-3}& < 0 \\
\dfrac{-(x - 6)}{x-3}& < 0 \\
\dfrac{x - 6}{x-3}& > 0 \\
x & = 6
\end{align*}
| Critical values |
|
\(x = 3\) |
|
\(x = 6\) |
|
| \(x - 3\) |
\(-\) |
undef |
\(+\) |
\(+\) |
\(+\) |
| \(x - 6\) |
\(-\) |
\(-\) |
\(-\) |
\(\text{0}\) |
\(+\) |
| \(f(x)= x - 6\) |
\(+\) |
undef |
\(-\) |
\(\text{0}\) |
\(+\) |
From the table we see that \(f(x) > 0\) when \(x < 3
\text{ or } x > 6\) with \(x \ne 3\).
We can represent this on a number line:

\(\dfrac{x^2 + 4}{x - 7} \geq 0\), \(x \ne 7\)
We first simplify the fraction:
\[\dfrac{(x + 2)(x - 2)}{x - 7} \geq 0\]
| Critical values |
|
\(x = -2\) |
|
\(x = 2\) |
|
\(x = 7\) |
|
| \(x + 2\) |
\(-\) |
\(\text{0}\) |
\(+\) |
\(+\) |
\(+\) |
\(+\) |
\(+\) |
| \(x - 2\) |
\(-\) |
\(-\) |
\(-\) |
\(\text{0}\) |
\(+\) |
\(+\) |
\(+\) |
| \(x - 7\) |
\(-\) |
\(-\) |
\(-\) |
\(-\) |
\(-\) |
undef |
\(+\) |
| \(f(x)= \dfrac{(x + 2)(x - 2)}{x - 7}\) |
\(-\) |
\(\text{0}\) |
\(+\) |
\(\text{0}\) |
\(-\) |
undef |
\(+\) |
From the table we see that \(f(x)\) is greater than
\(\text{0}\) when \(-2 \leq x \leq 2\) and \(x > 7\)
with \(x \ne 7\).
We can represent this on a number line:
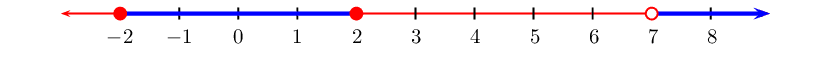
\(\dfrac{x + 2}{x} - 1 \geq 0\), \(x \ne 0\)
We first simplify the equation:
\begin{align*}
\frac{x + 2}{x} - 1 & \ge 0 \\
\frac{x + 2 - x}{x}& \ge 0 \\
\frac{2}{x} & \ge 0 \\
\text{Therefore } x & > 0
\end{align*}
The solution is \(x > 0\) with \(x \ne 0\).
We can represent this on a number line: