2.6 Nature of roots | Equations and inequalities

2.6 Nature of roots (EMBFP)

Investigating the nature of roots

Use the quadratic formula to determine the roots of the quadratic equations given below and take special note of:
- the expression under the square root sign and
- the type of number for the final answer (rational/irrational/real/imaginary)
1. \(x^2 - 6x + 9 = 0\)
2. \(x^2 - 4x + 3 = 0\)
3. \(x^2 - 4x - 3 = 0\)
4. \(x^2 - 4x + 7 = 0\)

Choose the appropriate words from the table to describe the roots obtained for the equations above.

rational	unequal	real
imaginary	not perfect square	equal
perfect square	irrational	undefined

The expression under the square root, \(b^2 - 4ac\), is called the discriminant. Can you make a conjecture about the relationship between the discriminant and the roots of quadratic equations?

The discriminant (EMBFQ)

The discriminant is defined as \(\Delta ={b}^{2}-4ac\).

This is the expression under the square root in the quadratic formula. The discriminant determines the nature of the roots of a quadratic equation. The word ‘nature’ refers to the types of numbers the roots can be — namely real, rational, irrational or imaginary. \(Δ\) is the Greek symbol for the letter D.

For a quadratic function \(f\left(x\right)=a{x}^{2}+bx+c\), the solutions to the equation \(f\left(x\right)=0\) are given by the formula

\(x=\dfrac{-b±\sqrt{{b}^{2}-4ac}}{2a}=\dfrac{-b±\sqrt{\Delta }}{2a}\)

If \(Δ < 0\), then roots are imaginary (non-real) and beyond the scope of this book.
If \(Δ \geq 0\), the expression under the square root is non-negative and therefore roots are real. For real roots, we have the following further possibilities.
If \(Δ = 0\), the roots are equal and we can say that there is only one root.
If \(Δ > 0\), the roots are unequal and there are two further possibilities.
\(Δ\) is the square of a rational number: the roots are rational.
\(Δ\) is not the square of a rational number: the roots are irrational and can be expressed in decimal or surd form.

Nature of roots	Discriminant	\(a>0\)	\(a<0\)
Roots are non-real	\(\Delta <0\)
Roots are real and equal	\(\Delta=0\)
Roots are real and unequal: rational roots irrational roots	\(Δ > 0\) \(Δ =\) squared rational \(Δ =\) not squared rational

Worked example 13: Nature of roots

Show that the roots of \(x^2-2x-7=0\) are irrational.

Interpret the question

For roots to be real and irrational, we need to calculate \(Δ\) and show that it is greater than zero and not a perfect square.

Check that the equation is in standard form \(ax^2+bx+c=0\)

\[x^2-2x-7=0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 1; \qquad b = -2; \qquad c = -7\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (-2)^2-4(1)(-7) \\ &= 4+28 \\ &= 32 \end{align*}

We know that \(32 > 0\) and is not a perfect square.

The graph below shows the roots of the equation \(x^2 - 2x - 7 = 0\). Note that the graph does not form part of the answer and is included for illustration purposes only.

Write the final answer

We have calculated that \(Δ > 0\) and is not a perfect square, therefore we can conclude that the roots are real, unequal and irrational.

temp text

Worked example 14: Nature of roots

For which value(s) of \(k\) will the roots of \(6x^2 + 6 = 4kx\) be real and equal?

Interpret the question

For roots to be real and equal, we need to solve for the value(s) of \(k\) such that \(\Delta =0\).

Check that the equation is in standard form \(ax^2+bx+c=0\)

\[6x^2-4kx+6=0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 6; \qquad b = -4k; \qquad c = 6\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (-4k)^2-4(6)(6) \\ &= 16k^2-144 \end{align*}

For roots to be real and equal, \(\Delta =0\).

\begin{align*} Δ &= 0 \\ 16k^2 - 144 &= 0 \\ 16(k^2-9)&= 0 \\ (k-3)(k+3)&= 0 \end{align*}

Therefore \(k = 3\) or \(k = -3\).

Check both answers by substituting back into the original equation

For \(k = 3\): \begin{align*} 6x^2-4(3)x + 6 &= 0 \\ 6x^2-12x + 6 &= 0 \\ x^2-2x + 1 &= 0 \\ (x-1)(x-1)&= 0 \\ (x-1)^2&= 0 \\ \text{Therefore } x &= 1 \end{align*}

We see that for \(k = 3\) the quadratic equation has real, equal roots \(x = 1\).

For \(k = - 3\): \begin{align*} 6x^2-4(-3)x + 6 &= 0 \\ 6x^2+12x + 6 &= 0 \\ x^2+2x + 1 &= 0 \\ (x+1)(x+1)&= 0 \\ (x+1)^2&= 0 \\ \text{Therefore } x &= -1 \end{align*}

We see that for \(k = -3\) the quadratic equation has real, equal roots \(x = -1\).

Write the final answer

For the roots of the quadratic equation to be real and equal, \(k = 3\) or \(k = -3\). \(\)

temp text

Worked example 15: Nature of roots

Show that the roots of \((x+h)(x+k)=4d^2\) are real for all real values of \(h, k\) and \(d\).

Interpret the question

For roots to be real, we need to calculate \(Δ\) and show that \(Δ \ge 0\) for all real values of \(h\), \(k\) and \(d\).

Check that the equation is in standard form \(ax^2+bx+c=0\)

Expand the brackets and gather like terms

\begin{align*} (x+h)(x+k) &= 4d^2 \\ x^2 + hx +kx +hk -4d^2 &= 0 \\ x^2 + (h+k)x + (hk -4d^2) &= 0 \end{align*}

Identify the coefficients to substitute into the formula for the discriminant

\[a = 1; \qquad b = h+k; \qquad c = hk-4d^2\]

Write down the formula and substitute values

\begin{align*} \Delta &= b^2-4ac \\ &= (h+k)^2-4(1)(hk-4d^2) \\ &= h^2+2hk+k^2-4hk+16d^2 \\ &= h^2-2hk+k^2+16d^2 \\ &= (h - k)^2+(4d)^2 \end{align*}

For roots to be real, \(\Delta \geq 0\).

\begin{align*} \text{We know that } (4d)^2 &\geq 0 \\ \text{and } (h - k)^2 &\geq 0 \\ \text{so then } (h - k)^2+ (4d)^2 &\geq 0 \\ \text{therefore } \Delta &\geq 0 \end{align*}

Write the final answer

We have shown that \(\Delta \geq 0\), therefore the roots are real for all real values of \(h, k\) and \(d\).

temp text

From past papers

Textbook Exercise 2.7

\(x^2 + 3x = -2\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[x^2 + 3x + 2 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 1; \qquad b = 3; \qquad c = 2\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (3)^2 - 4(1)(2) \\ &= 9 - 8 \\ &= 1 \end{align*}

We know that \(1 > 0\) and is a perfect square.

We have calculated that \(Δ > 0\) and is a perfect square, therefore we can conclude that the roots are real, unequal and rational.

\(x^2 + 9 = 6x\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[x^2 - 6x + 9 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 1; \qquad b = -6; \qquad c = 9\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (-6)^2 - 4(1)(9) \\ &= 36 - 36 \\ &= 0 \end{align*}

We have calculated that \(Δ = 0\) therefore we can conclude that the roots are real and equal.

\(6y^2 - 6y - 1 = 0\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[6y^2 - 6y - 1 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 6; \qquad b = -6; \qquad c = -1\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (-6)^2 - 4(6)(-1) \\ &= 36 + 36 \\ &= 72 \end{align*}

We know that \(72 > 0\) and is not a perfect square.

We have calculated that \(Δ > 0\) and is not a perfect square, therefore we can conclude that the roots are real, unequal and irrational.

\(4t^2 - 19t - 5 = 0\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[4t^2 - 19t - 5 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 4; \qquad b = -19; \qquad c = -5\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (-19)^2 - 4(4)(-5) \\ &= 361 + 80 \\ &= 441 \end{align*}

We know that \(441 > 0\) and is a perfect square.

We have calculated that \(Δ > 0\) and is a perfect square, therefore we can conclude that the roots are real, unequal and rational.

\(z^2 = 3\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[z^2 - 3 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 1; \qquad b = 0; \qquad c = -3\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (0)^2 - 4(1)(-3) \\ &= 0 + 12 \\ &= 12 \end{align*}

We know that \(12 > 0\) and is not a perfect square.

We have calculated that \(Δ > 0\) and is not a perfect square, therefore we can conclude that the roots are real, unequal and irrational.

\(0 = p^2 + 5p + 8\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[p^2 + 5p + 8 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 1; \qquad b = 5; \qquad c = 8\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (5)^2 - 4(1)(8) \\ &= 25 - 32 \\ &= -7 \end{align*}

We know that \(-7 < 0\).

We have calculated that \(Δ < 0\), therefore we can conclude that the roots are non-real.

\(x^2 = 36\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[x^2 - 36 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 1; \qquad b = 0; \qquad c = -36\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (0)^2 - 4(1)(-36) \\ &= 0 + 144 \\ &= 144 \end{align*}

We know that \(144 > 0\) and is a perfect square.

We have calculated that \(Δ > 0\) and is a perfect square, therefore we can conclude that the roots are real, unequal and rational.

\(4m + m^2 = 1\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[m^2 + 4m - 1 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 1; \qquad b = 4; \qquad c = -1\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (4)^2 - 4(1)(-1) \\ &= 16 + 4 \\ &= 20 \end{align*}

We know that \(20 > 0\) and is not a perfect square.

We have calculated that \(Δ > 0\) and is not a perfect square, therefore we can conclude that the roots are real, unequal and irrational.

\(11 - 3x + x^2 = 0\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[x^2 - 3x + 11 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 1; \qquad b = -3; \qquad c = 11\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (-3)^2 - 4(1)(11) \\ &= 9 - 44 \\ &= -35 \end{align*}

We know that \(-35 < 0\).

We have calculated that \(Δ < 0\), therefore we can conclude that the roots are non-real.

\(y^2 + \dfrac{1}{4} = y\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[4y^2 - 4y + 1 = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = 4; \qquad b = -4; \qquad c = 1\]

Write down the formula and substitute values.

\begin{align*} Δ &= b^2-4ac \\ &= (-4)^2 - 4(4)(1) \\ &= 16 - 16 \\ &= 0 \end{align*}

We have calculated that \(Δ = 0\), therefore we can conclude that the roots are real and equal.

Show that the discriminant is given by: \(\Delta ={k}^{2}+6bk+{b}^{2}+8\)

We write the equation in standard form \(ax^2+bx+c=0\):

\[(k + 1)x^2 + (b + 3k)x - 2 + 2k = 0\]

Identify the coefficients to substitute into the formula for the discriminant

\[a = k + 1; \qquad b = b + 3k; \qquad c = -2 + 2k\]

Write down the formula and substitute values

\begin{align*} Δ &= b^2-4ac \\ &= (b + 3k)^2 - 4(k + 1)(2k - 2) \\ &= b^{2} + 6bk + 9k^{2} -4(2k^{2} - 2) \\ &= b^{2} + 6bk + 9k^{2} -8k^{2} + 8 \\ &= k^{2} + 6bk + b^{2} + 8 \end{align*}

If \(b=0\), discuss the nature of the roots of the equation.

When \(b=0\) the discriminant is:

\[Δ = k^{2} + 8\]

This is positive for all values of \(k\) and greater than \(\text{0}\) for all values of \(k\).

For example if \(k = 0\) then \(Δ = 8\), if \(k = -1\) then \(Δ = 9\) and if \(k = 1\) then \(Δ = 9\).

So the roots are real and unequal. We cannot say if the roots are rational or irrational since this depends on the exact value of \(k\).

If \(b=2\), find the value(s) of \(k\) for which the roots are equal.

When \(b=2\) the discriminant is:

\begin{align*} Δ & = k^{2} + 6(2)k + (2)^{2} + 8 \\ & = k^{2} + 12k + 12 \end{align*}

We set this equal to \(\text{0}\) since we want to find the values of \(k\) that will make the roots equal.

\begin{align*} 0 & = k^{2} + 12k + 12 \\ k & = \dfrac{-12 \pm \sqrt{(12)^{2} - 4(1)(12)}}{2(1)} \\ & = \dfrac{-12 \pm \sqrt{144 - 48}}{2} \\ & = \dfrac{-12 \pm \sqrt{96}}{2} \\ & = \dfrac{-12 \pm 4\sqrt{6}}{2} \\ k = -6 + 2\sqrt{6} & \text{ or } k = -6 - 2\sqrt{6} \end{align*}

The roots will be equal if \(k = -6 \pm 2\sqrt{6}\).

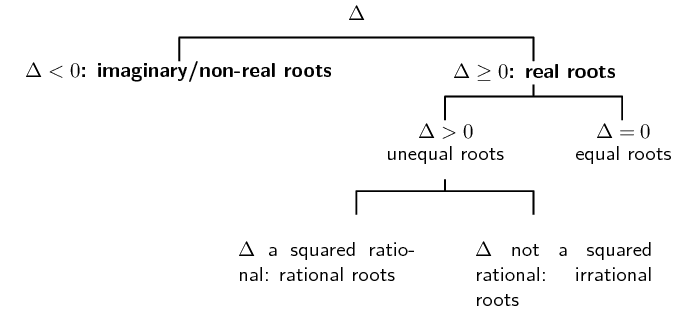
Show that \({k}^{2}{x}^{2}+2=kx-{x}^{2}\) has non-real roots for all real values for \(k\).

[IEB, Nov. 2002, HG]

\begin{align*} k^2 x^2 + x^2 - kx +2 &= 0\\ a &= (k^2+1)\\ b&= -k\\ c&=2\\ \Delta &= b^2-4ac\\ &= (-k)^2 - 4(k^2+1)(2)\\ &=k^2-8k^2-8\\ &=-7k^2 - 8\\ &=-(7k^2 + 8)\\ \Delta & < 0 \end{align*}Therefore the roots are non-real.

Find the greatest value of value \(k\) such that \(k \in \mathbb{Z}\).

\begin{align*} x^2 +12x &= 3kx^2 +2\\ 3kx^2 -x^2 - 12x+2&=0\\ x^2(3k-1)-12x+2&=0\\ a&=3k-1\\ b&=-12\\ c&=2\\ \text{Given } \Delta &\geq 0\\ \therefore b^2-4ac &\geq 0\\ \therefore (-12)^2 - 4(3k-1)(2) &\geq 0\\ 144 -24k + 8 &\geq 0 \\ 152 - 24k &\geq 0 \\ 152 &\geq 24k \\ \frac{19}{3} &\geq k \\ \therefore k &\leq \frac{19}{3} \\ \therefore k &\leq 6\frac{1}{3} \end{align*}

Since \(k\) needs to be an integer, the greatest value of \(k\) is \(\text{6}\).

Find one rational value of \(k\) for which the above equation has rational roots.

For rational roots we need \(\Delta\) to be a perfect square.

\begin{align*} \Delta &= b^2-4ac \\ &=152-24k\\ \text{if } k&=\frac{1}{3}\\ \Delta &= 152 - 24\left(\frac{1}{3}\right)\\ &=152-8\\ &=144\\ &=12^2 \end{align*}

This is a perfect square. Therefore if \(k=\frac{1}{3}\), the roots will be rational.

Find a value of \(k\) for which the roots are equal.

We first need to write the equation in standard form:

\begin{align*} k(2x - 5) & = x^2-4 \\ 2kx - 5k & = x^2-4 \\ 0 & = x^{2} - 4 - 2kx + 5k \\ 0 & = x^{2} - 2kx + 5k - 4 \end{align*}

Next we note that \(a = 1; \qquad b = -2k; \qquad c = 5k - 4\).

Now we can find the discriminant:

\begin{align*} Δ &= b^2-4ac \\ &= (-2k)^2 - 4(1)(5k - 4) \\ &= 4k^{2} - 20k + 16 \end{align*}

To find the values of \(k\) that make the roots equal, we set this equal to \(\text{0}\) and solve for \(k\):

\begin{align*} 0 &= 4k^{2} - 20k + 16 \\ &= k^{2} - 5k + 4 \\ &= (k - 4)(k - 1) \\ k = 4 & \text{ or } k = 1 \end{align*}

Find an integer \(k\) for which the roots of the equation will be rational and unequal.

The discriminant is:

\[\Delta = 4k^{2} - 20k + 16\]

To find a value of \(k\) that makes the roots rational and unequal the discriminant must be greater than \(\text{0}\) and a perfect square.

We try setting the discriminant equal to \(\text{1}\):

\begin{align*} \Delta & = 4k^{2} - 20k + 16 \\ 1 & = 4k^{2} - 20k + 16 \\ 0 & = 4k^{2} - 20k + 15 \end{align*}

This does not give an integer value of \(k\) so we try \(\text{4}\):

\begin{align*} 4 & = 4k^{2} - 20k + 16 \\ 0 & = 4k^{2} - 20k + 12 \\ & = k^{2} - 5k + 3 \end{align*}

This does not give an integer value of \(k\) so we try \(\text{9}\):

\begin{align*} 9 & = 4k^{2} - 20k + 16 \\ 0 & = 4k^{2} - 20k + 5 \end{align*}

This does not give an integer value of \(k\) so we try \(\text{16}\):

\begin{align*} 16 & = 4k^{2} - 20k + 16 \\ 0 & = 4k^{2} - 20k \\ & = k^{2} - 5k \\ k = 0 & \text{ or } k = 5 \end{align*}

So if \(k=0\) or \(k=5\) the roots will be rational and unequal.

Prove that the roots of the equation \({x}^{2}-\left(a+b\right)x+ab-{p}^{2}=0\) are real for all real values of \(a\), \(b\) and \(p\).

We need to prove that \(\Delta \geq 0\).

\begin{align*} \Delta &=(-a-b)^2 - 4(ab-p^2)\\ &=a^2 + 2ab + b^2 - 4ab + 4p^2\\ &=a^2 - 2ab + b^2 + 4p^2\\ &=(a-b)^2 + 4p^2 \end{align*}

\(\Delta \geq 0\) for all real values of \(a\), \(b\) and \(p\). Therefore the roots are real for all real values of \(a\), \(b\) and \(p\).

When will the roots of the equation be equal?

The roots are equal when \(\Delta = 0\), that is when \(a=b\) and \(p=0\).

If \(b\) and \(c\) can take on only the values \(\text{1}\), \(\text{2}\) or \(\text{3}\), determine all pairs (\(b; c\)) such that \({x}^{2}+bx+c=0\) has real roots.

[IEB, Nov. 2005, HG]

We need to find the values of \(a\), \(b\) and \(c\) for which \(\Delta \geq 0\).

\begin{align*} a&=1\\ b&=\text{1,2} \text{ or }3\\ c&=\text{1,2} \text{ or }3\\ \\ \Delta &= b^2-4ac\\ &= b^2 - 4(1)c \end{align*}

Possible pair values of \((b;c)\): \((1;1),~(1;2),~(1;3),~(2;1),~(2;2),~(2;3),~(3;1),~(3;2),~(3;3)\). Corresponding values of \(\Delta\): \((\Delta < 0),~(\Delta < 0),~(\Delta < 0),~(\Delta = 0),~(\Delta < 0),~(\Delta < 0),~(\Delta >0),~(\Delta > 0),~(\Delta < 0)\)

\(\Delta ≥ 0\) (and therefore the roots are real) for \((b;c) = (2;1),~(3;1),~(3;2)\)

2.5 Finding the equation

Table of Contents

2.7 Quadratic inequalities