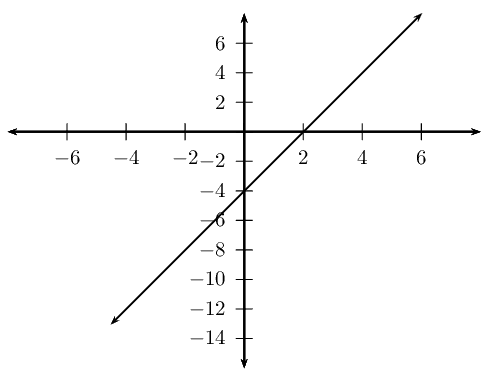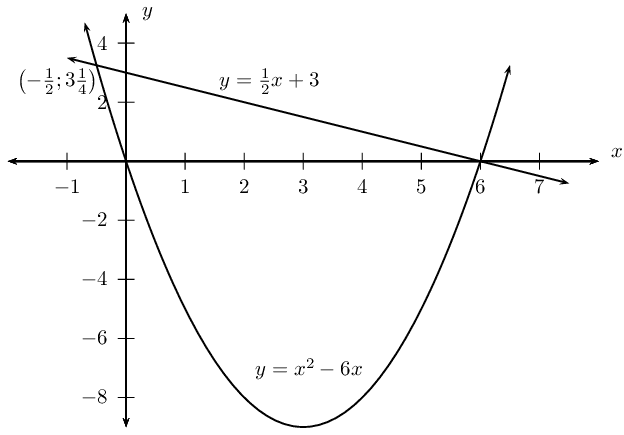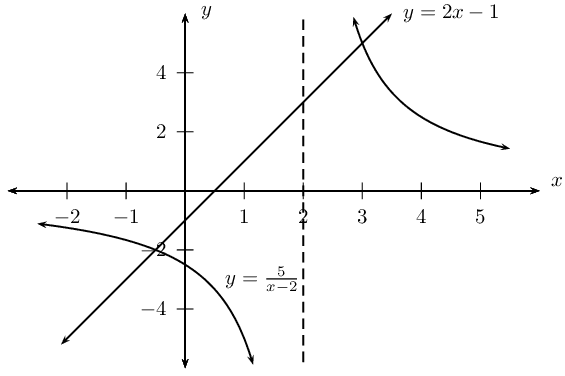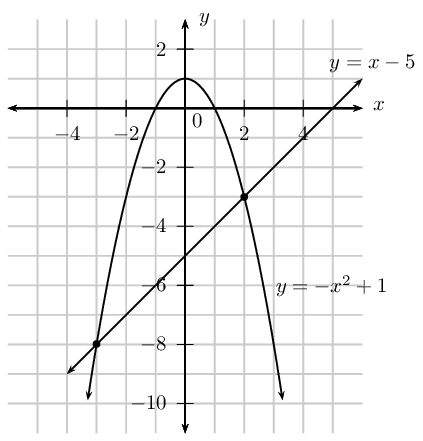\({x}^{2}-1-y=0\)
\(y+x-5=0\)
Make \(y\) the subject of both equations
For the first equation we have:
\begin{align*}
x^{2} - 1 - y &= 0 \\
y &= x^2 - 1
\end{align*}
and for the second equation:
\begin{align*}
y + x - 5 &= 0 \\
y &= -x + 5
\end{align*}
Draw the straight line graph and parabola on the same system of axes:
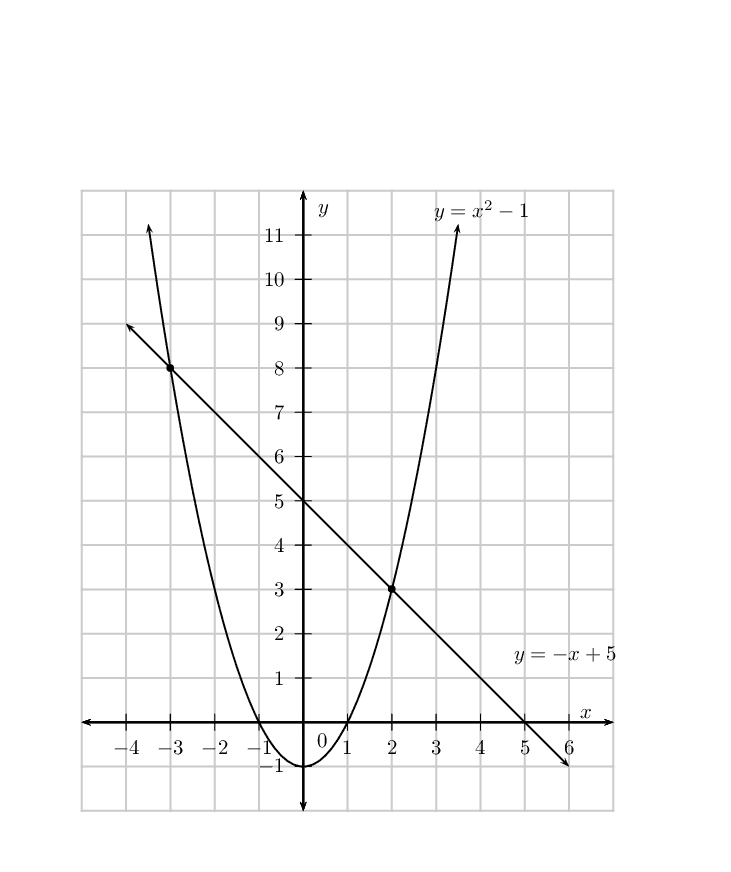
From the diagram we see that the graphs intersect at \((-3;8)\) and \((2;3)\).
We can solve algebraically to check. Doing this we find the same solution.
The solutions to the system of simultaneous equations are \((-3;8)\) and \((2;3)\).
\(x+y-10=0\)
\({x}^{2}-2-y=0\)
Make \(y\) the subject of both equations
For the first equation we have:
\begin{align*}
x + y - 10 &= 0 \\
y &= -x + 10
\end{align*}
and for the second equation:
\begin{align*}
x^{2} - 2 - y &= 0 \\
y &= x^{2} - 2
\end{align*}
Draw the straight line graph and parabola on the same system of axes:
From the diagram we see that the graphs intersect at \((-4;14)\) and \((3;7)\).
We can solve algebraically to check. Doing this we find the same solution.
The solutions to the system of simultaneous equations are \((-4;14)\) and \((3;7)\).
Make \(y\) the subject of both equations
For the first equation we have:
\begin{align*}
xy &= 12 \\
y &= \frac{12}{x}
\end{align*}
and for the second equation:
\begin{align*}
7 &= x + y \\
y &= 7 - x
\end{align*}
Draw the two graphs on the same system of axes:
We also note that this sytem of equations has the followig restrictions: \(x \ne 0\) and \(y \ne 0\)
From the diagram we see that the graphs intersect at \((3;4)\) and \((4;3)\).
We can solve algebraically to check. Doing this we find the same solution.
The solutions to the system of simultaneous equations are \((3;4)\) and \((4;3)\).
\(6-4x-y=0\)
\(12-2{x}^{2}-y=0\)
Make \(y\) the subject of both equations
For the first equation we have:
\begin{align*}
6 - 4x - y &= 0 \\
y &= -4x + 6
\end{align*}
and for the second equation:
\begin{align*}
12 - 2x^{2} - y &= 0 \\
y &= -2x^{2} + 12
\end{align*}
Draw the two graphs on the same system of axes:
From the diagram we see that the graphs intersect at approximately \((4;-10)\) and \((-2;14)\).
We can solve algebraically to check (and to get a more accurate answer). Doing this gives:
\begin{align*}
-4x + 6 &= -2x^{2} + 12 \\
2x - 3 &= x^{2} - 6 \\
x^{2} - 2x - 9 & = 0 \\
x & = \dfrac{-(-2) \pm \sqrt{(-2)^{2} - 4(1)(-9)}}{2(1)} \\
x & = \dfrac{2 \pm \sqrt{(4 + 36}}{2} \\
x & = \dfrac{2 \pm \sqrt{40}}{2}
\end{align*}
Solving for \(y\) gives:
\begin{align*}
y & = -4\left(\dfrac{2 \pm \sqrt{40}}{2} \right) + 6 \\
&= -2(2 \pm \sqrt{40}) + 6 \\
& = -4 \pm 2\sqrt{40} + 6 \\
& = 2 \pm 2\sqrt{40}
\end{align*}