4.3 Inclination of a line | Analytical geometry

4.3 Inclination of a line (EMBGD)

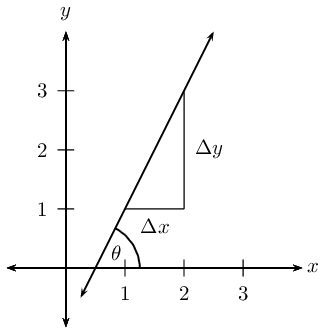
The diagram shows that a straight line makes an angle \(\theta\) with the positive \(x\)-axis. This is called the angle of inclination of a straight line.

We notice that if the gradient changes, then the value of \(\theta\) also changes, therefore the angle of inclination of a line is related to its gradient. We know that gradient is the ratio of a change in the \(y\)-direction to a change in the \(x\)-direction:

\[m=\frac{\Delta y}{\Delta x}\]

From trigonometry we know that the tangent function is defined as the ratio:

\[\tan \theta = \frac{\text{opposite side}}{\text{adjacent side}}\]

And from the diagram we see that

\begin{align*} \tan \theta &= \dfrac{\Delta y}{\Delta x} \\ \therefore m &= \tan \theta \qquad \text{ for } \text{0}\text{°} \leq \theta < \text{180}\text{°} \end{align*}

Therefore the gradient of a straight line is equal to the tangent of the angle formed between the line and the positive direction of the \(x\)-axis.

Vertical lines

\(\theta = \text{90}\text{°}\)
Gradient is undefined since there is no change in the \(x\)-values (\(\Delta x = 0\)).
Therefore \(\tan \theta\) is also undefined (the graph of \(\tan \theta\) has an asymptote at \(\theta = \text{90}\text{°}\)).

Horizontal lines

\(\theta = \text{0}\text{°}\)
Gradient is equal to \(\text{0}\) since there is no change in the \(y\)-values (\(\Delta y = 0\)).
Therefore \(\tan \theta\) is also equal to \(\text{0}\) (the graph of \(\tan \theta\) passes through the origin \((\text{0}\text{°};0))\).

Lines with negative gradients

If a straight line has a negative gradient (\(m < 0\), \(\tan \theta < 0\)), then the angle formed between the line and the positive direction of the \(x\)-axis is obtuse.

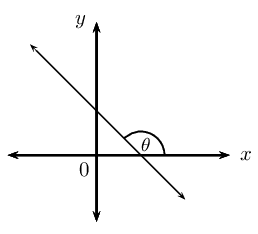
From the CAST diagram in trigonometry, we know that the tangent function is negative in the second and fourth quadrant. If we are calculating the angle of inclination for a line with a negative gradient, we must add \(\text{180}\text{°}\) to change the negative angle in the fourth quadrant to an obtuse angle in the second quadrant:

If we are given a straight line with gradient \(m = -\text{0,7}\), then we can determine the angle of inclination using a calculator:

\begin{align*} \tan \theta &= m \\ &= -\text{0,7} \\ \therefore \theta &= \tan^{-1}(-\text{0,7}) \\ &= -\text{35,0}\text{°} \end{align*}

This negative angle lies in the fourth quadrant. We must add \(\text{180}\)\(\text{°}\) to get an obtuse angle in the second quadrant:

\begin{align*} \theta &= -\text{35,0}\text{°} + \text{180}\text{°} \\ &= \text{145}\text{°} \end{align*}

And we can always use our calculator to check that the obtuse angle \(\theta = \text{145}\text{°}\) gives a gradient of \(m = -\text{0,7}\).

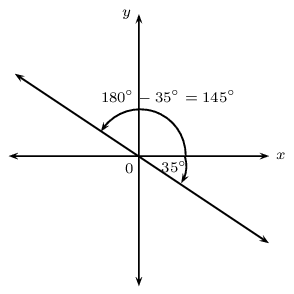
Angle of inclination

Textbook Exercise 4.5

\(\text{60}\text{°}\)

\begin{align*} m &= \tan \theta \\ &= \tan \text{60}\text{°} \\ \therefore m &= \text{1,7} \end{align*}

\(\text{135}\text{°}\)

\begin{align*} m &= \tan \theta \\ &= \tan \text{135}\text{°} \\ \therefore m &= -\text{1} \end{align*}

\(\text{0}\text{°}\)

\begin{align*} m &= \tan \theta \\ &= \tan \text{0}\text{°} \\ \therefore m &= \text{0} \end{align*}

\(\text{54}\text{°}\)

\begin{align*} m &= \tan \theta \\ &= \tan \text{54}\text{°} \\ \therefore m &= \text{1,4} \end{align*}

\(\text{90}\text{°}\)

\begin{align*} m &= \tan \theta \\ &= \tan \text{90}\text{°} \\ \therefore m & \text{ is undefined} \end{align*}

\(\text{45}\text{°}\)

\begin{align*} m &= \tan \theta \\ &= \tan \text{45}\text{°} \\ \therefore m &= \text{1} \end{align*}

\(\text{140}\text{°}\)

\begin{align*} m &= \tan \theta \\ &= \tan \text{140}\text{°} \\ \therefore m &= -\text{0,8} \end{align*}

\(\text{180}\text{°}\)

\begin{align*} m &= \tan \theta \\ &= \tan \text{180}\text{°} \\ \therefore m &= \text{0} \end{align*}

\(\text{75}\text{°}\)

\begin{align*} m &= \tan \theta \\ &= \tan \text{75}\text{°} \\ \therefore m &= \text{3,7} \end{align*}

a line with \(m = \dfrac{3}{4}\)

\begin{align*} \tan \theta &= m \\ &= \frac{3}{4} \\ \theta &= \tan^{-1} \left( \text{0,75} \right) \\ \therefore \theta &= \text{36,8}\text{°} \end{align*}

\(2y - x = 6\)

\begin{align*} 2y - x &= 6 \\ 2y &= x + 6 \\ y &= \frac{1}{2}x + 3 \\ \tan \theta &= m \\ &= \frac{1}{2} \\ \theta &= \tan^{-1} \left( \text{0,5} \right) \\ \therefore \theta &= \text{26,6}\text{°} \end{align*}

the line passes through the points \((-4;-1)\) and \((2;5)\)

\begin{align*} m &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{5 + 1}{2 + 4} \\ &= \frac{6}{6} \\ \therefore m &= 1 \\ \tan \theta &= 1 \\ \theta &= \tan^{-1} \left( \text{1} \right) \\ \therefore \theta &= \text{45}\text{°} \end{align*}

\(y=4\)

Horizontal line

\(x = 3y + \frac{1}{2}\)

\begin{align*} x &= 3y + \frac{1}{2} \\ x - \frac{1}{2} &= 3y \\ \frac{1}{3}x - \frac{1}{6} &= y \\ \therefore m &= \frac{1}{3} \\ \theta &= \tan^{-1} \left( \frac{1}{3} \right) \\ \therefore \theta &= \text{18,4}\text{°} \end{align*}

\(x=-\text{0,25}\)

Vertical line

the line passes through the points \((2;5)\) and \((\frac{2}{3};1)\)

\begin{align*} m &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{1 - 5}{\frac{2}{3} -2} \\ &= \frac{-4}{-\frac{4}{3}} \\ \therefore m &= 3 \\ \theta &= \tan^{-1} \left( \text{3} \right) \\ \therefore \theta &= \text{71,6}\text{°} \end{align*}

a line with gradient equal to \(\text{0,577}\)

\begin{align*} m &= \text{0,577} \\ \theta &= \tan^{-1} \left( \text{0,577} \right) \\ \therefore \theta &= \text{30}\text{°} \end{align*}

Worked example 8: Inclination of a straight line

Determine the angle of inclination (correct to \(\text{1}\) decimal place) of the straight line passing through the points \((2;1)\) and \((-3;-9)\).

Draw a sketch

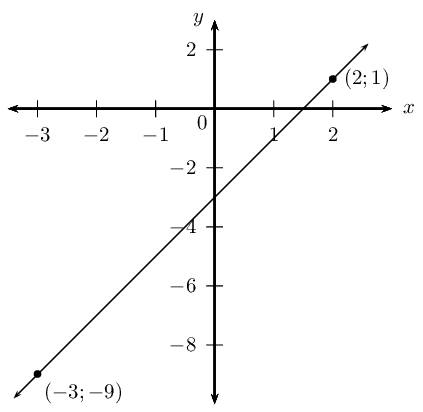
Assign variables to the coordinates of the given points

\[x_1 = 2; \qquad y_1 = 1; \qquad x_2 = -3; \qquad y_2 = -9\]

Determine the gradient of the line

\begin{align*} m &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{-9-1}{-3-2} \\ &= \frac{-10}{-5} \\ \therefore m &= 2 \end{align*}

Use the gradient to determine the angle of inclination of the line

\begin{align*} \tan \theta &= m \\ &= 2\\ \therefore \theta &= \tan^{-1}2\\ &= \text{63,4}\text{°} \end{align*}

Important: make sure your calculator is in DEG (degrees) mode.

Write the final answer

The angle of inclination of the straight line is \(\text{63,4}\)\(\text{°}\).

temp text

Worked example 9: Inclination of a straight line

Determine the equation of the straight line passing through the point \((3;1)\) and with an angle of inclination of \(\text{135}\text{°}\).

Use the angle of inclination to determine the gradient of the line

\begin{align*} m &= \tan \theta \\ &= \tan \text{135}\text{°} \\ \therefore m &= -1 \end{align*}

Write down the gradient–point form of the straight line equation

\[y - y_1 = m(x - x_1)\]

Substitute \(m = -1\)

\[y - y_1 = -(x - x_1)\]

Substitute the given point \((3;1)\)

\begin{align*} y - 1 & = -(x - 3) \\ y & = -x + 3 +1 \\ &= -x + 4 \end{align*}

Write the final answer

The equation of the straight line is \(y = -x + 4\).

temp text

Worked example 10: Inclination of a straight line

Determine the acute angle (correct to \(\text{1}\) decimal place) between the line passing through the points \(M(-1;1\frac{3}{4})\) and \(N(4;3)\) and the straight line \(y = - \frac{3}{2}x + 4\).

Draw a sketch

Draw the line through points \(M(-1;1\frac{3}{4})\) and \(N(4;3)\) and the line \(y = - \frac{3}{2}x + 4\) on a suitable system of axes. Label \(\alpha\) and \(\beta\), the angles of inclination of the two lines. Label \(\theta\), the acute angle between the two straight lines.

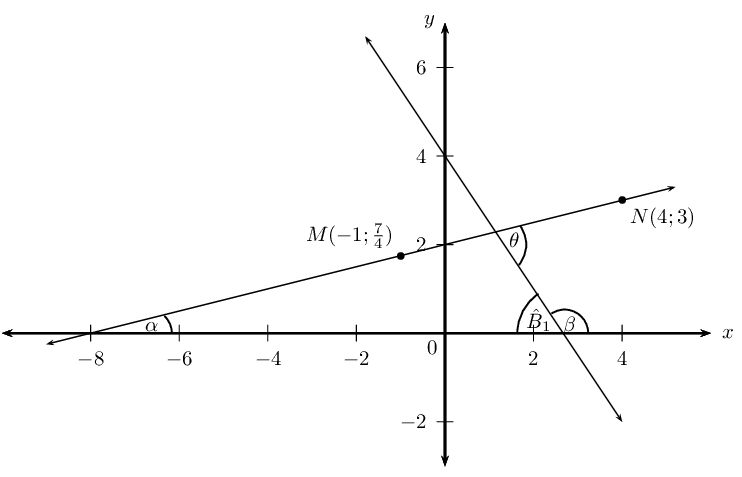
Notice that \(\alpha\) and \(\theta\) are acute angles and \(\beta\) is an obtuse angle.

\[\begin{array}{rll} \hat{B}_1 &= \text{180}\text{°} - \beta & (\angle \text{ on str. line}) \\ \text{and } \theta &= \alpha + \hat{B}_1 \quad & (\text{ext. } \angle \text{ of } \triangle = \text{ sum int. opp}) \\ \therefore \theta &= \alpha + (\text{180}\text{°} - \beta) \\ &= \text{180}\text{°} + \alpha - \beta \end{array}\]

Use the gradient to determine the angle of inclination \(\beta\)

From the equation \(y = -\frac{3}{2}x + 4\) we see that \(m < 0\), therefore \(\beta\) is an obtuse angle such that \(\text{90}\text{°} < \beta < \text{180}\text{°}\).

\begin{align*} \tan \beta &= m\\ &= -\frac{3}{2} \\ \tan^{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°} \end{align*}

This negative angle lies in the fourth quadrant. We know that the angle of inclination \(\beta\) is an obtuse angle that lies in the second quadrant, therefore

\begin{align*} \beta &= -\text{56,3}\text{°} + \text{180}\text{°}\\ &= \text{123,7}\text{°} \end{align*}

Determine the gradient and angle of inclination of the line through \(M\) and \(N\)

Determine the gradient \begin{align*} m & = \frac{y_2 - y_1}{x_2 - x_1} \\ & = \dfrac{3 - \frac{7}{4}}{4-(-1)} \\ & = \dfrac{\frac{5}{4}}{5} \\ &= \frac{1}{4} \end{align*}

Determine the angle of inclination \begin{align*} \tan \alpha & = m\\ & = \frac{1}{4} \\ \therefore \alpha & = \tan^{-1} \left( \frac{1}{4} \right) \\ &= \text{14,0}\text{°} \end{align*}

Write the final answer

\begin{align*} \theta & = \text{180}\text{°} + \alpha - \beta \\ & = \text{180}\text{°} + \text{14,0}\text{°} - \text{123,7}\text{°} \\ & = \text{70,3}\text{°} \end{align*}

The acute angle between the two straight lines is \(\text{70,3}\)\(\text{°}\).

temp text

Inclination of a straight line

Textbook Exercise 4.6

a line with \(m = \dfrac{4}{5}\)

\begin{align*} m &= \frac{4}{5} \\ \theta &= \tan^{-1} \left( \frac{4}{5} \right) \\ \therefore \theta &= \text{38,7}\text{°} \end{align*}

\(x + y + 1 = 0\)

\begin{align*} x + y + 1 &= 0 \\ y &= -x - 1\\ m &= -1 \\ \theta &= \tan^{-1} \left( -1 \right) \\ &= -\text{45}\text{°} \\ \therefore \theta &= \text{180}\text{°} - \text{45}\text{°} \\ \therefore \theta &= \text{135}\text{°} \end{align*}

a line with \(m = \text{5,69}\)

\begin{align*} m &= \text{5,69} \\ \theta &= \tan^{-1} \left( \text{5,69} \right) \\ \therefore \theta &= \text{80}\text{°} \end{align*}

the line that passes through \((1;1)\) and \((-2;7)\)

\begin{align*} m &= \frac{y_2 -y_1}{x_2 - x_1} \\ &= \frac{7-1}{-2-1} \\ &= \frac{6}{-3} \\ \therefore m &= -\text{2} \\ \theta &= \tan^{-1} \left( -\text{2} \right) \\ &= -\text{63,4}\text{°} \\ \therefore \theta &= \text{180}\text{°} - \text{63,4}\text{°} \\ \therefore \theta &= \text{80}\text{°} \end{align*}

\(3 - 2y = 9x\)

\begin{align*} 3 - 2y &= 9x \\ 3 - 9x &= 2y \\ \frac{3}{2} - \frac{9}{2}x &= y \\ \therefore m &= - \frac{9}{2} \\ \theta &= \tan^{-1} \left( - \frac{9}{2} \right) \\ &= -\text{77,5}\text{°} \\ \therefore \theta &= \text{180}\text{°} - \text{77,5}\text{°} \\ \therefore \theta &= \text{102,5}\text{°} \end{align*}

the line that passes through \((-1;-6)\) and \((-\frac{1}{2};-\frac{11}{2})\)

\begin{align*} m &= \frac{y_2 -y_1}{x_2 - x_1} \\ &= \frac{-\frac{11}{2}+ 6}{-\frac{1}{2}+1} \\ &= \frac{\frac{1}{2}}{\frac{1}{2}} \\ \therefore m &= 1 \\ \theta &= \tan^{-1} \left( 1 \right) \\ \therefore \theta &= \text{45}\text{°} \end{align*}

\(5 = 10y - 15x\)

\begin{align*} 5 &= 10y - 15x \\ 5 + 15x &= 10y \\ \frac{1}{2} + \frac{3}{2}x &= y \\ \therefore m &= \frac{3}{2} \\ \theta &= \tan^{-1} \left( \frac{3}{2} \right) \\ \therefore \theta &= \text{56,3}\text{°} \end{align*}

\begin{align*} m &= \frac{y_2 -y_1}{x_2 - x_1} \\ &= \frac{3 + 1}{2 - 0} \\ &= \frac{4}{2} \\ \therefore m &= 2 \\ \theta &= \tan^{-1} \left( 2 \right) \\ \therefore \theta &= \text{63,4}\text{°} \end{align*}

\begin{align*} m &= \frac{y_2 -y_1}{x_2 - x_1} \\ &= \frac{2 - 0}{0 - 6} \\ &= \frac{2}{-6} \\ \therefore m &= -\frac{1}{3} \\ \theta &= \tan^{-1} \left( -\frac{1}{3} \right) \\ \therefore \theta &= -\text{18,4}\text{°} \\ \therefore \theta &= \text{180}\text{°} - \text{18,4}\text{°} \\ \therefore \theta &= \text{161,6}\text{°} \end{align*}

Gradient undefined

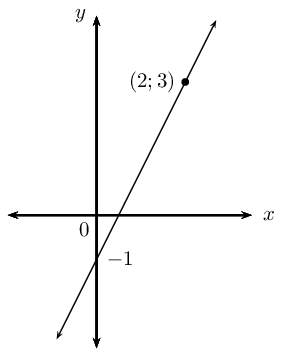
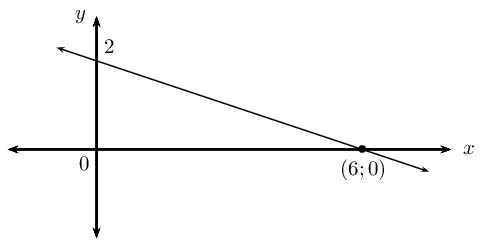
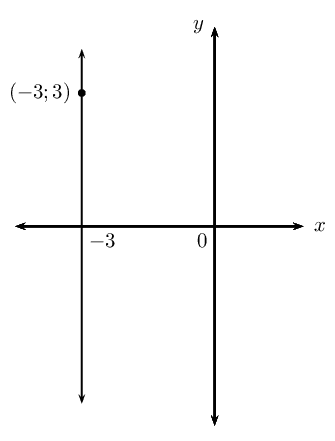
Determine the acute angle between the line passing through the points \(A(-2;\frac{1}{5})\) and \(B(0;1)\) and the line passing through the points \(C(1;0)\) and \(D(-2;6)\).

Let the angle of inclination for the line \(AB\) be \(\beta\) and let the angle of inclination for the line \(CD\) be \(\alpha\). Let the angle between the two lines be \(\theta\):

\begin{align*} m_{AB} &= \frac{y_2 -y_1}{x_2 - x_1} \\ &= \frac{1 - \frac{1}{5}}{0 + 2} \\ &= \frac{\frac{4}{5}}{2} \\ \therefore m &= \frac{4}{10} \\ &= \frac{2}{5} \\ \beta &= \tan^{-1} \left( \frac{2}{5} \right) \\ \therefore \beta &= \text{21,8}\text{°} \\ m_{CD} &= \frac{y_2 -y_1}{x_2 - x_1} \\ &= \frac{6 - 0}{-2-1} \\ &= \frac{6}{-3} \\ \therefore m &= -2 \\ \alpha &= \tan^{-1} \left( -2 \right) \\ \therefore \alpha &= -\text{63,4}\text{°} \\ \therefore \alpha &= \text{180}\text{°} - \text{63,4}\text{°} \\ \therefore \alpha &= \text{116,6}\text{°} \\ \text{And } \theta &= \beta + (\text{180}\text{°} - \alpha) \quad (\text{ext. } \angle \triangle) \\ \therefore \theta &= \text{21,8}\text{°} + (\text{180}\text{°} - \text{116,6}\text{°} ) \\ &= \text{85,2}\text{°} \end{align*}

Determine the angle between the line \(y + x = 3\) and the line \(x = y + \frac{1}{2}\).

Let the angle of inclination for the line \(y + x = 3\) be \(\alpha\) and let the angle of inclination for the line \(x = y + \frac{1}{2}\) be \(\beta\). Let the angle between the two lines be \(\theta\):

\begin{align*} y &= - x + 3 \\ \therefore m &= - 1 \\ \alpha &= \tan^{-1} \left( -1\right) \\ \therefore \alpha &= -\text{45}\text{°} \\ \therefore \alpha &= \text{180}\text{°} - \text{45}\text{°} \\ \therefore \alpha &= \text{135}\text{°} \\ x &= y + \frac{1}{2} \\ x - \frac{1}{2} &= y \\ \therefore m &= 1 \\ \beta &= \tan^{-1} \left(1 \right) \\ \therefore \beta &= \text{45}\text{°} \\ \text{And } \theta &= \beta + (\text{180}\text{°} - \alpha) \quad (\text{ext. } \angle \triangle) \\ \therefore \theta &= \text{45}\text{°} + (\text{180}\text{°} - \text{135}\text{°} ) \\ &= \text{90}\text{°} \end{align*}

Find the angle between the line \(y = 2x\) and the line passing through the points \((-1;\frac{7}{3})\) and \((0;2)\).

Let the angle of inclination for the line \(y = 2x\) be \(\beta\) and let the angle of inclination for the other line be \(\alpha\). Let the angle between the two lines be \(\theta\):

\begin{align*} y &= 2x \\ \therefore m &= 2 \\ \beta &= \tan^{-1} \left( 2 \right) \\ \therefore \beta &= \text{63,4}\text{°} \\ m &= \frac{y_2 -y_1}{x_2 - x_1} \\ &= \frac{2 - \frac{7}{3}}{0 + 1} \\ &= \frac{-\frac{1}{3}}{1} \\ \therefore m &= -\frac{1}{3} \\ \therefore \alpha &= -\text{18,4}\text{°} \\ \therefore \alpha &= \text{180}\text{°} - \text{18,4}\text{°} \\ \therefore \alpha &= \text{161,6}\text{°} \\ \text{And } \theta &= \beta + (\text{180}\text{°} - \alpha) \quad (\text{ext. } \angle \triangle) \\ \therefore \theta &= \text{63,4}\text{°} + (\text{180}\text{°} - \text{161,6}\text{°} ) \\ &= \text{81,8}\text{°} \end{align*}

4.2 Equation of a line

Table of Contents

4.4 Parallel lines