\((3;7)\) and \((-6;1)\)
4.2 Equation of a line
|
Previous
4.1 Revision
|
Next
4.3 Inclination of a line
|
4.2 Equation of a line (EMBG8)
We can derive different forms of the straight line equation. The different forms are used depending on the information provided in the problem:
- The two-point form of the straight line equation: \(\dfrac{y-y_1}{x-x_1} = \dfrac{y_2-y_1}{x_2-x_1}\)
- The gradient–point form of the straight line equation: \(y-y_1 = m(x-x_1)\)
- The gradient–intercept form of the straight line equation: \(y = mx + c\)
The two-point form of the straight line equation (EMBG9)
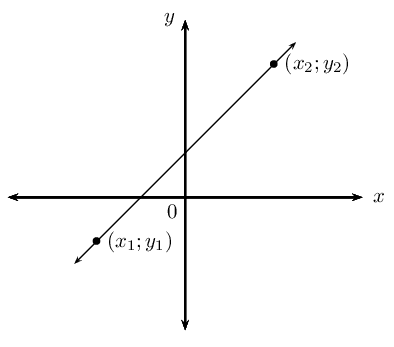
Given any two points \(\left({x}_{1};{y}_{1}\right)\) and \(\left({x}_{2};{y}_{2}\right)\), we can determine the equation of the line passing through the two points using the equation:
\[\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\]
Worked example 3: The two-point form of the straight line equation
Find the equation of the straight line passing through \(P\left(-1;-5\right)\) and \(Q\left(5;4\right)\).
Draw a sketch
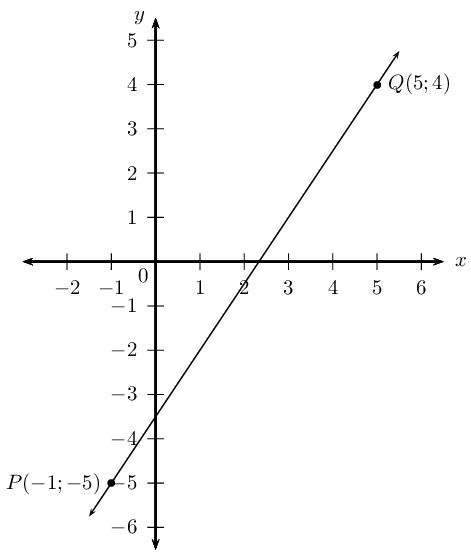
Assign variables to the coordinates of the given points
Let the coordinates of \(P\) be \((x_1;y_1)\) and \(Q(x_2;y_2)\)
\[x_1 = -1; \qquad y_1 = -5; \qquad x_2 = 5; \qquad y_2 = 4\]
Write down the two-point form of the straight line equation
\[\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\]
Substitute the values and make \(y\) the subject of the equation
\begin{align*} \frac{y-(-5)}{x-(-1)} &= \frac{4-(-5)}{5-(-1)} \\ \frac{y+5}{x+1} &= \frac{9}{6} \\ y+5 &= \frac{3}{2}(x+1) \\ y+5 &= \frac{3}{2}x + \frac{3}{2} \\ y &= \frac{3}{2}x - \frac{7}{2} \end{align*}
Write the final answer
\[y = \frac{3}{2}x - 3\frac{1}{2}\]
The two-point form of the straight line equation
Determine the equation of the straight line passing through the points:
\((1;-\frac{11}{4})\) and \((\frac{2}{3}; -\frac{7}{4})\)
\((-2;1)\) and \((3;6)\)
\((2;3)\) and \((3;5)\)
\((1;-5)\) and \((-7;-5)\)
\((-4;0)\) and \((1;\frac{15}{4})\)
\((s;t)\) and \((t;s)\)
\((-2;-8)\) and \((1;7)\)
\((2p;q)\) and \((0;-q)\)
The gradient–point form of the straight line equation (EMBGB)
We derive the gradient–point form of the straight line equation using the definition of gradient and the two-point form of a straight line equation \[\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\]
Substitute \(m = \dfrac{y_2-y_1}{x_2-x_1}\) on the right-hand side of the equation \[\frac{y-y_1}{x-x_1} = m\]
Multiply both sides of the equation by \((x-x_1)\) \[y-y_1 = m(x-x_1)\]
To use this equation, we need to know the gradient of the line and the coordinates of one point on the line.
Worked example 4: The gradient–point form of the straight line equation
Determine the equation of the straight line with gradient \(m = -\frac{1}{3}\) and passing through the point \((-1;1)\).
Draw a sketch
We notice that \(m < 0\), therefore the graph decreases as \(x\) increases.
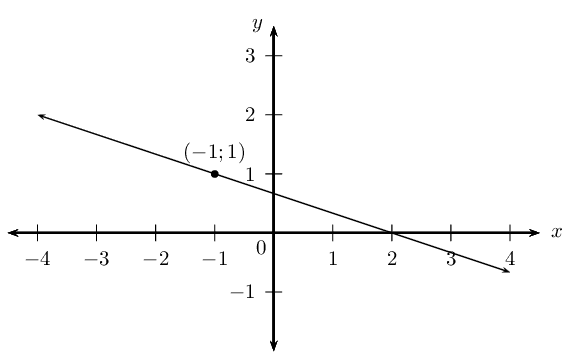
Write down the gradient–point form of the straight line equation
\[y - y_1= m(x - x_1)\]
Substitute the value of the gradient
\[y - y_1= -\frac{1}{3}(x - x_1)\]
Substitute the coordinates of the given point
\begin{align*} y - 1 &= -\frac{1}{3}(x - (-1)) \\ y - 1 &= -\frac{1}{3}(x + 1) \\ y &= -\frac{1}{3}x - \frac{1}{3} + 1\\ &= -\frac{1}{3}x + \frac{2}{3} \end{align*}
Write the final answer
The equation of the straight line is \(y = -\frac{1}{3}x +\frac{2}{3}\).
If we are given two points on a straight line, we can also use the gradient–point form to determine the equation of a straight line. We first calculate the gradient using the two given points and then substitute either of the two points into the gradient–point form of the equation.
Worked example 5: The gradient–point form of the straight line equation
Determine the equation of the straight line passing through \(\left(-3;2\right)\) and \(\left(5;8\right)\).
Draw a sketch
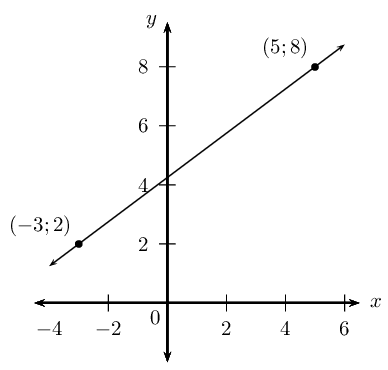
Assign variables to the coordinates of the given points
\[x_1 = -3; \qquad y_1 = 2; \qquad x_2 = 5; \qquad y_2 = 8\]
Calculate the gradient using the two given points
\begin{align*} m &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{8 - 2}{5 - (- 3)} \\ &= \frac{6}{8} \\ &= \frac{3}{4} \end{align*}
Write down the gradient–point form of the straight line equation
\[y - y_1= m(x - x_1)\]
Substitute the value of the gradient
\[y - y_1= \frac{3}{4}(x - x_1)\]
Substitute the coordinates of a given point
\begin{align*} y - y_1 &= \frac{3}{4}(x - x_1) \\ y - 2 &= \frac{3}{4}(x - (-3)) \\ y - 2 &= \frac{3}{4}(x + 3) \\ y &= \frac{3}{4}x + \frac{9}{4} + 2\\ &= \frac{3}{4}x + \frac{17}{4} \end{align*}
Write the final answer
The equation of the straight line is \(y = \frac{3}{4}x +4\frac{1}{4}\).
Gradient–point form of a straight line equation
Determine the equation of the straight line:
passing through the point \((-1;\frac{10}{3})\) and with \(m=\frac{2}{3}\).
with \(m= -1\) and passing through the point \((-2;0)\).
passing through the point \((3;-1)\) and with \(m=-\frac{1}{3}\).
parallel to the \(x\)-axis and passing through the point \((0;11)\).
passing through the point \((1;5)\) and with \(m=-2\).
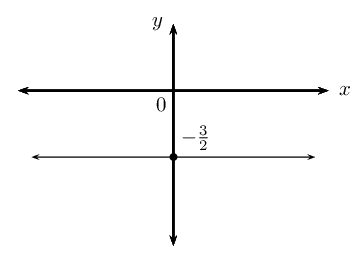
perpendicular to the \(x\)-axis and passing through the point \((-\frac{3}{2};0)\).
with \(m = -\text{0,8}\) and passing through the point \((10;-7)\).
with undefined gradient and passing through the point \((4;0)\).
with \(m= 3a\) and passing through the point \((-2;-6a+b)\).
The gradient–intercept form of a straight line equation (EMBGC)
Using the gradient–point form, we can also derive the gradient–intercept form of the straight line equation.
Starting with the equation
\[y - y_1 = m(x - x_1)\]
Expand the brackets and make \(y\) the subject of the formula
\begin{align*} y - y_1 &= mx - mx_1 \\ y &= mx - mx_1 + y_1 \\ y &= mx + (y_1 - mx_1) \end{align*}We define constant \(c\) such that \(c={y}_{1}-m{x}_{1}\) so that we get the equation
\[y = mx + c\]
This is also called the standard form of the straight line equation.
Notice that when \(x=0\), we have
\begin{align*} y &= m(0) + c \\ &= c \end{align*}Therefore \(c\) is the \(y\)-intercept of the straight line.
Worked example 6: The gradient–intercept form of straight line equation
Determine the equation of the straight line with gradient \(m=-2\) and passing through the point \((-1;7)\).
Slope of the line
We notice that \(m < 0\), therefore the graph decreases as \(x\) increases.
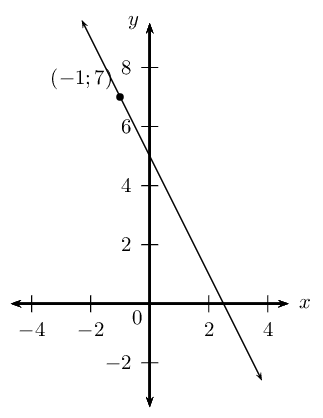
Write down the gradient–intercept form of straight line equation
\[y =mx + c\]
Substitute the value of the gradient
\[y = -2x + c\]
Substitute the coordinates of the given point and find \(c\)
\begin{align*} y &= -2x + c \\ 7 &= -2(-1) + c \\ 7 - 2 &= c \\ \therefore c &= 5 \end{align*}This gives the \(y\)-intercept \((0;5)\).
Write the final answer
The equation of the straight line is \(y = -2x + 5\).
If we are given two points on a straight line, we can also use the gradient–intercept form to determine the equation of a straight line. We solve for the two unknowns \(m\) and \(c\) using simultaneous equations — using the methods of substitution or elimination.
Worked example 7: The gradient–intercept form of straight line equation
Determine the equation of the straight line passing through the points \((-2;-7)\) and \((3;8)\).
Draw a sketch
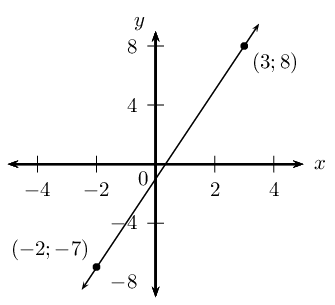
Write down the gradient–intercept form of straight line equation
\[y =mx + c\]
Substitute the coordinates of the given points
\[\begin{array}{rll} -7 & = m(-2) + c & \\ -7 & = -2m + c & \ldots (1) \\ \\ 8 & = m(3) + c & \\ 8 & = 3m + c & \ldots (2) \end{array}\]We have two equations with two unknowns; we can therefore solve using simultaneous equations.
Make the coefficient of one of the variables the same in both equations
We notice that the coefficient of \(c\) in both equations is \(\text{1}\), therefore we can subtract one equation from the other to eliminate \(c\):
\begin{align*} -7 &= -2m + c \\ -( 8 &= 3m + c ) \\ -15 &= -5m \\ \therefore 3 &= m \end{align*}Substitute \(m=3\) into either of the two equations and determine \(c\): \begin{align*} -7 &= -2m + c \\ -7 &= -2(3) + c \\ \therefore c &= -1 \end{align*} or \begin{align*} 8 &= 3m + c \\ 8 &= 3(3) + c \\ \therefore c &= -1 \end{align*}
Write the final answer
The equation of the straight line is \(y = 3x - 1\).
The gradient–intercept form of a straight line equation
Determine the equation of the straight line:
passing through the point \((\frac{1}{2};4)\) and with \(m=2\).
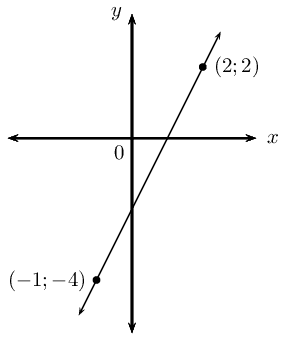
passing through the points \((\frac{1}{2};-2)\) and \((2;4)\).
passing through the points \((2;-3)\) and \((-1;0)\).
passing through the point \((2;-\frac{6}{7})\) and with \(m=-\frac{3}{7}\).
which cuts the \(y\)-axis at \(y=-\frac{1}{5}\) and with \(m=\frac{1}{2}\).
|
Previous
4.1 Revision
|
Table of Contents |
Next
4.3 Inclination of a line
|
