6.3 Quadratic functions

Functions of the form \(y={x}^{2}\) (EMA4J)

Functions of the general form \(y=a{x}^{2}+q\) are called parabolic functions. In the equation \(y=a{x}^{2}+q\), \(a\) and \(q\) are constants and have different effects on the parabola.

Worked example 4: Plotting a quadratic function

\(y=f(x)={x}^{2}\)

Complete the following table for \(f(x)={x}^{2}\) and plot the points on a system of axes.

\(x\)	\(-\text{3}\)	\(-\text{2}\)	\(-\text{1}\)	\(\text{0}\)	\(\text{1}\)	\(\text{2}\)	\(\text{3}\)
\(f(x)\)	\(\text{9}\)

1. Join the points with a smooth curve.

2. The domain of \(f\) is \(x\in \mathbb{R}\). Determine the range.

3. About which line is \(f\) symmetrical?

4. Determine the value of \(x\) for which \(f(x)=6\frac{1}{4}\). Confirm your answer graphically.

5. Where does the graph cut the axes?

Substitute values into the equation

\begin{align*} f(x) & = {x}^{2} \\ f(-3) & = {(-3)}^{2} = 9\\ f(-2) & = {(-2)}^{2} = 4\\ f(-1) & = {(-1)}^{2} = 1\\ f(0) & = {(0)}^{2} = 0\\ f(1) & = {(1)}^{2} = 1\\ f(2) & = {(2)}^{2} = 4\\ f(3) & = {(3)}^{2} = 9 \end{align*}

\(x\)	\(-\text{3}\)	\(-\text{2}\)	\(-\text{1}\)	\(\text{0}\)	\(\text{1}\)	\(\text{2}\)	\(\text{3}\)
\(f(x)\)	\(\text{9}\)	\(\text{4}\)	\(\text{1}\)	\(\text{0}\)	\(\text{0}\)	\(\text{4}\)	\(\text{9}\)

Plot the points and join with a smooth curve

From the table, we get the following points:

\((-3;9), (-2;4), (-1;1), (0;0), (1;1), (2;4), (3;9)\)

Determine the domain and range

Domain: \(x\in \mathbb{R}\)

From the graph we see that for all values of \(x\), \(y \ge 0\).

Range: \(\left\{y:y\in \mathbb{R}, y\ge 0\right\}\)

Find the axis of symmetry

\(f\) is symmetrical about the \(y\)-axis. Therefore the axis of symmetry of \(f\) is the line \(x=0\).

Determine the \(x\)-value for which \(f(x)=6\frac{1}{4}\)

\begin{align*} f(x)& = \frac{25}{4} \\ \therefore \frac{25}{4}& = {x}^{2} \\ x& = ±\frac{5}{2}\\ & = ±2\frac{1}{2} \end{align*}

See points \(A\) and \(B\) on the graph.

Determine the intercept

The function \(f\) intercepts the axes at the origin \((0;0)\).

We notice that as the value of \(x\) increases from \(-\infty\) to \(\text{0}\), \(f(x)\) decreases.

At the turning point \((0;0)\), \(f(x)=0\).

As the value of \(x\) increases from \(\text{0}\) to \(∞\), \(f(x)\) increases.

Functions of the form \(y=a{x}^{2}+q\) (EMA4K)

The effect of \(q\)

The effect of \(q\) is called a vertical shift because all points are moved the same distance in the same direction (it slides the entire graph up or down).

• For \(q>0\), the graph of \(f(x)\) is shifted vertically upwards by \(q\) units. The turning point of \(f(x)\) is above the \(y\)-axis.

• For \(q<0\), the graph of \(f(x)\) is shifted vertically downwards by \(q\) units. The turning point of \(f(x)\) is below the \(y\)-axis.

The effect of \(a\)

The sign of \(a\) determines the shape of the graph.

• For \(a>0\), the graph of \(f(x)\) is a “smile” and has a minimum turning point at \((0;q)\). The graph of \(f(x)\) is stretched vertically upwards; as \(a\) gets larger, the graph gets narrower.

  For \(0<a<1\), as \(a\) gets closer to \(\text{0}\), the graph of \(f(x)\) gets wider.

• For \(a<0\), the graph of \(f(x)\) is a “frown” and has a maximum turning point at \((0;q)\). The graph of \(f(x)\) is stretched vertically downwards; as \(a\) gets smaller, the graph gets narrower.

  For \(-1<a<0\), as \(a\) gets closer to \(\text{0}\), the graph of \(f(x)\) gets wider.

	\(a<0\)	\(a>0\)
\(q>0\)
\(q=0\)
\(q<0\)

Table 6.2: The effect of \(a\) and \(q\) on a parabola.

Discovering the characteristics (EMA4M)

The standard form of the equation of a parabola is \(y=a{x}^{2}+q\).

Sketching graphs of the form \(y=a{x}^{2}+q\) (EMA4N)

In order to sketch graphs of the form \(f(x)=a{x}^{2}+q\), we need to determine the following characteristics:

1. sign of \(a\)

2. \(y\)-intercept

3. \(x\)-intercept

4. turning point

Worked example 6: Sketching a parabola

Sketch the graph of \(y={2x}^{2}-4\). Mark the intercepts and turning point.

Examine the standard form of the equation

We notice that \(a>0\). Therefore the graph is a “smile” and has a minimum turning point.

Calculate the intercepts

For the \(y\)-intercept, let \(x=0\):

\begin{align*} y& = 2{x}^{2}-4 \\ & = 2{(0)}^{2}-4 \\ & =-4 \end{align*}

This gives the point \((0;-4)\).

For the \(x\)-intercepts, let \(y=0\):

\begin{align*} y& = 2{x}^{2}-4 \\ 0& = 2{x}^{2}-4 \\ {x}^{2}& = 2 \\ \therefore x& = ±\sqrt{2} \end{align*}

This gives the points \((-\sqrt{2};0)\) and \((\sqrt{2};0)\).

Determine the turning point

From the standard form of the equation we see that the turning point is \((0;-4)\).

Plot the points and sketch the graph

Domain: \(\left\{x:x\in \mathbb{R}\right\}\)

Range: \(\left\{y:y\ge -4,y\in \mathbb{R}\right\}\)

The axis of symmetry is the line \(x=0\).

Worked example 7: Sketching a parabola

Sketch the graph of \(g(x)=-\frac{1}{2}{x}^{2}-3\). Mark the intercepts and the turning point.

Examine the standard form of the equation

We notice that \(a<0\). Therefore the graph is a “frown” and has a maximum turning point.

Calculate the intercepts

For the \(y\)-intercept, let \(x=0\):

\begin{align*} g(x)& = -\frac{1}{2}{x}^{2}-3 \\ g(0)& = -\frac{1}{2}{(0)}^{2}-3 \\ & = -3 \end{align*}

This gives the point \((0;-3)\).

For the \(x\)-intercepts let \(y=0\):

\begin{align*} 0& = -\frac{1}{2}{x}^{2}-3 \\ 3& = -\frac{1}{2}{x}^{2} \\ -2(3)& = {x}^{2} \\ -6& = {x}^{2} \end{align*}

There is no real solution, therefore there are no \(x\)-intercepts.

Determine the turning point

From the standard form of the equation we see that the turning point is \((0;-3)\).

Plot the points and sketch the graph

Domain: \(x\in \mathbb{R}\).

Range: \(y\in \left(-\infty ;-3\right]\).

The axis of symmetry is the line \(x=0\).

Textbook Exercise 6.3

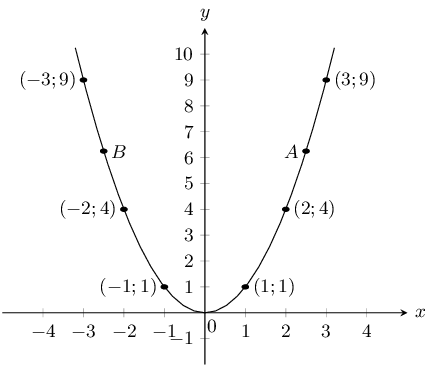
The graph below shows a quadratic function with the following form: \(y = ax^2 + q\). Two points on the parabola are shown: Point A, the turning point of the parabola, at \((0;4)\), and Point B is at \(\left(2; \frac{8}{3}\right)\). Calculate the values of \(a\) and \(q\).

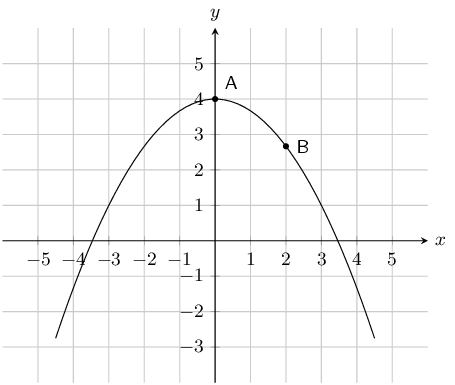
The value of \(q\) is 4.

\begin{align*} y & = ax^2 +4 \\ \left( \frac{8}{3} \right) & = a(\text{2})^2 +4 \quad \longleftarrow \quad ^{\text{substitute in the}}_{\text{coordinates of a point!}} \\ \frac{8}{3} & = \text{4}a +4 \\ \frac{8}{3} -4 & = \text{4}a \\ - \frac{4}{3} & = \text{4}a \\ - \frac{1}{3} & = a \end{align*} \[a = - \frac{1}{3};~ q = 4\]

The graph below shows a quadratic function with the following form: \(y = ax^2 + q\). Two points on the parabola are shown: Point A, the turning point of the parabola, at \((0;-3)\), and Point B is at \(\left(2; 5\right)\). Calculate the values of \(a\) and \(q\).

The value of \(q\) is -3.

\begin{align*} y & = ax^2 -3 \\ \left( 5 \right) & = a(\text{2})^2 -3 \quad \longleftarrow \quad ^{\text{substitute in the}}_{\text{coordinates of a point!}} \\ 5 & = \text{4}a -3 \\ 5 +3 & = \text{4}a \\ 8 & = \text{4}a \\ 2 & = a \end{align*} \[a = 2;~ q = -3\]

Given the following equation:

\(y=5 x^{2} - 2\)

Calculate the \(y\)-coordinate of the \(y\)-intercept.

\begin{align*} y & = ax^2 + q \\ & = 5 x^{2} - 2 \\ & = 5 (0)^{2} - 2\\ & = 0-2 \end{align*}

The \(y\)-coordinate of the \(y\)-intercept is \(-2\).

Now calculate the \(x\)-intercepts. Your answer must be correct to 2 decimal places.

\begin{align*} y & = 5 x^{2} - 2 \\ (0) & =5 x^{2} - 2 \\ - 5 x^{2} &=-2\\ x^2 &= \frac{-2}{-5} \\ x & =\pm \sqrt{\frac{2}{5}}\\ \text{Therefore: } x = +\sqrt{\frac{2}{5}} &\text{ and } x = - \sqrt{\frac{2}{5}} \\ x= -\text{0,63} &\text{ and } x= \text{0,63} \end{align*}

The \(x\)-intercepts are \((-\text{0,63};0)\) and \((\text{0,63};0)\).

Given the following equation:

\(y=- 2 x^{2} + 1\)

Calculate the \(y\)-coordinate of the \(y\)-intercept.

\begin{align*} y & = ax^2 + q \\ & = - 2 x^{2} + 1 \\ & = - 2 (0)^{2} + 1\\ & = 0 + 1 \end{align*}

The \(y\)-coordinate of the \(y\)-intercept is \(\text{1}\).

Now calculate the \(x\)-intercepts. Your answer must be correct to 2 decimal places.

\begin{align*} y & = - 2 x^{2} + 1 \\ (0) & =- 2 x^{2} + 1 \\ 2 x^{2} &=1\\ x^2 &= \frac{1}{2} \\ x & =\pm \sqrt{\frac{1}{2}}\\ \text{Therefore: } x = +\sqrt{\frac{1}{2}} &\text{ and } x = - \sqrt{\frac{1}{2}} \\ x= -\text{0,71} & \text{ and } x\end{align*}

The \(x\)-intercepts are \((-\text{0,71};0)\) and \((\text{0,71};0)\).

Given the following graph, identify a function that matches each of the following equations:

\(y = \text{0,5}x^2\)

\(h(x)\)

\(y = x^2\)

\(g(x)\)

\(y = 3x^2\)

\(f(x)\)

\(y = -x^2\)

\(k(x)\)

Given the following graph, identify a function that matches each of the following equations:

\(y = x^2 - 3\)

\(h(x)\)

\(y = x^2 + 1\)

\(f(x)\)

\(y = x^2\)

\(g(x)\)

Two parabolas are drawn: \(g: y=ax^2+p\) and \(h:y=bx^2+q\).

Find the values of \(a\) and \(p\).

\(p\) is the \(y\)-intercept of the function \(g(x)\), therefore \(p=-9\)

To find \(a\) we use one of the points on the graph (e.g. \((4;7)\)):

\begin{align*} y&=ax^2-9\\ 7&= a(4^2) - 9\\ 16a&=16\\ \therefore a&=1 \end{align*}

\(a=1\); \(p=-9\)

Find the values of \(b\) and \(q\).

\(q\) is the \(y\)-intercept of the function \(h(x)\), therefore \(q = 23\)

To find \(b\), we use one of the points on the graph (e.g. \((4;7)\)):

\begin{align*} y&=bx^{2} =23\\ 7&= b(4^{2}) +23\\ 16b&=-16\\ \therefore b&=-1 \end{align*}

\(b=-1\); \(q=23\)

Find the values of \(x\) for which \(g(x) \geq h(x)\).

These are the points where \(g\) lies above \(h\).

From the graph we see that \(g\) lies above \(h\) when: \(x \le -4\) or \(x \geq 4\)

For what values of \(x\) is \(g\) increasing?

\(g\) increases from the turning point \((0;-9)\), i.e. for \(x \geq 0\).

Show that if \(a < 0\) the range of \(f(x)=ax^2 + q\) is \(\left\{f(x):f(x) \le q\right\}\).

Because the square of any number is always positive we get: \(x^2 \geq 0\).

If we multiply by \(a\) where \((a < 0)\) then the sign of the inequality is reversed: \(ax^2 \le 0\)

Adding \(q\) to both sides gives \(ax^2 + q \le q\)

And so \(f(x) \le q\)

This gives the range as \((-\infty; q]\).

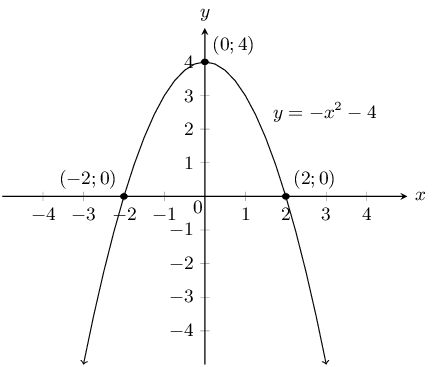
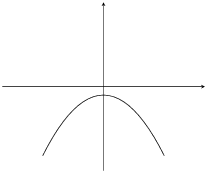
Draw the graph of the function \(y=-x^2 + 4\) showing all intercepts with the axes.

The \(y\)-intercept is \((0;4)\). The \(x\)-intercepts are given by setting \(y = 0\):

\begin{align*} 0 & = -x^2 + 4 \\ x^2 & = 4 \\ x & = \pm 2 \end{align*}

Therefore the \(x\)-intercepts are: \((2;0)\) and \((-2;0)\).

Now we can sketch the graph: