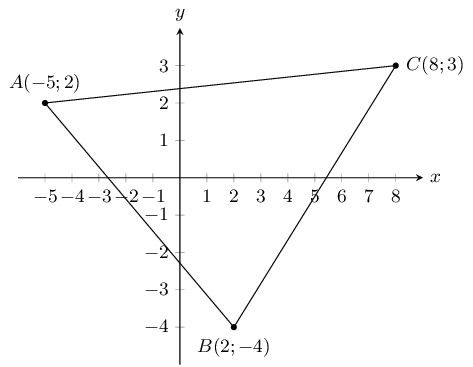
Prove that triangle \(ABC\) is a right-angled triangle.
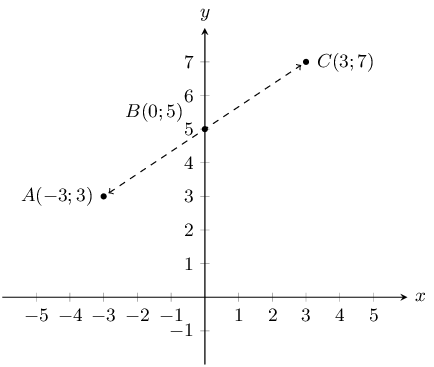
We first draw a sketch:

To show that \(\triangle ABC\) is right angled we need to show that \(AB \perp AC\) or that \(AC
\perp BC\) or \(AB \perp BC\). We can do this by calculating the gradients of \(AB\), \(AC\) and
\(BC\) and then seeing if any of these gradients is the negative inverse of any of the other two
gradients.
\begin{align*}
m_{AB} & = \frac{-2 - 1}{3 - (-3)} \\
& = \frac{-3}{6} \\
& = \frac{-1}{2} \\\\
m_{BC} & = \frac{10 - (-2)}{9 - 3} \\
& = \frac{12}{6} \\
& = 2 \\\\
m_{AC} & = \frac{10 - 1}{9 - (-3)} \\
& = \frac{9}{12} \\
& = \frac{3}{4}
\end{align*}
Now we note that:
\begin{align*}
m_{AB} \times m_{BC} & = \frac{-1}{2} \times 2 = -1 \\
\therefore AB \perp BC \\
\therefore \triangle ABC \text{ is right-angled}
\end{align*}
Find the coordinates of \(D\), if \(ABCD\) is a parallelogram.
A parallelogram has both sides equal in length and parallel. Therefore \(CD \parallel AB\) and \(AD
\parallel BC\). Also \(CD = AB\) and \(AD = BC\).
Let the coordinates of \(D\) be \((x;y)\).
Since \(AD \parallel BC\), \(m_{AD} = m_{BC}\).
From the previous question we know that \(m_{BC} = 2\). Therefore the gradient of \(AD\) is:
\begin{align*}
m_{AD} & = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\
2 & = \frac{y - 1}{x - (-3)} \\
2(x + 3) & = y - 1 \\
2x + 6 & = y - 1 \\
2x + 7 & = y
\end{align*}
Since \(CD \parallel AB\), \(m_{CD} = m_{AB}\).
From the previous question we know that \(m_{AB} = \frac{-1}{2}\). Therefore the gradient of \(CD\)
is:
\begin{align*}
m_{CD} & = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\
\frac{-1}{2} & = \frac{y - 10}{x - 9} \\
\frac{-1}{2}(x - 9) & = y - 10 \\
-x + 9 & = 2y - 20 \\
-x + 29 & = 2y
\end{align*}
Now we have two equations with two unknowns. We can equate the two equations and solve for \(x\):
\begin{align*}
4x + 14 & = -x + 29 \\
5x & = 15 \\
x & = 3
\end{align*}
Now we can solve for \(y\):
\begin{align*}
2x + 7 & = y \\
2(3) + 7 & = y \\
13 & = y
\end{align*}
Therefore the coordinates of \(D\) are \((3;13)\).
Find the equation of a line parallel to the line \(BC\), which passes through the point \(A\).
We know from the first question that the gradient of line \(BC\) is 2. We also know that point \(A\)
is at \((-3;1)\).
The line parallel to \(BC\) will have the same gradient as \(BC\) so we can write the equation of
this line as: \(y = 2x + c\).
Now we can use point \(A\) to find the \(y\)-intercept of the line:
\begin{align*}
2 & = 2(-5) + c \\
2 & = -10 + c \\
12 & = c
\end{align*}
Therefore the equation of the line parallel to \(BC\) and passing through \(A\) is \(y = 2x + 12\).