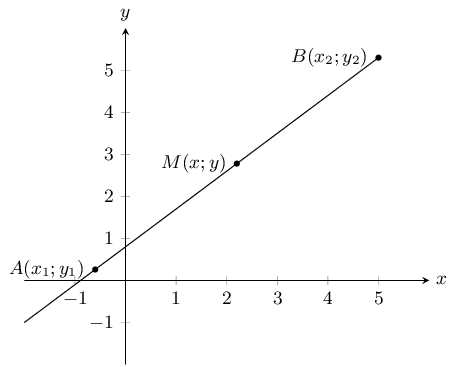
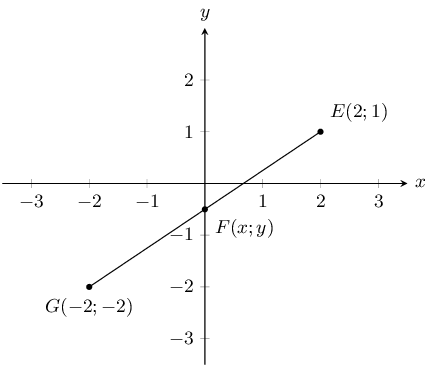
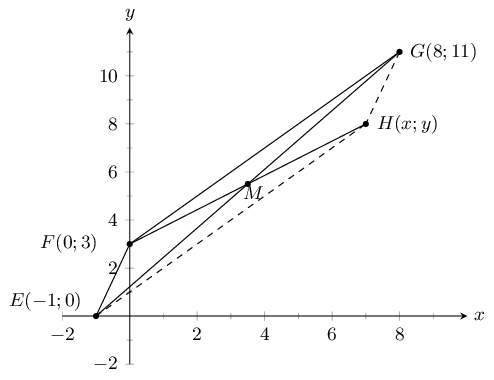
You are given the following diagram:
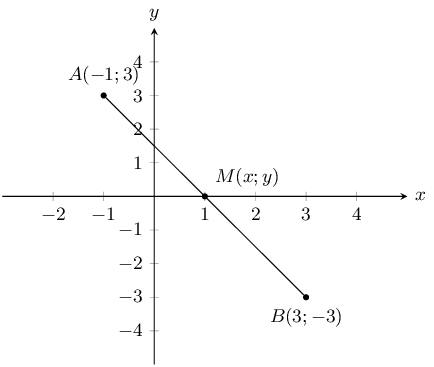
Calculate the coordinates of the mid-point (\(M\)) between point \(A
(-\text{1};\text{3})\) and point \(B (\text{3};-\text{3})\).
Let the coordinates of \(A\) be \(\left({x}_{1};{y}_{1}\right)\) and the
coordinates of \(B\) be \(\left({x}_{2};{y}_{2}\right)\).
\[{x}_{1} = -1 \quad {y}_{1} = 3 \quad {x}_{2} = 3 \quad {y}_{2} = -3\]
Substitute values into the mid-point formula:
\begin{align*}
M\left(x;y\right) & = \left(\frac{{x}_{1} + {x}_{2}}{2};\frac{{y}_{1} +
{y}_{2}}{2}\right) \\
x & = \frac{{x}_{1} + {x}_{2}}{2} \\
& = \frac{-1 + 3}{2} \\
& = 1 \\
y & = \frac{{y}_{1} + {y}_{2}}{2} \\
& = \frac{3 + (-3)}{2} \\
& = 0
\end{align*}
The mid-point is at \(M\left(1;0\right)\).
You are given the following diagram:

Calculate the coordinates of the mid-point (\(M\)) between point \(A
(-\text{2};\text{1})\) and point \(B (\text{1};-\text{3,5})\).
Let the coordinates of \(A\) be \(\left({x}_{1};{y}_{1}\right)\) and the
coordinates of \(B\) be \(\left({x}_{2};{y}_{2}\right)\).
\[{x}_{1} = -2 \quad {y}_{1} = 1 \quad {x}_{2} = 1 \quad {y}_{2} = -\text{3,5}\]
Substitute values into the mid-point formula:
\begin{align*}
M\left(x;y\right) & = \left(\frac{{x}_{1} + {x}_{2}}{2};\frac{{y}_{1} +
{y}_{2}}{2}\right) \\
x & = \frac{{x}_{1} + {x}_{2}}{2} \\
& = \frac{-2 + 1}{2} \\
& = -\text{0,5} \\
y & = \frac{{y}_{1} + {y}_{2}}{2} \\
& = \frac{1 + (-\text{3,5})}{2} \\
& = -\text{1,25}
\end{align*}
The mid-point is at \(M\left(-\text{0,5};-\text{1,25}\right)\).
\begin{align*}
M_{AB} &= \left(\frac{x_1 + x_2}{2};\frac{y_1 + y_2}{2}\right) \\
&= \left(\frac{2 - 4}{2};\frac{5 + 7}{2}\right) \\
&= \left(\frac{-2}{2};\frac{12}{2}\right) \\
&= (-1;6)
\end{align*}
\begin{align*}
M_{CD} &= \left(\frac{x_1 + x_2}{2};\frac{y_1 + y_2}{2}\right) \\
&= \left(\frac{5 + 23}{2};\frac{9 + 55}{2}\right) \\
&= \left(\frac{28}{2};\frac{64}{2}\right) \\
&= (14;32)
\end{align*}
\(E(x + 2;y - 1)\), \(F(x - 5;y - 4)\)
\begin{align*}
M_{EF} &= \left(\frac{x_1 + x_2}{2};\frac{y_1 + y_2}{2}\right) \\
&= \left(\frac{x + 2 + x - 5}{2};\frac{y - 1 + y - 4}{2}\right) \\
&= \left(\frac{2x - 3}{2};\frac{2y - 5}{2}\right)
\end{align*}
The mid-point \(M\) of \(PQ\) is \((3;9)\). Find \(P\) if \(Q\) is \((-2;5)\).
The mid-point formula is:
\[M\left(x;y\right) = \left(\frac{{x}_{1} + {x}_{2}}{2};\frac{{y}_{1} +
{y}_{2}}{2}\right)\]
Substituting values and solving for \({x}_{2}\) and \({y}_{2}\) gives:
\[\begin{array}{rlcrl}
3 & = \dfrac{-2 + {x}_{2}}{2} & \qquad\qquad & 9 & = \dfrac{5 +
{y}_{2}}{2} \\
6 & = -2 + {x}_{2} & \qquad\qquad & 18 & = 5 + {y}_{2} \\
{x}_{2} & = 6 + 2 & \qquad\qquad & {y}_{2} & = 18 - 5 \\
{x}_{2} & = 8 & \qquad\qquad & {y}_{2} & = 13
\end{array}\]
The coordinates of point \(P\) are \(\left(8;13\right)\).
\(PQRS\) is a parallelogram with the points \(P(5;3)\), \(Q(2;1)\) and
\(R(7;-3)\). Find point \(S\).
Draw a sketch:

The diagonals of a parallelogram bisect each other, therefore the mid-point of
\(QR\) will be the same as the mid-point of \(PS\). We must first find the
mid-point of \(QR\). We can then use it to determine the coordinates of point
\(H\).
\begin{align*}
M_{QR} &= \left(\frac{x_1 + x_2}{2};\frac{y_1 + y_2}{2}\right)\\
&= \left(\frac{2 + 7}{2};\frac{1 - 3}{2}\right) \\
&= \left(\frac{9}{2};\frac{-2}{2}\right) \\
&= \left(\frac{9}{2};-1\right)
\end{align*}
Use mid-point \(M\) to find the coordinates of \(S\):
\begin{align*}
M_{QR} &= (\frac{x_1 + x_2}{2};\frac{y_1 + y_2}{2}) \\
\left(\frac{9}{2};-1\right) &= \left(\frac{x + 5}{2};\frac{y + 3}{2}\right)
\end{align*}
Solve for \(x\):
\begin{align*}
\frac{9}{2} &= \frac{x + 5}{2} \\
9 &= x + 5 \\
x &= 4
\end{align*}
Solve for \(y\):
\begin{align*}
-1 &= \frac{y + 3}{2} \\
-2 &= y + 3 \\
y &= -5
\end{align*}
Therefore \(S(4;-5)\).