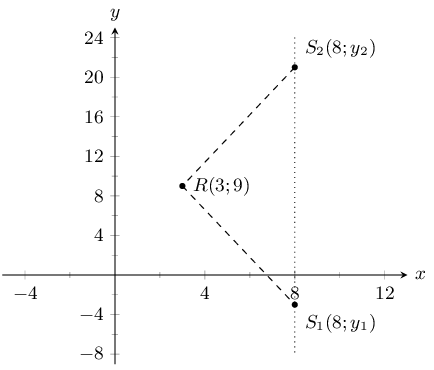
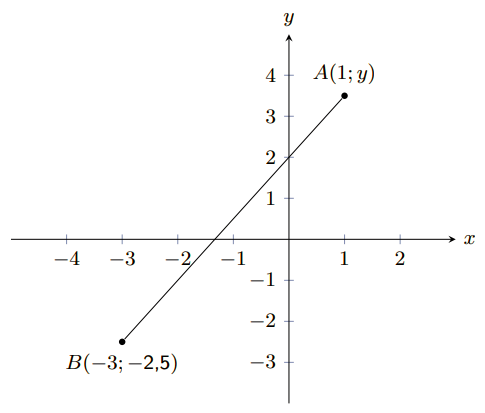You are given the following diagram:
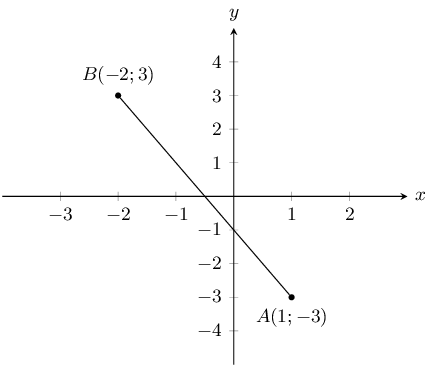
Calculate the length of line \(AB\), correct to 2 decimal places.
First we recall the equation for distance:
\(\begin{aligned}
d_{AB} & = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}\\
& = \sqrt{(\text{1} - (-\text{2}))^2 + (-\text{3} - (\text{3}))^2} \\
& = \sqrt{(\text{1} \text{+2})^2 + (-\text{3} -\text{3})^2} \\
& = \sqrt{(\text{3})^2 + (-\text{6})^2} \\
& = \sqrt{\text{9} + \text{36}} \\
& = \sqrt{\text{45}} \\
& \approx \text{6,71}
\end{aligned}\)
You are given the following diagram:

Calculate the length of line \(AB\), correct to 2 decimal places.
First we recall the equation for distance:
\(\begin{aligned}
d_{AB} & = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}\\
& = \sqrt{(\text{1} - (-\text{1}))^2 + (\text{1} - (\text{2}))^2} \\
& = \sqrt{(\text{1} \text{+1})^2 + (\text{1} -\text{2})^2} \\
& = \sqrt{(\text{2})^2 + (-\text{1})^2} \\
& = \sqrt{\text{4} + \text{1}} \\
& = \sqrt{\text{5}} \\
& \approx \text{2,24}
\end{aligned}\)
The following picture shows two points on the Cartesian plane, \(A\) and \(B\).
The distance between the points is \(\text{3,6056}\). Calculate the missing coordinate of point \(B\).
First we recall the equation for distance:
\(\begin{aligned}
d_{AB} & = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}\\
\text{3,6056} & = \sqrt{(x - (-\text{1}))^2 + (\text{0,5} - (\text{3,5}))^2} \\
\text{3,6056} & = \sqrt{(x \text{+1})^2 + (\text{0,5} -\text{3,5})^2}
\end{aligned}\)
Now we re-arrange, and solve for the value of \(x\):
\(\begin{aligned}
(\text{3,6056})^2 & = (x + \text{1})^2 + (\text{0,5} - \text{3,5})^2 \\
\text{13} & = (x + \text{1})^2 + (\text{0,5} -\text{3,5})^2 \\
\text{13} & = (x + \text{1})^2 + \text{9} \\
(x+1)^2 & = \text{4} \\
x + \text{1} & = \pm \sqrt{\text{4}} \\
x & = \pm \text{2} -\text{1} \\
x & = \text{1} \text{ or } -\text{3}
\end{aligned}\)
We now have a choice between 2 values for \(x\). From the diagram we can see that the appropriate value
for this question is \(x = \text{1}\).
Note that in this case we can use the diagram to check that our answer is valid but we can also calculate
the distance of line \(AB\) using our answer.
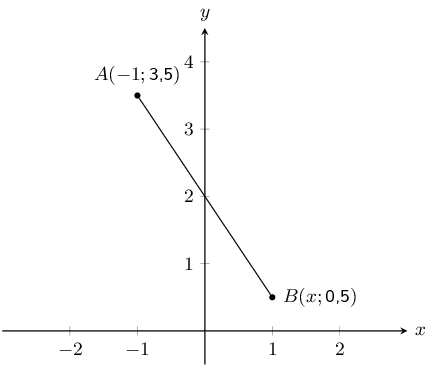
The following picture shows two points on the Cartesian plane, \(A\) and \(B\).
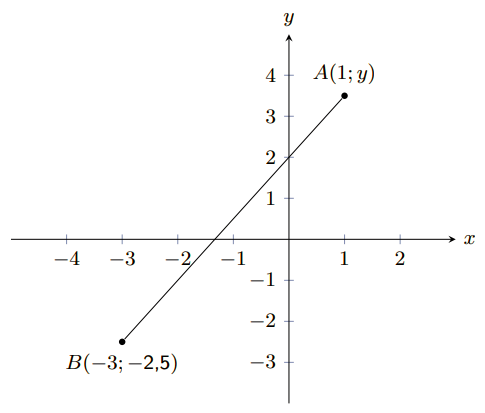
The line \(AB\) has a length of \(\text{7,2111}\). Calculate the missing coordinate of point \(B\). Round
your answer to one decimal place.
First we recall the equation for distance:
\(\begin{aligned}
d_{AB} & = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}\\
\text{7,2111} & = \sqrt{(\text{1} - (-\text{3}))^2 + (y - (-\text{2,5}))^2} \\
\text{7,2111} & = \sqrt{(\text{1} + \text{3})^2 + (y + \text{2,5})^2}
\end{aligned}\)
Now we re-arrange, and solve for the value of \(y\):
\(\begin{aligned}
(\text{7,2111})^2 & = (\text{1} + \text{3})^2 + (y + \text{2,5})^2 \\
\text{52} & = (\text{1} + \text{3})^2 + (y + \text{2,5})^2 \\
\text{52} & = (y + \text{2,5})^2 + \text{16} \\
(y + \text{2,5})^2 & = \text{36} \\
y + \text{2,5} & = \pm \sqrt{\text{36}} \\
y & = \pm \text{6} - \text{2,5} \\
y & = \text{3,5} \text{ or } -\text{8,5}
\end{aligned}\)
We now have a choice between 2 values for \(y\). From the diagram we can see that the appropriate value
for this question is \(y = \text{3,5}\).
Note that in this case we can use the diagram to check that our answer is valid but we can also calculate
the distance of line \(AB\) using our answer.
\(A(2;7)\) and \(B(-3;5)\)
\begin{align*}
d_{AB} &= \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\
& = \sqrt{(2 - (-3))^2 + (7 - 5)^2}\\
&= \sqrt{(5)^2 + (2)^2}\\
& = \sqrt{29}
\end{align*}
\(A(-3;5)\) and \(B(-9;1)\)
\begin{align*}
d_{AB} &= \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\
& = \sqrt{(-3 - (-9))^2 + (5 - 1)^2}\\
& = \sqrt{(6)^2 + (4)^2}\\
& = \sqrt{52}
\end{align*}
\(A(x;y)\) and \(B(x + 4; y - 1)\)
\begin{align*}
d_{AB} &= \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\
& = \sqrt{(x - (x + 4))^2 + (y - (y - 1))^2}\\
& = \sqrt{(x - x - 4)^2 + (y - y + 1)^2}\\
& = \sqrt{(-4)^2 + (1)^2}\\
& = \sqrt{17}
\end{align*}
If the distance between \(C(0;-3)\) and \(F(8;p)\) is 10 units, find the possible values of \(p\).
\begin{align*}
10 & = \sqrt{(8 - 0)^{2} + (p + 3)^{2}} \\
& = \sqrt{8^{2} + (p + 3)^{2}} \\
100 & = 8^{2} + (p + 3)^{2} \\
36 & = p^{2} + 6p + 9 \\
0 & = p^{2} + 6p - 27 \\
& = (p - 3)(p + 9) \\
\therefore p = 3 & \text{ or } p = -9
\end{align*}
Check \(p = 3\):
\begin{align*}
d & = \sqrt{{\left({x}_{1} - {x}_{2}\right)}^{2} + {\left({y}_{1} - {y}_{2}\right)}^{2}} \\
& = \sqrt{{\left(8 - 0\right)}^{2} + {\left(3 + 3\right)}^{2}} \\
& = \sqrt{64 + 36} \\
& = \sqrt{100} \\
& = 10
\end{align*}
Solution is valid.
Check \(p = -9\):
\begin{align*}
d & = \sqrt{{\left({x}_{1} - {x}_{2}\right)}^{2} + {\left({y}_{1} - {y}_{2}\right)}^{2}} \\
& = \sqrt{{\left(8 - 0\right)}^{2} + {\left(-9 + 3\right)}^{2}} \\
& = \sqrt{64 + 36} \\
& = \sqrt{100} \\
& = 10
\end{align*}
Solution is valid.
Therefore \(p = 3\) or \(p = -9\).