22.3 Kinetic energy | Mechanical energy

22.3 Kinetic energy (ESAHL)

Kinetic energy

Kinetic energy is the energy an object has due to its motion.

Quantity: Kinetic energy ${E}_{K}$ Unit name: Joule Unit symbol: J

Kinetic energy is the energy an object has because of its motion. This means that any moving object has kinetic energy. Kinetic energy is defined as:

\[{E}_{K} = \frac{1}{2}m{v}^{2}\]

where ${E}_{K}$ is the kinetic energy (measured in joules, $\text{J}$)

$m =$ mass of the the object (measured in $\text{kg}$)

$v =$ velocity of the object (measured in $\text{m·s$^{-1}$}$).

Therefore the kinetic energy ${E}_{K}$ depends on the mass and velocity of an object. The faster it moves, and the more massive it is, the more kinetic energy it has. A truck of $\text{2 000}$ $\text{kg}$, moving at $\text{100}$ $\text{km·h$^{-1}$}$ will have more kinetic energy than a car of $\text{500}$ $\text{kg}$, also moving at $\text{100}$ $\text{km·h$^{-1}$}$.

You may sometimes see kinetic energy written as KE. This is simply another way to write kinetic energy. We will not use this form in this book, but you may see it written like this in other books.

Consider the $\text{1}$ $\text{kg}$ suitcase on the cupboard that was discussed earlier. When it is on the top of the cupboard, it will not have any kinetic energy because it is not moving:

\begin{align*} {E}_{K} & = \frac{1}{2}m{v}^{2} \\ & = \frac{1}{2}\left(\text{1}\text{ kg}\right){\left(\text{0}\text{ m·s$^{-1}$}\right)}^{2} = \text{0}\text{ J} \end{align*}

When the suitcase falls, its velocity increases (falls faster), until it reaches the ground with a maximum velocity. As its velocity velocity increases, it will gain kinetic energy. Its kinetic energy will increase until it is a maximum when the suitcase reaches the ground. If it has a velocity of $\text{6,26}$ $\text{m·s$^{-1}$}$ when it reaches the ground, its kinetic energy will be:

\begin{align*} {E}_{K} & = \frac{1}{2}m{v}^{2} \\ & = \frac{1}{2}\left(\text{1}\text{ kg}\right){\left(\text{6,26}\text{ m·s$^{-1}$}\right)}^{2} = \text{19,6}\text{ J} \end{align*}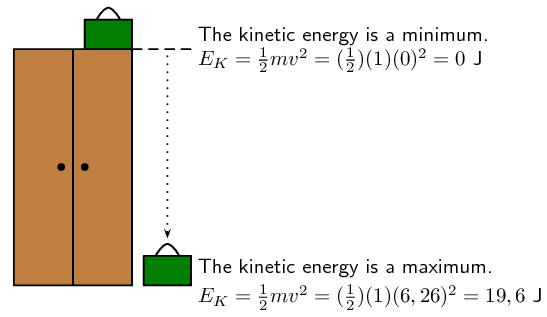

Worked example 3: Calculation of kinetic energy

A $\text{1}$ $\text{kg}$ brick falls off a $\text{4}$ $\text{m}$ high roof. It reaches the ground with a velocity of $\text{8,85}$ $\text{m·s$^{-1}$}$. What is the kinetic energy of the brick when it starts to fall and when it reaches the ground?

Analyse the question to determine what information is provided

The mass of the brick $m = \text{1}\text{ kg}$
The velocity of the brick at the bottom $v = \text{8,85}\text{ m·s$^{-1}$}$

These are both in the correct units so we do not have to worry about unit conversions.

Analyse the question to determine what is being asked

We are asked to find the kinetic energy of the brick at the top and the bottom. From the definition we know that to work out ${E}_{K}$, we need to know the mass and velocity of the object and we are given both of these values.

Calculate the kinetic energy at the top

Since the brick is not moving at the top, its kinetic energy is zero.

Substitute and calculate the kinetic energy

\begin{align*} {E}_{K} & = \frac{1}{2}m{v}^{2} \\ & = \frac{1}{2}\left(\text{1}\text{ kg}\right){\left(\text{8,85}\text{ m·s$^{-1}$}\right)}^{2} = \text{39,2}\text{ J} \end{align*}

Worked example 4: Kinetic energy of 2 moving objects

A herder is herding his sheep into the kraal. A mother sheep and its lamb are both running at $\text{2,7}$ $\text{m·s$^{-1}$}$ towards the kraal. The sheep has a mass of $\text{80}$ $\text{kg}$ and the lamb has a mass of $\text{25}$ $\text{kg}$. Calculate the kinetic energy for each of the sheep and the lamb.

Analyse the question to determine what information is provided

the mass of the mother sheep is $\text{80}$ $\text{kg}$
the mass of the lamb is $\text{25}$ $\text{kg}$
both the sheep and the lamb have a velocities of $\text{2,7}$ $\text{m·s$^{-1}$}$

Analyse the question to determine what is being asked

We need to find the kinetic energy of the sheep and the kinetic energy of its lamb

Use the definition to calculate the sheep's kinetic energy

\begin{align*} {E}_{K} & = \frac{1}{2}m{v}^{2} \\ & = \frac{1}{2}\left(\text{8}\text{ kg}\right){\left(\text{2,7}\text{ m·s$^{-1}$}\right)}^{2} = \text{291,6}\text{ J} \end{align*}

Use the definition to calculate the lamb's kinetic energy

\begin{align*} {E}_{K} & = \frac{1}{2}m{v}^{2} \\ & = \frac{1}{2}\left(\text{25}\text{ kg}\right){\left(\text{2,7}\text{ m·s$^{-1}$}\right)}^{2} = \text{91,13}\text{ J} \end{align*}

Note: Even though the sheep and the lamb are running at the same velocity, due to their different masses, they have different amounts of kinetic energy. The sheep has more than the lamb because it has a higher mass.

Checking units (ESAHM)

According to the equation for kinetic energy, the unit should be $\text{kg·m·s$^{-2}$}$. We can prove that this unit is equal to the joule, the unit for energy.

\begin{align*} \left(\text{kg}\right){\left(\text{m·s$^{-1}$}\right)}^{2} & = \left(\text{kg·m·s$^{-2}$}\right)·\text{m} \\ & = \text{N·m} \left(\text{ because Force }\left(\text{N}\right) = \text{ mass }\left(\text{kg}\right) \times \text{ acceleration }\left(\text{m·s$^{-2}$}\right)\right) \\ & = \text{J} \left(\text{ Work }\left(\text{J}\right) = \text{ Force }\left(\text{N}\right) \times \text{ distance }\left(\text{m}\right)\right) \end{align*}

We can do the same to prove that the unit for potential energy is equal to the joule:

\begin{align*} \left(\text{kg}\right)\left(\text{m·s$^{-2}$}\right)\left(\text{m}\right) & = \text{N·m} \\ & = \text{J} \end{align*}

Worked example 5: Mixing units and energy calculations

A bullet, having a mass of $\text{150}$ $\text{g}$, is shot with a muzzle velocity of $\text{960}$ $\text{m·s$^{-1}$}$. Calculate its kinetic energy.

Analyse the question to determine what information is provided

We are given the mass of the bullet m = $\text{150}$ $\text{g}$. This is not the unit we want mass to be in. We need to convert to $\text{kg}$.
\begin{align*} \text{Mass in grams } ÷ 1000 & = \text{ Mass in kg} \\ \text{150}\text{ g} ÷ 1000 & = \text{0,150}\text{ kg} \end{align*}
We are given the initial velocity with which the bullet leaves the barrel, called the muzzle velocity, and it is $v = \text{960}\text{ m·s$^{-1}$}$.

Analyse the question to determine what is being asked

We are asked to find the kinetic energy.

Substitute and calculate

We just substitute the mass and velocity (which are known) into the equation for kinetic energy:

\begin{align*} {E}_{K} & = \frac{1}{2}m{v}^{2} \\ & = \frac{1}{2}\left(\text{0,150}\text{ kg}\right){\left(\text{960}\text{ m·s$^{-1}$}\right)}^{2} \\ & = \text{69 120}\text{ J} \end{align*}

Kinetic energy

Textbook Exercise 22.2

Describe the relationship between an object's kinetic energy and its:

mass and
velocity

Solution not yet available

A stone with a mass of $\text{100}$ $\text{g}$ is thrown up into the air. It has an initial velocity of $\text{3}$ $\text{m·s$^{-1}$}$. Calculate its kinetic energy:

as it leaves the thrower's hand.
when it reaches its turning point.

Solution not yet available

A car with a mass of $\text{700}$ $\text{kg}$ is travelling at a constant velocity of $\text{100}$ $\text{km·hr$^{-1}$}$. Calculate the kinetic energy of the car.

Solution not yet available

22.2 Potential energy

Table of Contents

22.4 Mechanical energy