22.2 Potential energy | Mechanical energy

22.2 Potential energy (ESAHK)

The potential energy of an object is generally defined as the energy an object has because of its position relative to other objects that it interacts with. There are different kinds of potential energy such as gravitational potential energy, chemical potential energy, electrical potential energy, to name a few. In this section we will be looking at gravitational potential energy.

Potential energy: Potential energy is the energy an object has due to its position or state.

Gravitational potential energy

Gravitational potential energy is the energy an object has due to its position in a gravitational field relative to some reference point.

Quantity: Gravitational potential energy (${E}_{P}$) Unit name: Joule Unit symbol: J

In the case of Earth, gravitational potential energy is the energy of an object due to its position above the surface of the Earth. The symbol ${E}_{P}$ is used to refer to gravitational potential energy. You will often find that the words potential energy are used where gravitational potential energy is meant. We can define gravitational potential energy as:

\[{E}_{P}=mgh\]

where ${E}_{P} =$ potential energy (measured in joules, $\text{J}$)

$m =$ mass of the object (measured in $\text{kg}$)

$g =$ gravitational acceleration ($\text{9,8}$ $\text{m·s$^{-2}$}$)

$h =$ perpendicular height from the reference point (measured in $\text{m}$)

You may sometimes see potential energy written as PE. We will not use this notation in this book, but you may see it in other books.

You can treat the gravitational acceleration, $g$, as a constant and you will learn more about it in grade 11 and 12.

Let's look at the case of a suitcase, with a mass of $\text{1}$ $\text{kg}$, which is placed at the top of a $\text{2}$ $\text{m}$ high cupboard. By lifting the suitcase against the force of gravity, we give the suitcase potential energy. We can calculate its gravitational potential energy using the equation defined above as:

\begin{align*} {E}_{P} & = mgh \\ & = \left(\text{1}\text{ kg}\right)\left(\text{9,8}\text{ m·s$^{-2}$}\right)\left(\text{2}\text{ m}\right) = \text{19,6}\text{ J} \end{align*}

If the suitcase falls off the cupboard, it will lose its potential energy. Halfway down to the floor, the suitcase will have lost half its potential energy and will have only $\text{9,8}$ $\text{J}$ left.

\begin{align*} {E}_{P} & = mgh \\ & = \left(\text{1}\text{ kg}\right)\left(\text{9,8}\text{ m·s$^{-2}$}\right)\left(\text{1}\text{ m}\right) = \text{9,8}\text{ J} \end{align*}

At the bottom of the cupboard the suitcase will have lost all its potential energy and its potential energy will be equal to zero.

\begin{align*} {E}_{P} & = mgh \\ & = \left(\text{1}\text{ kg}\right)\left(\text{9,8}\text{ m·s$^{-2}$}\right)\left(\text{0}\text{ m}\right) = \text{0}\text{ J} \end{align*}

This example shows us that objects have maximum potential energy at a maximum height and will lose their potential energy as they fall.

Worked example 1: Gravitational potential energy

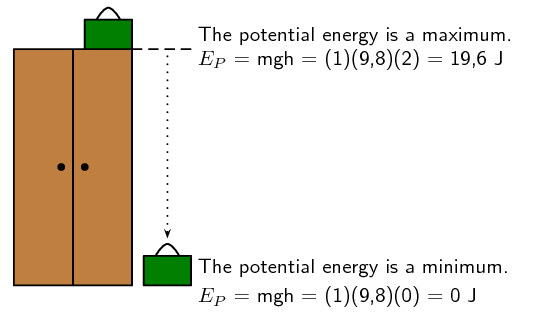
A brick with a mass of $\text{1}$ $\text{kg}$ is lifted to the top of a $\text{4}$ $\text{m}$ high roof. It slips off the roof and falls to the ground. Calculate the gravitational potential energy of the brick at the top of the roof and on the ground once it has fallen.

Analyse the question to determine what information is provided

The mass of the brick is $m = \text{1}\text{ kg}$
The height lifted is $h = \text{4}\text{ m}$

All quantities are in SI units.

Analyse the question to determine what is being asked

We are asked to find the gain in potential energy of the brick as it is lifted onto the roof.
We also need to calculate the potential energy once the brick is on the ground again.

Use the definition of gravitational potential energy to calculate the answer

\begin{align*} {E}_{P} & = mgh \\ & = \left(\text{1}\text{ kg}\right)\left(\text{9,8}\text{ m·s$^{-2}$}\right)\left(\text{4}\text{ m}\right) = \text{39,2}\text{ J} \end{align*}

Worked example 2: More gravitational potential energy

A netball player, who is $\text{1,7}$ $\text{m}$ tall, holds a $\text{0,5}$ $\text{kg}$ netball $\text{0,5}$ $\text{m}$ above her head and shoots for the goal net which is $\text{2,5}$ $\text{m}$ above the ground. What is the gravitational potential energy of the ball:

when she is about to shoot it into the net?
when it gets right into the net?
when it lands on the ground after the goal is scored?

Analyse the question to determine what information is provided

the netball net is $\text{2,5}$ $\text{m}$ above the ground
the girl has a height of $\text{1,7}$ $\text{m}$
the ball is $\text{0,5}$ $\text{m}$ above the girl's head when she shoots for goal
the mass of the ball is $\text{0,5}$ $\text{kg}$

Analyse the question to determine what is being asked

We need to find the gravitational potential energy of the netball at three different positions:

when it is above the girl's head as she starts to throw it into the net
when it reaches the net
when it reaches the ground

Use the definition of gravitational potential energy to calculate the value for the ball when the girl shoots for goal

\[{E}_{P}=mgh\]

First we need to calculate h. The height of the ball above the ground when the girl shoots for goal is h = ($\text{1,7}$ + $\text{0,5}$) = $\text{2,2}$ $\text{m}$.

Now we can use this information in the equation for gravitational potential energy:

\begin{align*} {E}_{P} & = mgh \\ & = \left(\text{0,5}\text{ kg}\right)\left(\text{9,8}\text{ m·s$^{-2}$}\right)\left(\text{2,2}\text{ m}\right) \\ & = \text{10,78}\text{ J} \end{align*}

Calculate the potential energy of the ball at the height of the net

Again we use the definition of gravitational potential energy to solve this:

\begin{align*} {E}_{P} & = mgh \\ & = \left(\text{0,5}\text{ kg}\right)\left(\text{9,8}\text{ m·s$^{-2}$}\right)\left(\text{2,5}\text{ m}\right) \\ & = \text{12,25}\text{ J} \end{align*}

Calculate the potential energy of the ball on the ground

\begin{align*} {E}_{P} & = mgh \\ & = \left(\text{0,5}\text{ kg}\right)\left(\text{9,8}\text{ m·s$^{-2}$}\right)\left(\text{0}\text{ m}\right) \\ & = \text{0}\text{ J} \end{align*}

Gravitational potential energy

Textbook Exercise 22.1

Describe the relationship between an object's gravitational potential energy and its:

mass and
height above a reference point.

Solution not yet available

A boy, of mass $\text{30}$ $\text{kg}$, climbs onto the roof of a garage. The roof is $\text{2,5}$ $\text{m}$ from the ground.

How much potential energy did the boy gain by climbing onto the roof?
The boy now jumps down. What is the potential energy of the boy when he is $\text{1}$ $\text{m}$ from the ground?
What is the potential energy of the boy when he lands on the ground?

Solution not yet available

A hiker, of mass $\text{70}$ $\text{kg}$, walks up a mountain, $\text{800}$ $\text{m}$ above sea level, to spend the night at the top in the first overnight hut. The second day she walks to the second overnight hut, $\text{500}$ $\text{m}$ above sea level. The third day she returns to her starting point, $\text{200}$ $\text{m}$ above sea level.

What is the potential energy of the hiker at the first hut (relative to sea level)?
How much potential energy has the hiker lost during the second day?
How much potential energy did the hiker have when she started her journey (relative to sea level)?
How much potential energy did the hiker have at the end of her journey when she reached her original starting position?

Solution not yet available

22.1 Introduction

Table of Contents

22.3 Kinetic energy