4.5 Solving problems
Knowing how to recognise patterns and describe them using mathematical equations and rules helps us solve different types of problems. In fact, one of the problem solving strategies is to look for a pattern.
Worked example 4.16: Solving problems with patterns
Tlotliso is picking pears. The following table shows how many pears she has picked in total after a certain number of minutes.
| Time (minutes) | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|
| Total number of pears picked | \(1\) | \(6\) | \(11\) | \(16\) |
- If the pattern continues, how many pears will Tlotliso have picked after \(5\) minutes?
- Give a formula for the number of pears she has picked (𝑝) after 𝑚 minutes.
- Determine how many pears Tlotliso would have picked after \(45\) minutes.
Determine whether there is a constant difference in the pattern.
Let’s look at the differences between the terms:
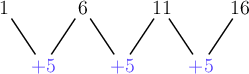
We can see that to get from one term to the next, we add \(5\) each time.
Determine the next term in the pattern.
To determine the number of pears picked after \(5\) minutes, we must add \(5\) to the value of the fourth term.
\[16 + 5 = 21\]Therefore, Tlotliso will have picked \(21\) pears after \(5\) minutes.
Identify the type of the pattern.
We know that the pattern has a constant difference of \(5\), so it is therefore a linear pattern.
Linear patterns always have a formula that includes the term number multiplied by the constant difference, as well as a constant term.
We know, therefore, that this pattern has the formula \(p = 5m + \square\). We still need to determine the value of the unknown constant term.
Determine the value of the constant term.
To determine the value of the constant term, we will look at the first term.
We know that the value of the first term is \(1\) (\(1\) pear was picked by the end of the first minute).
So we have:
\[\begin{align*} &1 = 5 \times 1 + \square \\ &1 = 5 + \square \end{align*}\]Therefore \(\square = - 4\) and the formula is \(p = 5m - 4\).
Substitute \(m = 45\) into the formula.
The formula tells us how many pears have been picked after any given number of minutes.
\[p = 5m - 4 = 5(45) - 4 = 221\]Therefore, Tlotliso would have picked \(221\) pears after \(45\) minutes.
