4.4 Describing patterns using rules and finding unknown terms
You have already seen that we can describe patterns in different ways. You have had a chance to discover how to investigate patterns, create rules, and find the unknown terms. We will now look at more examples and strategies.
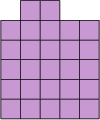
Look at the pattern below:
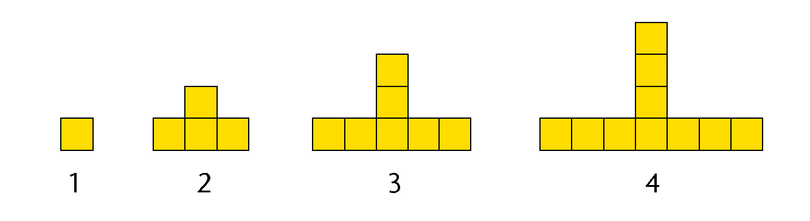
We can easily work out the number of squares that will be in picture \(5\):
- The bottom row of squares gets \(2\) more squares, \(1\) on each side.
- The vertical arrangement of squares gets \(1\) square on top.
- So, there must be \(13\) squares in picture \(5\).
It is easy to find the number of squares in the picture that follows a given diagrammatic arrangement. However, it will be more difficult to find the number of squares in picture \(20\) without knowing the rule.
Let’s try to organise the information in the table:
| Pattern number | Number of squares |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 7 |
| 4 | 10 |
| 5 | 13 |
| 6 | |
| … | … |
| 20 |
Looking at the numbers forming in the \(2\)nd row of the table, we can see that the sequence is growing by adding \(3\) to the previous term: \(1;4;7;10;13;\ldots\)
To find a way to get to term \(20\), or even better, to find the rule that does not depend on knowing the previous term, we need a plan…
Plan A
To get from \(1\) square to \(4\) squares, you have to add \(3\) squares. To get from \(4\) squares to \(7\) squares, you have to add \(3\) squares. To get from \(7\) squares to \(10\) squares, you have to add \(3\) squares. So continue to add \(3\) squares for each pattern until pattern \(20\).
Plan B
Multiply the position of the picture in a pattern by \(3\), and subtract \(2\). So, pattern \(\mathbf{20}\) will have \(\mathbf{20} \times 3 - 2\) squares.
If we use Plan B, then we can find the general rule. Let \(n\) be the position in a pattern, then the rule is: Number of squares \(= n \times 3 - 2\) squares or \(3n - 2\). Check that this works.
| Pattern number, n | Number of squares, 3n − 2 |
|---|---|
| 1 | 3(1) − 2 = 1 |
| 2 | 3(2) − 2 = 6 − 2 = 4 |
| 3 | 3(3) − 2 = 9 − 2 = 7 |
| 4 | 3(4) − 2 = 12 − 2 = 10 |
| 5 | 3(5) − 2 = 15 − 2 = 13 |
| 6 | 3(6) − 2 = 18 − 2 = 16 |
| … | … |
| 20 | 3(20) − 2 = 60 − 2 = 58 |
Worked example 4.14: Finding a formula to describe a pattern (linear)
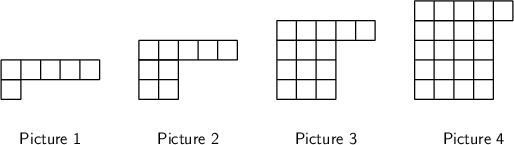
Consider the following pattern:
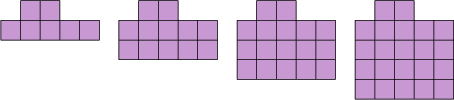
How many squares will there be in the fifth picture? Determine a formula for the number of squares (𝑠) that will be in the 𝑛th picture in the sequence (the formula for the general term). Hence, determine the number of squares needed to make the \(23\)rd picture.
Determine how each diagram is formed.
If we look at the pictures, we can see that five squares are added each time.
Determine the number of squares in the next picture.
We must continue this pattern to get the number of squares in the fifth picture:
\[22 + 5 = 27\]Therefore, the fifth picture will contain \(27\) squares.
Look for a pattern in the picture.

- The first picture has one row of five squares, plus two squares on top.
- The second picture has two rows of five squares, plus two squares on top.
- The third picture has three rows of five squares, plus two squares on top.
- And so on.
Find the rule.
Therefore, the 𝑛th picture will have 𝑛 rows of five squares, plus two squares on top. Algebraically, this is written as \(s = 5n + 2\).
Find the number of squares in the 23rd picture.
Substitute \(n = 23\) into the formula.
The formula gives us a rule to calculate the number of squares, given the picture number.
\[s = 5n + 2 = 5(23) + 2 = 117\]Therefore, there will be \(117\) squares in the \(23\)rd picture.
Worked example 4.15: Finding a formula to describe the pattern (quadratic)
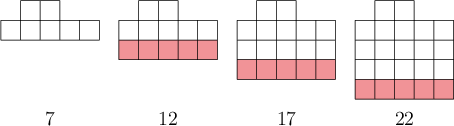
Consider the following pattern:
- How many squares will there be in the next picture?
- Give an expression or formula for the number of squares (𝑠) in the 𝑛th picture.
Notice the square part of each term.
One way to answer this question is to notice the perfect squares that form part of each picture. They are the square of \(1\) (\(1\)), then the square of \(2\) (\(4\)), and so on.
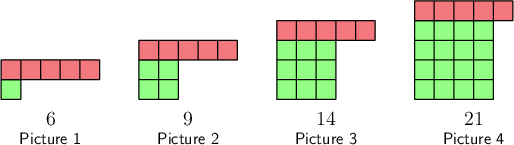
Find the number of squares in the next picture.
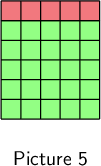
The number of squares in each picture is equal to its term number squared, plus five extra blocks on top. So the fifth picture will have \(5^{2} + 5 = 30\) squares.
You could also answer this question by looking at the pattern in the differences between the terms:
The differences increase by \(2\) each time. So, the next difference will be \(9\). \(21 + 9 = 30\), so this method also gives an answer of \(30\) squares.
Find the formula.
The number of squares in each picture is equal to its term number squared, plus five extra blocks on top.
The formula is therefore \(s = n^{2} + 5\).