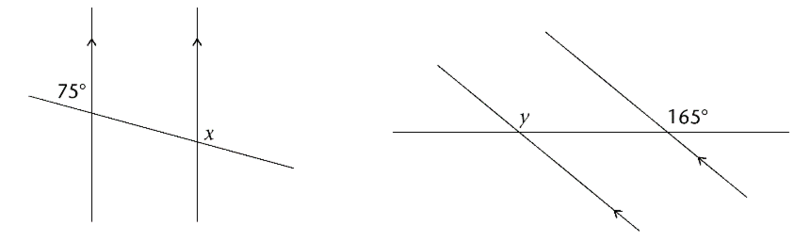
Calculate the size of \(x\) and \(y\).
|
Previous
Angles formed by lines intersected by a transversal
|
Next
Solving more geometric problems
|
Work out the sizes of the unknown angles, \(x\), \(y\) and \(z\). Give reasons for your answers.
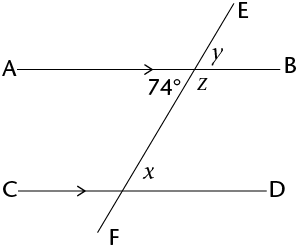
Remember that you can use abbreviations when you give your reasons within your workings. For example, for ‘alternate angles of parallel lines AB and CD are equal’ you write (alt \(\angle\)s ; \(AB \parallel CD\)).
Alternatively, we could have also solved the problem like this:
\[\begin{align} y &= 74^{\circ} && (\text{vert opp }\angle\text{s}) \\ x &= y &&(\text{corresp }\angle\; AB \parallel CD) \\ x &= 74^{\circ} \\ z +x &= 180^{\circ} &&(\text{co-int }\angle\; AB \parallel CD) \\ z +74^{\circ} &= 180 \\ z &= 180^{\circ}-74^{\circ} \\ z &= 106^{\circ} \end{align}\]Calculate the size of \(x\) and \(y\).

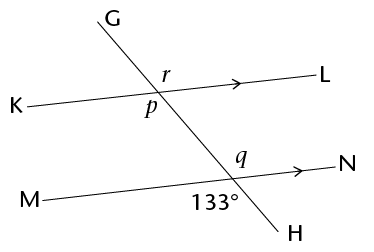
Calculate the size of \(p\), \(q\) and \(r\).
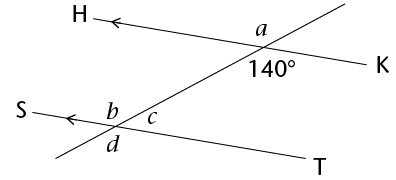
Calculate the size of \(a\), \(b\), \(c\) and \(d\).
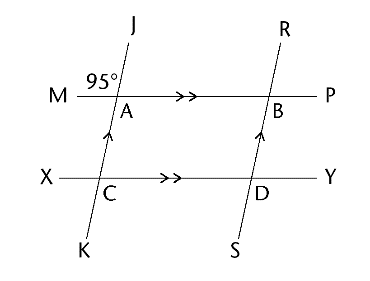
In the diagram, \(MP \parallel XY\) and \(JK \parallel RS\). Find the sizes of the marked angles.
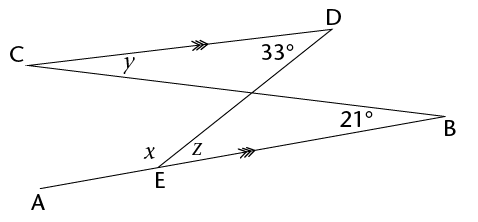
Calculate the size of \(x\), \(y\) and \(z\).
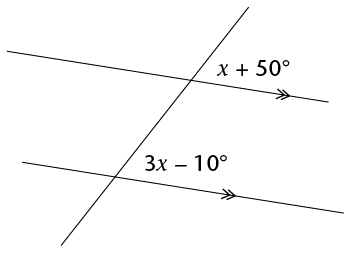
Calculate the size of \(x\).
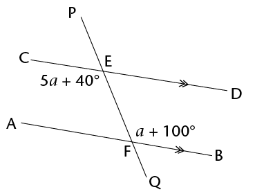
Calculate the size of \(a\) and \(C\hat{E}P\).
|
Previous
Angles formed by lines intersected by a transversal
|
Table of Contents |
Next
Solving more geometric problems
|