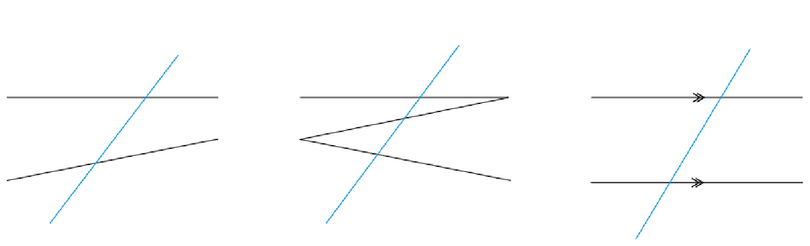
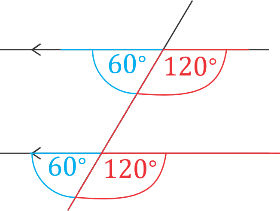
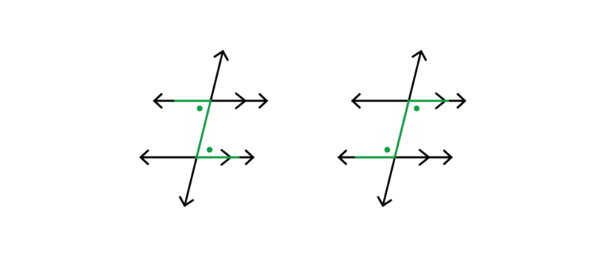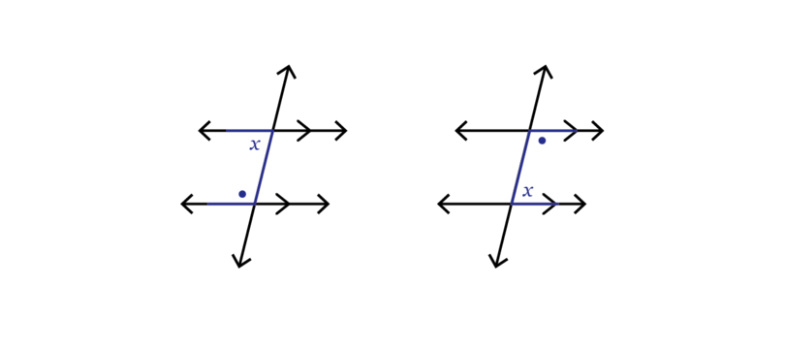A transversal is a line that crosses at least two other lines.
In the diagram below, the transversals (the blue lines) cut across the black lines.
- transversal
- a line that crosses at least two other lines
We will compare the three pairs of angles that are formed when a transversal intersects two lines. These pairs
are named by looking at their positions relative to the transversal:
- corresponding angles
- alternate angles
- co-interior angles.
Corresponding angles
The angles that lie on the same side of the transversal and are in matching positions are called
corresponding angles (corresp \(\angle\)s).
- corresponding angles
- angles that lie on the same side of the transversal and in matching positions
Exercise 12.3 Find corresponding angles
In the diagram, there are four pairs of corresponding angles. Find the corresponding angles.
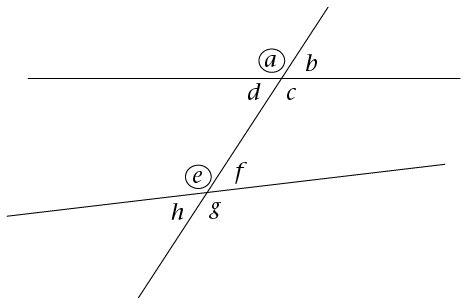
- \(a\) and \(e\) (they are both left of the transversal and above the lines)
- \(b\) and \(f\) (they are both right of the transversal and above the lines)
- \(d\) and \(h\) (they are both left of the transversal and below the lines)
- \(c\) and \(g\) (they are both right of the transversal and below the lines)
Alternate angles
Alternate angles (alt \(\angle\)s) lie on opposite (or alternate) sides of the transversal.
- alternate angles
- angles that lie on opposite (or alternate) sides of the transversal
Exercise 12.4 Find alternate angles
Find the alternate angles in the diagram.
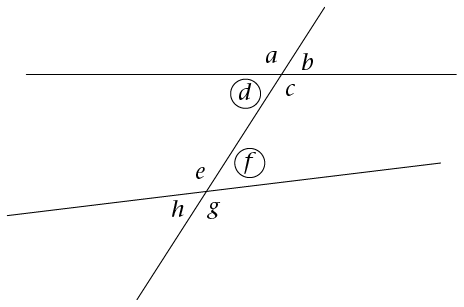
In the diagram, these are the alternate angles:
- \(d\) and \(f\) (they are on alternate sides of the transversal and lie on the inside of the
parallel lines)
- \(c\) and \(e\) (they are both on alternate sides of the transversal and lie on the inside of the
parallel lines).
Co-interior angles
Co-interior angles (co-int \(\angle\)s) lie on the same side of the transversal and between
the two lines.
- co-interior angles
- angles that lie on the same side of the transversal and on the inside of the two lines
Exercise 12.5 Find co-interior angles
Find the co-interior angles in the diagram.
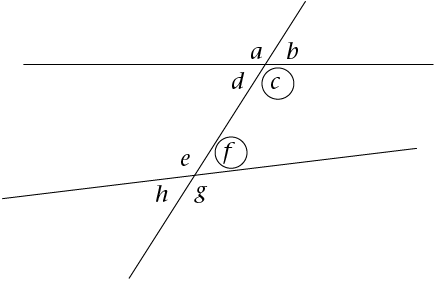
In the diagram, these are the co-interior angles:
- \(c\) and \(f\) (they are on the same side of the transversal and lie on the insides of both
parallel lines)
- \(d\) and \(e\) (they are on the same side of the transversal and lie on the insides of both
parallel lines).
Parallel lines intersected by a transversal
Two lines intersect if they cross each other at a point. For example, at a traffic intersection, two or more
streets intersect, and the middle of the intersection is the common point between the streets.
Parallel lines are two lines that are a constant distance apart. The symbol \(\parallel\) is
used to indicate parallel lines.
- parallel lines
- two lines that are a constant distance apart
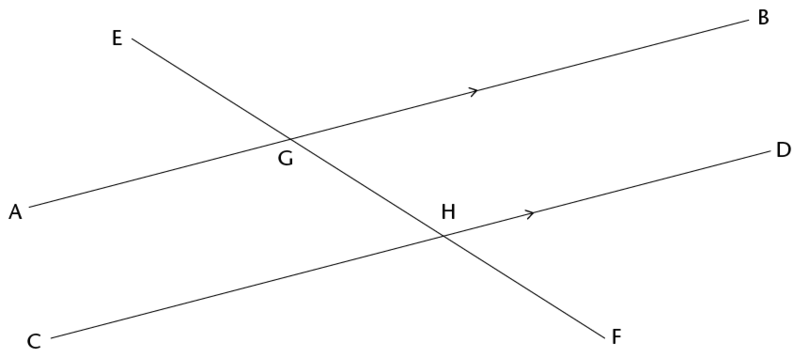
In this diagram, the lines AB and CD are parallel. We write: \(AB//CD\).
Parallel lines are indicated by arrow symbols, as shown in the diagram.
A transversal line intersects two or more lines. In the diagram above, the line EF cuts AB at G and CD at H. EF
is a transversal line.
When parallel lines are cut by a transversal:
- the corresponding angles are equal
- the alternate angles are equal
- the co-interior angles add up to \(180^{\circ}\).
Corresponding angles
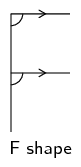
Look for angles forming an F pattern. Remember that corresponding angles are the angles in matching positions.
They are on the same side of the parallel lines, and on the same side of the transversal. The equal angles are
shown in the diagram.
If we colour the lines that make corresponding angles, we will see the F shape. This helps us to identify
corresponding angles.
Alternate angles
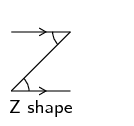
Look for angles forming a Z pattern. Remember that alternate angles are the angles that lie on alternate sides
of the transversal and inside the parallel lines. Alternate angles are equal.
If we colour the lines that make alternate angles, we will see a Z shape. This helps us identify alternate
angles.
Co-interior angles
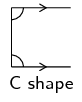
Look for angles forming a C pattern. These are angles that lie in between the parallel lines and on the same
side of the transversal. Co-interior angles are supplementary. This means that the sum of these two angles is
\(180^{\circ}\).
Hint: Be careful! These co-interior angles are not equal, but are supplementary.
If we colour the lines that make co-interior angles, we will see a C shape. This helps us identify co-interior
angles.
Remember that alternate angles and corresponding angles are equal, but only if the lines cut by the
transversal are parallel. Similarly, co-interior angles add up to \(180^\circ\), only if the lines cut
by the transversal are parallel.
Worked example 12.7: Identifying angles on
parallel lines
For the parallel lines intersected by a transversal shown in the diagrams below, identify:
- one pair of corresponding angles
- one pair of alternate angles
- one pair of co-interior angles
Similarly, the angle corresponding to \(120^{\circ}\) is shown in red. Notice that these angles form an F
pattern.
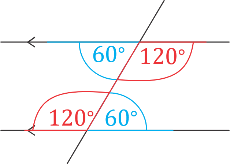
Similarly, the angle alternate to \(120^{\circ}\) is shown in red. Notice that the angles form a reflected
Z pattern on alternate sides of the transversal.
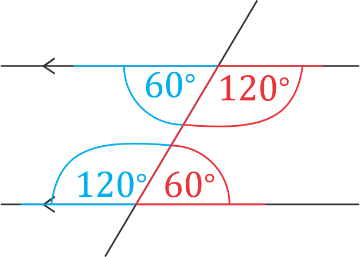
Similarly, the other pair of supplementary co-interior angles are shown in red. Notice that the angles
\(60^{\circ}\) and \(120^{\circ}\) form a C pattern on the same side of the transversal.