4.6 Summary
|
Previous
4.5 Applications of trigonometric functions
|
Next
End of chapter exercises
|
4.6 Summary (EMCGP)
|
Pythagorean Identities |
Ratio Identities |
|
\({\cos}^{2}\theta +{\sin}^{2}\theta =1\) |
\(\tan\theta =\frac{\sin\theta }{\cos\theta }\) |
|
\({\cos}^{2}\theta = 1 - {\sin}^{2}\theta\) |
\(\frac{\cos \theta}{\sin \theta} = \frac{1}{\tan \theta}\) |
|
\({\sin}^{2}\theta = 1 - {\cos}^{2}\theta\) |
Special angle triangles
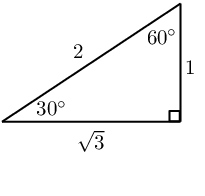
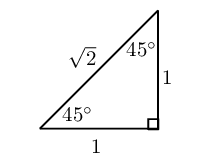
|
θ |
\(\text{0}\)° |
\(\text{30}\)° |
\(\text{45}\)° |
\(\text{60}\)° |
\(\text{90}\)° |
| \(\cos θ\) |
\(\text{1}\) |
\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{\sqrt{2}}\) |
\(\frac{1}{2}\) |
\(\text{0}\) |
| \(\sin θ\) |
\(\text{0}\) |
\(\frac{1}{2}\) |
\(\frac{1}{\sqrt{2}}\) |
\(\frac{\sqrt{3}}{2}\) |
\(\text{1}\) |
| \(\tan θ\) |
\(\text{0}\) |
\(\frac{1}{\sqrt{3}}\) |
\(\text{1}\) |
\(\sqrt{3}\) |
undef |
CAST diagram and reduction formulae

|
Negative angles |
Periodicity Identities |
Cofunction Identities |
|
\(\sin\left(-\theta \right)=-\sin\theta\) |
\(\sin\left(\theta ±{360}°\right)=\sin\theta\) |
\(\sin\left({90}°-\theta \right)=\cos\theta\) |
|
\(\cos\left(-\theta \right)=\cos\theta\) |
\(\cos\left(\theta ±{360}°\right)=\cos\theta\) |
\(\cos\left({90}°-\theta \right)=\sin\theta\) |
|
\(\tan\left(-\theta \right)=-\tan\theta\) |
\(\tan\left(\theta ±{180}°\right)=\tan\theta\) |
\(\sin\left({90}°+\theta \right)=\cos\theta\) |
|
\(\cos\left({90}°+\theta \right)=- \sin\theta\) |
|
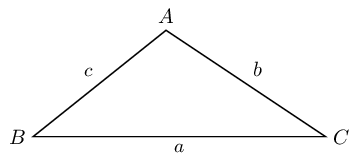
Area Rule |
Sine Rule |
Cosine Rule |
|
\(\text{Area}=\frac{1}{2}bc\sin \hat{A}\) |
\(\frac{\sin \hat{A}}{a}=\frac{\sin \hat{B}}{b}=\frac{\sin \hat{C}}{c}\) |
\({a}^{2}={b}^{2}+{c}^{2}-2bc\cos \hat{A}\) |
|
\(\text{Area}=\frac{1}{2}ab\sin \hat{C}\) |
\(a \sin \hat{B} = b \sin \hat{A}\) |
\({b}^{2}={a}^{2}+{c}^{2}-2ac\cos \hat{B}\) |
|
\(\text{Area}=\frac{1}{2}ac\sin \hat{B}\) |
\(b \sin{C} = c \sin \hat{B}\) |
\({c}^{2}={a}^{2}+{b}^{2}-2ab\cos \hat{C}\) |
|
\(a \sin{C} = c \sin \hat{A}\) |
|
Compound Angle Identities |
Double Angle Identities |
|
\(\sin\left(\theta +\beta\right)=\sin\theta\cos \beta +\cos\theta\sin \beta\) |
\(\sin\left(2\theta \right)=2\sin\theta\cos \theta\) |
|
\(\sin\left(\theta -\beta \right)=\sin\theta\cos \beta -\cos\theta\sin \beta\) |
\(\cos\left(2\theta \right)={\cos}^{2}\theta -{\sin}^{2}\theta\) |
|
\(\cos\left(\theta +\beta \right)=\cos\theta\cos \beta -\sin\theta\sin \beta\) |
\(\cos\left(2\theta \right)=1-2{\sin}^{2}\theta\) |
|
\(\cos\left(\theta -\beta \right)=\cos\theta\cos \beta +\sin\theta\sin \beta\) |
\(\cos\left(2\theta \right)=2{\cos}^{2}\theta - 1\) |
|
\(\) |
\(\tan\left(2\theta \right)=\frac{ \sin 2 \theta }{ \cos 2 \theta }\) |
|
Previous
4.5 Applications of trigonometric functions
|
Table of Contents |
Next
End of chapter exercises
|
