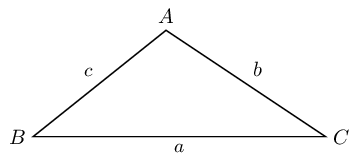
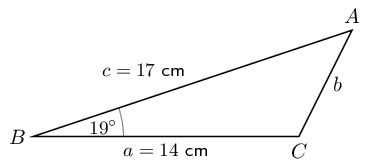
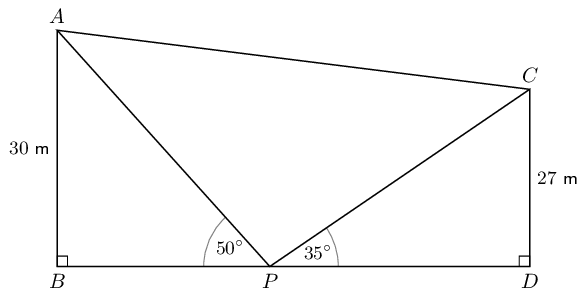
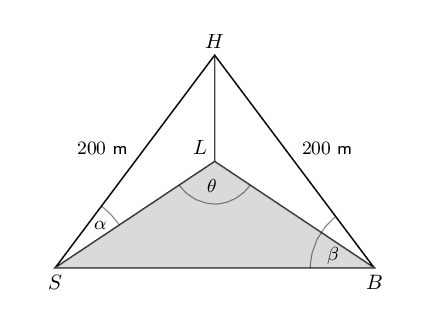
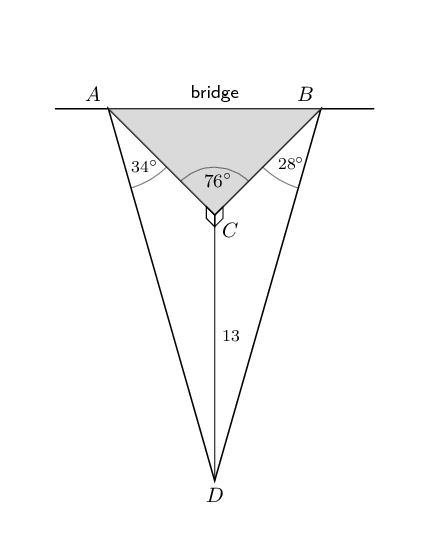
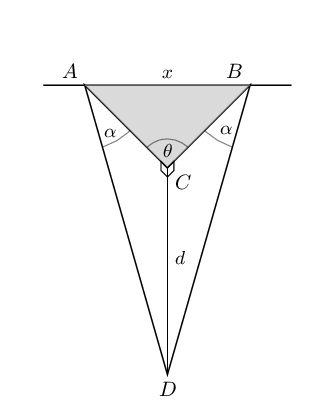
Determine the minimum length of cable needed to connect \(A\) and \(C\) (to the
nearest metre).
\begin{align*}
\hat{B} &= \hat{D} = \text{90} ° \quad (\text{vertical towers}) \\
& \\
\text{In } \triangle ABP: \quad \frac{30}{AP} &= \sin \text{50} ° \\
AP &= \frac{30}{\sin \text{50} °} \\
&= \text{39,16}\text{ m} \\
& \\
\text{In } \triangle CDP: \quad \frac{27}{CP} &= \sin \text{35} ° \\
CP &= \frac{27}{\sin \text{35} °} \\
&= \text{47,07}\text{ m} \\
& \\
\text{In } \triangle APC: A\hat{P}C &= \text{180} ° - ( \text{50} ° + \text{35} ° )
\\
&= \text{95} ° \\
AC^{2} &= AP^{2} + PC^{2} - 2(AP)(PC) \cos A\hat{P}C \\
&= (\text{39,16})^{2} + (\text{47,07})^{2} - 2(\text{39,16})(\text{47,07}) \cos \text{95} ° \\
&= \text{4 070,39} \\
\therefore AC &= \text{63,80}\text{ m} \\
&\approx \text{64}\text{ m}
\end{align*}
How far apart are the bases of the two towers (to the nearest metre)?
\begin{align*}
\text{In } \triangle ABP: \quad \frac{BP}{\text{39,16}} &= \cos \text{50} ° \\
\therefore BP &= \text{39,16} \cos \text{50} ° \\
&= \text{25,17}\text{ m} \\
& \\
\text{In } \triangle CDP: \quad \frac{PD}{\text{47,07}} &= \cos \text{35} ° \\
\therefore PD &= \text{47,07} \cos \text{35} ° \\
&= \text{38,56}\text{ m} \\
& \\
BD &= BP + PD \\\
&= \text{25,17}\text{ m} + \text{38,56}\text{ m} \\
&= \text{63,7}\text{ m} \\
&\approx \text{64}\text{ m}
\end{align*}