End of chapter exercises

Textbook Exercise 1.12

Is \(1+2+3+4+\cdots\) an example of a finite series or an infinite series?

Infinite arithmetic series

Calculate the total number of matches to be played in the competition.

\[7 + 6 + 5 + \ldots\] \begin{align*} a &= 7 \\ d &= -1 \\ S_{n} &= \frac{n}{2}[2a + (n-1)d] \\ S_{7} &= \frac{7}{2}[2(7) + (6)(-1)] \\ &= \frac{7}{2}[8] \\ &= 28 \end{align*} \(S_{7} = 28\)

If each of \(n\) teams played each other once, determine a formula for the total number of matches in terms of \(n\).

\[(n-1) + (n-2) + (n-3) + \ldots + 1\] \begin{align*} a &= n - 1 \\ d &= -1 \\ \l &= 1 \\ S_{n} &= \frac{n}{2}[a + \l] \\ S_{n-1} &= \frac{n-1}{2}[(n - 1) + (1)] \\ &= \frac{n-1}{2}[n] \\ &= \frac{n(n-1)}{2} \end{align*}

Calculate:

\[\sum _{k=2}^{6}3 {\left(\frac{1}{3}\right)}^{k+2}\]

Number of terms = end index - start index \(+ 1\) \(= (6 - 2) + 1 = 5\)

\begin{align*} k = 2: \quad T_{1} &= 3 \left( \frac{1}{3} \right)^{4} = \frac{1}{27} \\ k = 3: \quad T_{2} &= 3 \left( \frac{1}{3} \right)^{5} = \frac{1}{81} \\ \therefore r &= \frac{T_{2}}{T_{1}} = \frac{1}{3} \\ a &= \frac{1}{27} \\ \therefore S_{n} &= \frac{a(1 - r^{n})}{1 -r} \\ S_{5} &= \frac{\frac{1}{27}(1 - \left( \frac{1}{3} \right)^{5})}{1 - \frac{1}{3}} \\ &= \frac{\frac{1}{27}\left( \frac{242}{243} \right)}{\frac{2}{3}} \\ &= \frac{242}{6561} \times \frac{3}{2} \\ &= \frac{121}{2187} \end{align*}

Calculate the value of \(x\), (\(x \ne 1 \text{ or } 1\)).

\begin{align*} r &= \frac{T_{2}}{T_{1}} = \frac{T_{3}}{T_{2}}\\ \frac{x - 1}{x + 1} &= \frac{2x - 5}{x - 1} \\ \therefore (x - 1)^{2} &= (2x - 5)(x + 1) \\ x^{2} - 2x + 1 &= 2x^{2} - 3x - 5 \\ x^{2} - x - 6 &= 0 \\ (x - 3)(x + 2) &= 0 \\ \therefore x = 3 &\text{ or } x = -2 \\ \text{If } x &= -2 \\ \text{Geometric sequence: } & -1; -3; -9 \\ \therefore r &= 3 \\ \therefore & \text{ will diverge } \\ \text{If } x &= 3 \\ \text{Geometric sequence: } & 4; 2; 1 \\ \therefore r &= \frac{1}{2} \\ \therefore & \text{ will converge } \\ \therefore x &= 3 \end{align*}

Sum to infinity of the series.

\begin{align*} 4; \enspace 2; \enspace & 1; \ldots \\ S_{\infty} &= \frac{a}{1 -r} \\ &= \frac{4}{1 - \frac{1}{2}} \\ &= \frac{4}{\frac{1}{2}} \\ &= 8 \end{align*}

Write the sum of the first twenty terms of the following series in \(\sum\) notation.

\[6+3+\frac{3}{2}+\frac{3}{4}+\cdots\]

This is a geometric series:

\begin{align*} a &= 6 \\ r &= \frac{1}{2} \\ T_{n} &= ar^{n-1} \\ &= 6 \left( \frac{1}{2} \right)^{n-1} \\ \therefore & \sum_{n=1}^{20}{6\left( \frac{1}{2} \right)^{n-1} } \end{align*}

Determine:

\[\sum _{k=1}^{\infty }12{\left(\frac{1}{5}\right)}^{k-1}\]

\begin{align*} \sum _{k=1}^{\infty }12{\left(\frac{1}{5}\right)}^{k-1} & \\ \therefore & \text{ this is a geometric sequence } \\ r &= \frac{1}{5} \\ \therefore & \text{ series converges } \\ a &= 12 \\ S_{\infty} &= \frac{a}{1 - r} \\ &= \frac{12}{1 - \frac{1}{5}} \\ &= \frac{12}{ \frac{4}{5}} \\ &= 15 \end{align*}

What is the annual increase if he received a total of \(\text{R}\,\text{143 500}\) over \(\text{20}\) years?

\[4800 + (4800 + d) + (4800 + 2d) + \ldots\]

This is an arithmetic series.

\begin{align*} a &= \text{4 800} \\ S_{n} &= \frac{n}{2}[2a + (n - 1)d] \\ S_{20} &= \frac{20}{2}[2(\text{4 800}) + (20 - 1)d] \\ \text{And } S_{20} &= \text{143 500} \\ \therefore \text{143 500} &= 10 [\text{9 600} + 19d] \\ \text{14 350} &= \text{9 600} + 19d \\ \text{4 750} &= 19d \\ \therefore 250 &= d \end{align*}

His initial annual expenditure is \(\text{R}\,\text{2 600}\), which increases at a rate of \(\text{R}\,\text{400}\) per year. After how many years will his expenses exceed his income?

\[2600 + 3000 + 3400 + \ldots\]

This is an arithmetic series.

\begin{align*} a &= 2600 \\ d &= 400 \\ S_{n} &= \frac{n}{2}[2a + (n - 1)d] \\ S_{\text{expenses}} &= \frac{n}{2}[2(2600) + (n - 1)(400)] \\ S_{e} &= \frac{n}{2}[5200 + 400n - 400] \\ &= \frac{n}{2}[4800 + 400n] \end{align*} \begin{align*} S_{\text{income}} &= \frac{n}{2}[2(4800) + (n - 1)(250)] \\ S_{i} &= \frac{n}{2}[2(4800) + (n - 1)(250)] \\ &= \frac{n}{2}[9600 + 250n - 250] \\ &= \frac{n}{2}[9350 + 250n] \end{align*} \begin{align*} \text{let } S_{e} &= S_{i} \\ \frac{n}{2}[4800 + 400n] &= \frac{n}{2}[9350 + 250n] \\ 4800 + 400n &= 9350 + 250n \\ 150n &= 4550 \\ \therefore n &= \frac{4550}{150} \\ &= \text{30,333} \ldots \end{align*}

Therefore his expenses will exceed his income after \(\text{30}\) years.

The length of the side of a square is \(\text{4}\) units. This square is divided into \(\text{4}\) equal, smaller squares. One of the smaller squares is then divided into four equal, even smaller squares. One of the even smaller squares is divided into four, equal squares. This process is repeated indefinitely. Calculate the sum of the areas of the squares formed by this process of division.

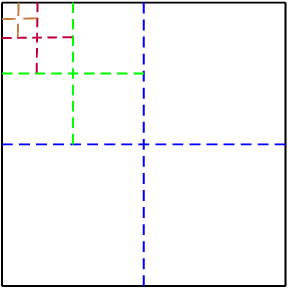
This gives the geometric series: \[16 + 4 + 1 + \frac{1}{4} + \ldots\]

\begin{align*} a &= 16 \\ r &= \frac{1}{4} \\ S_{\infty} &= \frac{a}{1 - r} \\ &= \frac{16}{1 - \frac{1}{4}} \\ &= \frac{16}{\frac{3}{4}} \\ &= \frac{64}{3} \end{align*}

Thembi worked part-time to buy a Mathematics book which costs \(\text{R}\,\text{29,50}\). On 1 February she saved \(\text{R}\,\text{1,60}\), and every day saves \(\text{30}\) \(\text{cents}\) more than she saved the previous day. So, on the second day, she saved \(\text{R}\,\text{1,90}\), and so on. After how many days did she have enough money to buy the book?

\[\text{1,60} + \text{1,90} + \text{2,10} + \ldots\]

This is an arithmetic series.

\begin{align*} a &= \text{1,60} \\ d &= \text{0,3} \\ S_{n} &= \frac{n}{2}[2a + (n-1)d] \\ \therefore \text{29,50} &= \frac{n}{2}[2(\text{1,60}) + (n-1)(\text{0,3})] \\ \text{59} &= n[\text{3,2} + \text{0,3}n - \text{0,3} ] \\ \text{59} &= \text{2,9}n + \text{0,3}n^{2} \\ (\times 10:) \quad 590 &= 29n + 3n^{2} \\ 0 &= 3n^{2} + 29n - 590 \\ 0 &= (3n + 59)(n - 10) \\ \therefore n = -\frac{59}{3} &\text{ or } n = 10 \\ \therefore n & = 10 \end{align*}

since \(n\) must be a positive integer.

A plant reaches a height of \(\text{118}\) \(\text{mm}\) after one year under ideal conditions in a greenhouse. During the next year, the height increases by \(\text{12}\) \(\text{mm}\). In each successive year, the height increases by \(\frac{5}{8}\) of the previous year's growth. Show that the plant will never reach a height of more than \(\text{150}\) \(\text{mm}\).

\[12 + 12 \left( \frac{5}{8} \right) + 12 \left( \frac{5}{8} \right)^{2} + \ldots 12 \left( \frac{5}{8} \right)^{n-1}\]

This is a geometric series.

\begin{align*} a &= 12 \\ r &= \frac{5}{8} \\ S_{\infty} &= \frac{a}{1 - r} \\ &= \frac{12}{1 - \frac{5}{8}} \\ &= \frac{12}{\frac{3}{8}} \\ &= 32 \end{align*}

Therefore the height of the plant is limited to \(\text{118}\) \(\text{mm}\) + \(\text{32}\) \(\text{mm}\) = \(\text{150}\) \(\text{mm}\)

Calculate the value of \(n\) if:

\[\sum_{a=1}^{n} \left(20-4a\right)=-20\]

\[16 + 12 + 8 + \ldots\]

This is an arithmetic series.

\begin{align*} a &= 16 \\ d &= -4 \\ S_{n} &= \frac{n}{2}[2a + (n-1)d] \\ -20 &= \frac{n}{2}[2(16) + (n-1)(-4)] \\ -40 &= n[32 - 4n + 4] \\ -40 &= 36n - 4n^{2} \\ 0 &= - 4n^{2} + 36n + 40 \\ &= n^{2} - 9n - 10 \\ &= (n + 1)(n - 10) \\ &= (n + 1)(n - 10) \\ \therefore n = -1 & \text{ or } n = 10 \\ \therefore n &= 10 \end{align*}

since \(n\) must be a positive integer.

How much did he save in the seventh working month?

\[400 + 400(\text{1,1}) + 400(\text{1,1})^{2} + \ldots\]

This is a geometric series.

\begin{align*} a &= 400 \\ r &= \text{1,1} \\ T_{n} &= ar^{n-1} \\ \therefore T_{7} &= 400(\text{1,1})^{6} \\ &= \text{708,62} \end{align*}

Therefore he saved \(\text{R}\,\text{708,62}\) in seventh month.

How much did he save all together in his first \(\text{12}\) working months?

\begin{align*} S_{12} &= \frac{a(1 - r^{n})}{1 - r} \\ &= \frac{400(1 - (\text{1,1})^{12})}{1 - \text{1,1}} \\ &= \text{8 553,71} \end{align*}

Therefore he saved \(\text{R}\,\text{8 553,71}\) in first \(\text{12}\) months.

The Cape Town High School wants to build a school hall and is busy with fundraising. Mr. Manuel, an ex-learner of the school and a successful politician, offers to donate money to the school. Having enjoyed mathematics at school, he decides to donate an amount of money on the following basis. He sets a mathematical quiz with \(\text{20}\) questions. For the correct answer to the first question (any learner may answer), the school will receive \(\text{R}\,\text{1}\), for a correct answer to the second question, the school will receive \(\text{R}\,\text{2}\), and so on. The donations \(1;2;4; \ldots\) form a geometric sequence. Calculate, to the nearest Rand:

The amount of money that the school will receive for the correct answer to the \(20^{\text{th}}\) question.

\[1 + 2 + 4 + \ldots\]

This is a geometric series.

\begin{align*} a &= 1 \\ r &= 2 \\ T_{n}&= ar^{n-1} \\ \therefore T_{20}&= (1) \left( 2^{19} \right) \\ &= \text{524 288} \end{align*}

They receive \(\text{R}\,\text{524 288}\) for question \(\text{20}\).

The total amount of money that the school will receive if all \(\text{20}\) questions are answered correctly.

\begin{align*} S_{n}&= \frac{a (r^{n} - 1)}{ r - 1} \\ &= \frac{(1)[2^{20} - 1]}{2 - 1} \\ &= \text{1 048 575} \end{align*}

They receive \(\text{R}\,\text{1 048 575}\)!

The first term of a geometric sequence is \(\text{9}\), and the ratio of the sum of the first eight terms to the sum of the first four terms is \(97:81\). Find the first three terms of the sequence, if it is given that all the terms are positive.

\begin{align*} S_{n} &= \frac{a(1 - r^{n})}{1 - r} \\ a &= 9 \\ \frac{S_{8}}{S_{4}} &= \frac{97}{81} \\ &= \frac{\frac{9(1 - r^{8})}{1 - r}}{\frac{9(1 - r^{4})}{1 - r}} \\ &= \frac{1 - r^{8}}{1 - r^{4}} \\ \therefore \frac{97}{81} &= \frac{1 - r^{8}}{1 - r^{4}} \\ \frac{97}{81} &= \frac{(1 - r^{4})(1 + r^{4})}{1 - r^{4}} \\ \frac{97}{81} &= 1 + r^{4} \\ \frac{16}{81} &= r^{4} \\ \therefore r &= \pm \frac{2}{3} \\ \text{But terms are positive } \therefore r &= \frac{2}{3} \end{align*} \[9; 6; 4; \ldots\]

Determine \(p\), (\(p \ne -\text{6} \text{ or } -\text{10}\)).

\begin{align*} \frac{10 + p}{6 + p} &= \frac{15 + p}{10 + p} \\ \therefore (10 + p)(10 + p) &= (15 + p)(6 + p) \\ 100 + 20p + p^{2} &= 90 + 21p + p^{2} \\ \therefore p &= 10 \end{align*}

Show that the constant ratio is \(\frac{5}{4}\).

\begin{align*} r &= \frac{10 + p}{6 + p} \\ &= \frac{20}{16} \\ &= \frac{5}{4} \end{align*}

Determine the tenth term of this sequence correct to one decimal place.

\begin{align*} T_{n} &= ar^{n-1} \\ T_{10} &= (16) \left( \frac{5}{4} \right)^{9} \\ &= \text{119,2} \end{align*} \(T_{10} = \text{119,2}\)

The second and fourth terms of a convergent geometric series are \(\text{36}\) and \(\text{16}\), respectively. Find the sum to infinity of this series, if all its terms are positive.

\begin{align*} \frac{T_{4}}{T_{2}} &= \frac{ar^{3}}{ar} \\ &= \frac{16}{36} \\ \therefore r^{2} &= \frac{16}{36} \\ r &= \pm \frac{2}{3} \\ \text{But terms are positive, } r &= \frac{2}{3} \\ T_{2} &= ar \\ &= 36 \end{align*} \begin{align*} a \left( \frac{2}{3} \right) &= 36 \\ \therefore a &= 54 \\ S_{\infty} &= \frac{a}{1 - r} \\ &= \frac{54}{1 - \frac{2}{3}} \\ &= 162 \end{align*}

Evaluate: \[\sum _{k=2}^{5}\frac{k\left(k+1\right)}{2}\]

\[\frac{2(2 + 1)}{2} + \frac{3(3 + 1)}{2} + \frac{4(4 + 1)}{2} + \frac{5(5 + 1)}{2}\] \[3 + 6 + 10 + 15 = 34\]

\({S}_{n}=4{n}^{2}+1\) represents the sum of the first \(n\) terms of a particular series. Find the second term.

\begin{align*} S_{n} &= 4{n}^{2}+1 \\ S_{1} &= 4{(1)}^{2}+1 = 5 \\ S_{2} &= 4{(2)}^{2}+1 = 17 \\ T_{2} &= S_{2} - S_{1} \\ &= 17 - 5 \\ &= 12 \end{align*}

\(x=-\frac{5}{2}\)

\begin{align*} x &= -\frac{5}{2} \\ \sum _{p=1}^{\infty }{\left(x+2\right)}^{p} &= \sum _{p=1}^{\infty }{\left( -\frac{5}{2}+2\right)}^{p} \\ &= \sum _{p=1}^{\infty }{\left( -\frac{1}{2}\right)}^{p} \end{align*} \[-\frac{1}{2}; \frac{1}{4}; -\frac{1}{8}; \ldots\]

This is a geometric sequence.

\begin{align*} r &= -\frac{1}{2} \\ \therefore & \text{ series converges since } \\ -1 & < r < 1 \\ S_{\infty} &= \frac{a}{1 - r} \\ &=\frac{-\frac{1}{2}}{1 - \left( -\frac{1}{2} \right)} \\ &= \frac{-\frac{1}{2}}{\frac{3}{2}} \\ &= -\frac{1}{3} \end{align*}

\(x=-5\)

\begin{align*} x &= -5 \\ \sum _{p=1}^{\infty }{\left(x+2\right)}^{p} &= \sum _{p=1}^{\infty }{\left( -5+2\right)}^{p} \\ &= \sum _{p=1}^{\infty }{\left( -3 \right)}^{p} \end{align*} \[-3; 9; -27; \ldots\]

This is a geometric sequence.

\begin{align*} r &= -3 \\ \therefore & \text{ series does not converge since } r < -1 \end{align*}

Calculate: \[\sum _{i=1}^{\infty } 5 \left( {4}^{-i} \right)\]

\[\frac{5}{4}; \frac{5}{4^{2}}; \frac{5}{4^{3}}; \ldots \frac{5}{4^{n}}\]

This is a geometric sequence.

\begin{align*} r &= \frac{1}{4} \\ a &= \frac{5}{4} \\ S_{\infty} &= \frac{a}{1 - r} \\ &= \frac{\frac{5}{4}}{1 - \frac{1}{4}}\\ &= \frac{5}{3} \end{align*}

The sum of the first \(p\) terms of a sequence is \(p \left(p+1\right)\). Find the tenth term.

\begin{align*} p=10: \quad S_{10} & = 10(10 + 1)= 110 \\ p=9: \quad S_{9} &= 9(9 + 1) = 90 \\ \text{And } T_{10} &= S_{10} - S_{9} \\ \therefore T_{10} &= 110 - 90 \\ &= 20 \end{align*}

Alternative method:

\begin{align*} p=1: \quad S_{1} &=a = 1(1 + 1)= 2 \\ p=2: \quad S_{2} &= 2(2 + 1) = 6 \\ \text{And } S_{2} &=T_{1} + T_{2} = 6 \\ \therefore T_{2} &= 6 - 2 = 4 \\ S_{3} &=T_{1} + T_{2} + T_{3}= 3 \times 4 = 12 \\ \therefore T_{3} &= 12 - 6 = 6 \end{align*} \[2; 4; 6; \ldots\]

This is an arithmetic sequence.

\begin{align*} a &= 2 \\ d &= 2 \\ T_{n} &= a + (n -1)d \\ T_{10} &= 2 + (10 -1)(2) \\ &= 20 \end{align*}

The powers of \(\text{2}\) are removed from the following set of positive integers

\(1; 2; 3; 4; 5; 6; \ldots;1998; 1999; 2000\)

Find the sum of remaining integers.

\[1; 2^{1}; 3; 2^{2}; 5; 6; \ldots 2000\] \begin{align*} S_{n} &= \frac{n}{2}[a + \l] \\ S_{2000} &= \frac{2000}{2}[1 + 2000]\\ &= 1000(2001) \\ &= 2001000 \end{align*}

Remove the powers of \(\text{2}\) to make a separate series:

\[2^{0}; 2^{1}; 2^{2}; \ldots 2^{10}\]

This is a geometric series.

\begin{align*} a &= 1 \\ r &= 2 \\ S_{n} &= \frac{a(r^{n} - 1)}{r - 1} \\ S_{11} &= \frac{1(2^{11} - 1)}{2 - 1} \\ &= 2047 \\ \therefore S_{2000} - S_{11} &= 2001000 - 2047 \\ &= 1998953 \end{align*}

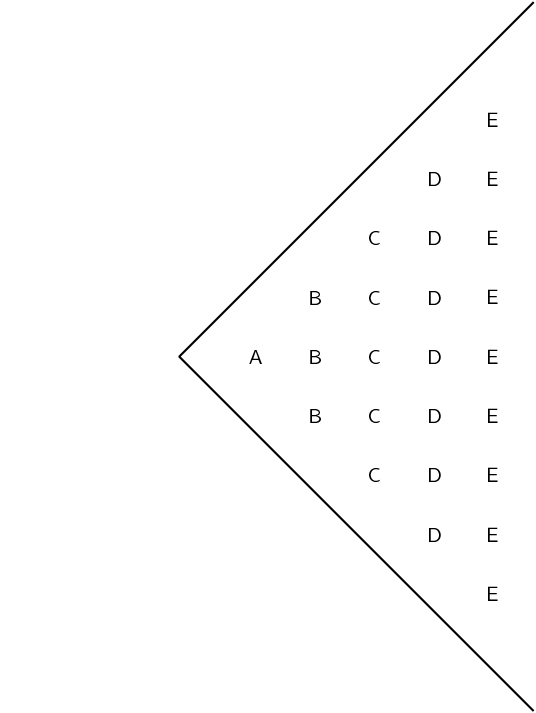
If the pattern continues, find the number of letters in the column containing M's.

\[1; 3; 5; 7; \ldots\]

This is an arithmetic series.

\begin{align*} a &= 1 \\ d &= 2 \\ T_{n} &= a + (n -1)d \\ \text{For the letter M: } \quad & n=13: \\ \quad T_{13} &= 1 + (12)(2) \\ &= 25 \end{align*}

If the total number of letters in the pattern is \(\text{361}\), which letter will be in the last column.

\begin{align*} S_{n} &= \frac{n}{2}[2a + (n - 1)d] \\ 361 &= \frac{n}{2}[2a + (n - 1)(2)] \\ 361 &= n[1 + n - 1] \\ 361 &= n^{2} \\ \therefore n &= \pm 19 \\ \therefore n &= 19 \end{align*}

so the letter “s” will be in the last column.

Write \(\text{0,5}\dot{\text{7}}\) as a proper fraction.

Rewrite the recurring decimal:

\begin{align*}\text{0,5}\dot{\text{7}} &= \text{0,5} + \text{0,0}\dot{\text{7}} \\ \text{0,5}\dot{\text{7}} &= \text{0,5} + [\text{0,07} + \text{0,007} + \ldots ] \end{align*}

The part in the square brackets is a geometric series with \(a = \frac{7}{100}\) and \(r = \frac{1}{10}\).

\begin{align*} S_{\infty} &= \frac{a}{1 -r} \\ &= \frac{\frac{7}{100}}{1 - \frac{1}{10}} \\ &= \frac{\frac{7}{100}}{ \frac{9}{10}} \\ &= \frac{7}{90} \\ \therefore \text{0,5}\dot{\text{7}} &= \text{0,5} + \text{0,0}\dot{\text{7}} \\ &= \frac{1}{2} + \frac{7}{90} \\ &= \frac{52}{90} \\ &= \frac{26}{45} \end{align*}

For which values of \(x\) will \(f(x)\) converge?

\[\frac{(1+x)}{1 - x} + \frac{(1+x)^{2}}{1 - x} + \frac{(1+x)^{3}}{1 - x} + \ldots\]

This is a geometric series with \(a = \frac{(1+x)}{1 - x}\) and \(r = (1 + x)\). For the series to converge:

\begin{align*} -1 &< r < 1 \\ -1 &< 1 + x < 1 \\ -2 &< x < 0 \end{align*}

Determine the value of \(f \left( -\frac{1}{2} \right)\).

\begin{align*} S_{\infty} &= \frac{a}{1 - r} \\ &= \frac{\frac{1+x}{1-x}}{1 - (1 + x)} \\ &= \frac{1 + x}{(1 - x)(-x)} \\ \text{Substitute } x&= -\frac{1}{2} \\ f(-\frac{1}{2})&= \frac{\frac{1}{2}}{\left(\frac{3}{2}\right) \left(\frac{1}{2}\right)} \\ &= \frac{2}{3} \end{align*}

From the definition of a geometric sequence, deduce a formula for calculating the sum of \(n\) terms of the series \[a^{2} + a^{4} + a^{6} + \cdots\]

\begin{align*} r &= a^{2} \\ T_{n} &= a^{2n} \\ \therefore S_{n} &= a^{2} + a^{4} + a^{6} + \ldots + a^{2n - 2} + a^{2n} \ldots \ldots (1) \\ r \times S_{n} = a^{2}S_{n} &= \qquad a^{4} + a^{6} + \ldots + a^{2n} + a^{2n + 2} \ldots \ldots (2) \\ (1) - (2): \quad S_{n} - a^{2}S_{n} &= a^{2} - a^{2n + 2} \\ S_{n}(1 - a^{2}) &= a^{2} - a^{2} \cdot a^{2n} \\ \therefore S_{n} &= \frac{a^{2}(1 - a^{2n})}{(1 - a^{2})} \end{align*}

Calculate the tenth term of the series if \(S_{n} = 2n + 3n^{2}\).

\begin{align*} p=10: \quad S_{10} &= 2(10) + 3(10)^{2} \\ & = 20 + 300 = 320 \\ p=9: \quad S_{9} &= 2(9) + 3(9)^{2} \\ &= 18 + 243 = 261 \\ \text{And } T_{10} &= S_{10} - S_{9} \\ \therefore T_{10} &= 320 - 261 \\ &= 59 \end{align*}

Alternative method:

\begin{align*} S_{1} &= T_{1} = 5 \\ S_{2} &= T_{1} + T_{2} = 16 \\ \therefore T_{2} &= 16 - 5 \\ &= 11 \\ S_{3} &= 2(3) + 3(3)^{2} = 33 \\ \therefore 33 &= T_{3} + S_{2} \\ \therefore T_{3} &= 17 \\ S_{n} &= 5 + 11 + 17 + \ldots \\ d &= 11 - 5 = 6 \\ d &= 17 - 11 = 6 \\ \therefore & \text{ this is an arithmetic series} \\ T_{10} &= a + (n-1)d \\ &= 5 + (9)(6) \\ &= 59 \end{align*}

A theatre is filling up at a rate of \(4\) people in the first minute, \(\text{6}\) people in the second minute, and \(\text{8}\) people in the third minute and so on. After \(\text{6}\) minutes the theatre is half full. After how many minutes will the theatre be full?

[IEB, Nov 2001]

\[4 + 6 + 8 + \ldots\] \begin{align*} d &= T_{2} - T_{1} \\ &= 6 - 4 \\ &= 2 \\ d &= T_{3} - T_{2} \\ &= 8 - 6 \\ &= 2 \\ \therefore & \text{ this is an arithmetic series} \\ S_{n} &= \frac{n}{2}[2a + (n-1)d] \\ S_{6} &= \frac{6}{2}[2(4) + (5)(2)] \\ &=3 (18) \\ &= 54 \quad \text{(theatre half full)}\\ \therefore 2 \times 54 &= 108 \quad \text{(theatre full)}\\ S_{n} &= \frac{n}{2}[2a + (n-1)d] \\ 108 &= \frac{n}{2}[2(4) + (n-1)(2)] \\ 216 &= n[8 + 2n - 2] \\ 0 &= 2n^{2} + 6n - 216 \\ 0 &= n^{2} + 3n - 108 \\ 0 &= (n + 12)(n - 9) \\ \therefore n = -12 &\text{ or } n = 9 \\ n & \text{ must be a positive integer } \\ \therefore n &= 9 \end{align*}

It takes \(\text{9}\) minutes for the theatre to be full.

1.7 Summary

Table of Contents

2.1 Revision