10.4 The fundamental counting principle | Probability

10.4 The fundamental counting principle (EMCJZ)

Mathematics began with counting. Initially, fingers, beans and buttons were used to help with counting, but these are only practical for small numbers. What happens when a large number of items must be counted?

This section focuses on how to use mathematical techniques to count different assortments of items.

Introduction (EMCK2)

An important aspect of probability theory is the ability to determine the total number of possible outcomes when multiple events are considered.

For example, what is the total number of possible outcomes when a die is rolled and then a coin is tossed? The roll of a die has six possible outcomes (\(1;2;3;4;5\) or \(\text{6}\)) and the toss of a coin, \(\text{2}\) outcomes (heads or tails). The sample space (total possible outcomes) can be represented as follows:

\[S = \left\{\begin{array}{cccccc} (1;H); & (2;H); & (3;H); & (4;H); & (5;H); & (6;H); \\ (1;T); & (2;T); & (3;T); & (4;T); & (5;T); & (6;T) \end{array}\right\}\]

Therefore there are \(\text{12}\) possible outcomes.

The use of lists, tables and tree diagrams is only feasible for events with a few outcomes. When the number of outcomes grows, it is not practical to list the different possibilities and the fundamental counting principle is used instead.

The fundamental counting principle: The fundamental counting principle states that if there are \(n(A)\) outcomes in event \(A\) and \(n(B)\) outcomes in event \(B\), then there are \(n(A) \times n(B)\) outcomes in event \(A\) and event \(B\) combined.

If we apply this principle to our previous example, we can easily calculate the number of possible outcomes by multiplying the number of possible die rolls with the number of outcomes of tossing a coin: \(6 \times 2 = 12\) outcomes. This allows us to formulate the following:

If there \(n_{1}\) possible outcomes for event \(A\) and \(n_{2}\) outcomes for event \(B\), then the total possible number of outcomes for both events is \(n_1 \times n_2\)

This can be generalised to \(k\) events, where \(k\) is the number of events. The total number of outcomes for \(k\) events is:

\[{n}_{1}\times {n}_{2}\times {n}_{3}\times \cdots \times {n}_{k}\]

The order in which the experiments are done does not affect the total number of possible outcomes.

Worked example 10: Choices without repetition

A take-away has a 4-piece lunch special which consists of a sandwich, soup, dessert and drink for R \(\text{25,00}\). They offer the following choices for:

Sandwich: chicken mayonnaise, cheese and tomato, tuna mayonnaise, ham and lettuce

Soup: tomato, chicken noodle, vegetable

Dessert: ice-cream, piece of cake

Drink: tea, coffee, Coke, Fanta, Sprite

How many possible meals are there?

Determine how many parts to the meal there are

There are 4 parts: sandwich, soup, dessert and drink.

Identify how many choices there are for each part

Meal component	Sandwich	Soup	Dessert	Drink
Number of choices	\(\text{4}\)	\(\text{3}\)	\(\text{2}\)	\(\text{5}\)

Use the fundamental counting principle to determine how many different meals are possible

\(4\times 3\times 2\times 5=120\)

So there are \(\text{120}\) possible meals.

temp text

In the previous example, there were a different number of options for each choice. But what happens when the number of choices is unchanged each time you choose?

For example, if a coin is flipped three times, what is the total number of different results? Each time a coin is flipped, there are two possible outcomes, namely heads or tails. The coin is flipped \(\text{3}\) times. We can use a tree diagram to determine the total number of possible outcomes:

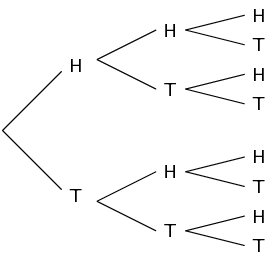
From the tree diagram, we can see that there is a total of 8 different possible outcomes.

Drawing a tree diagram is possible to draw for three different coin flips, but as soon as the number of events increases, the total number of possible outcomes increases to the point where drawing a tree diagram is impractical.

For example, think about what a tree diagram would look like if we were to flip a coin six times. In this case, using the fundamental counting principle is a far easier option. We know that each time a coin is flipped that there are two possible outcomes. So if we flip a coin six times, the total number of possible outcomes is equivalent to multiplying 2 by itself six times:

\[2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^{6} = 64\]

Another example is if you have the letters A, B, C, and D and you wish to discover the number of ways of arranging them in three-letter patterns if repetition is allowed, such as ABA, DCA, BBB etc. You will find that there are \(\text{64}\) ways. This is because for the first letter of the pattern, you can choose any of the four available letters, for the second letter of the pattern, you can choose any of the four letters, and for the final letter of the pattern you can choose any of the four letters. Multiplying the number of available choices for each letter in the pattern gives the total available arrangements of letters:

\[4 \times 4 \times 4 = 4^{3} = 64\]

This allows us to formulate the following:

When you have \(n\) objects to choose from and you choose from them \(r\) times, then the total number of possibilities is \[n \times n \times n \ldots \times n \enspace (r \text{ times}) = n^{r}\]

Worked example 11: Choices with repetition

A school plays a series of \(\text{6}\) soccer matches. For each match there are \(\text{3}\) possibilities: a win, a draw or a loss. How many possible results are there for the series?

Determine how many outcomes you have to choose from for each event

There are \(\text{3}\) outcomes for each match: win, draw or lose.

Determine the number of events

There are \(\text{6}\) matches, therefore the number of events is \(\text{6}\).

Determine the total number of possible outcomes

There are \(\text{3}\) possible outcomes for each of the \(\text{6}\) events. Therefore, the total number of possible outcomes for the series of matches is

\[3 \times 3 \times 3 \times 3 \times 3 \times 3 = 3^6 = 729\]

temp text

Number of possible outcomes if repetition is allowed

Textbook Exercise 10.4

Tarryn has five different skirts, four different tops and three pairs of shoes. Assuming that all the colours complement each other, how many different outfits can she put together?

\[5 \times 4 \times 3 = \text{60} \text{ different outfits}\]

In a multiple-choice question paper of \(\text{20}\) questions the answers can be A, B, C or D. How many different ways are there of answering the question paper?

\[4^{20} = \text{1,0995} \times \text{10}^{\text{12}} \text{ different ways of answering the exam paper}\]

A debit card requires a five digit personal identification number (PIN) consisting of digits from 0 to 9. The digits may be repeated. How many possible PINs are there?

\[10^{5} = \text{100 000} \text{ possible PINs}\]

The province of Gauteng ran out of unique number plates in 2010. Prior to 2010, the number plates were formulated using the style LLLDDDGP, where L is any letter of the alphabet excluding vowels and Q, and D is a digit between 0 and 9. The new style the Gauteng government introduced is LLDDLLGP. How many more possible number plates are there using the new style when compared to the old style?

\begin{align*} \text{Old style: } 20^{3} \times 10^{3} &= \text{8 000 000} \text{ possible arrangements} \\ \text{New style: } 20^{4} \times 10^{2} &= \text{16 000 000} \text{ possible arrangements} \\ \text{16 000 000} - \text{8 000 000} &= \text{8 000 000} \end{align*}

Therefore there are \(\text{8 000 000}\) more possible number plates using the new style.

A gift basket is made up from one CD, one book, one box of sweets, one packet of nuts and one bottle of fruit juice. The person who makes up the gift basket can choose from five different CDs, eight different books, three different boxes of sweets, four kinds of nuts and six flavours of fruit juice. How many different gift baskets can be produced?

\[5 \times 8 \times 3 \times 4 \times 6 = \text{2 880} \text{ possible gift baskets}\]

the digits and letters of the alphabet can be repeated.

\[10^{4} \times 26^{3} = \text{175 760 000} \text{ possible codes}\]

the digits and letters of the alphabet can be repeated, but the code may not contain a zero or any of the vowels in the alphabet.

We exclude the digit \(\text{0}\) and the vowels (A; E; I; O; U), leaving \(\text{9}\) other digits and \(\text{21}\) letters to choose from.

\[9^{4} \times 21^{3} = \text{60 761 421} \text{ possible codes}\]

the digits and letters of the alphabet can be repeated, but the digits may only be prime numbers and the letters X, Y and Z are excluded from the code.

The prime digits are \(\text{2}\), \(\text{3}\), \(\text{5}\) and \(\text{7}\). This gives us 4 possible digits. If we exclude the letters X, Y and Z, we are left with \(\text{23}\) letters to choose from.

\[4^{4} \times 23^{3} = \text{3 114 752} \text{ possible codes}\]

A restaurant offers four choices of starter, eight choices for the main meal and six choices for dessert. A customer can choose to eat just one course, two different courses or all three courses. Assuming that all courses are available, how many different meal options does the restaurant offer?

A person who eats only a starter has 4 choices
A person who eats only a main meal has 8 choices
A person who eats only a dessert has 6 choices
A person who eats a starter and a main course has \(4 \times 8 = 32\) choices
A person who eats a starter and a dessert has \(4 \times 6 = 24\) choices
A person who eats a main meal and a dessert has \(8 \times 6 = 48\) choices
A person who eats all three courses has \(4 \times 8 \times 6 = 192\) choices.

\[\text{Therefore, there are } 4 + 8 + 6 + 32 +24 + 48 + 192 = \text{314} \text{ different meal options}\]

10.3 Tools and Techniques

Table of Contents

10.5 Factorial notation