2.7 Summary
|
Previous
2.6 Exponential functions
|
Next
2.8 Enrichment: more on logarithms
|
2.7 Summary (EMCFQ)
-
Function: a rule which uniquely associates elements of one set \(A\) with the elements of another set \(B\); each element in set \(A\) maps to only one element in set \(B\).
-
Functions can be one-to-one relations or many-to-one relations. A many-to-one relation associates two or more values of the independent (input) variable with a single value of the dependent (output) variable.
-
Vertical line test: if it is possible to draw any vertical line which crosses the graph of the relation more than once, then the relation is not a function.
-
Given the invertible function \(f(x)\), we determine the inverse \(f^{-1}(x)\) by:
- replacing every \(x\) with \(y\) and \(y\) with \(x\);
- making \(y\) the subject of the equation;
- expressing the new equation in function notation.
-
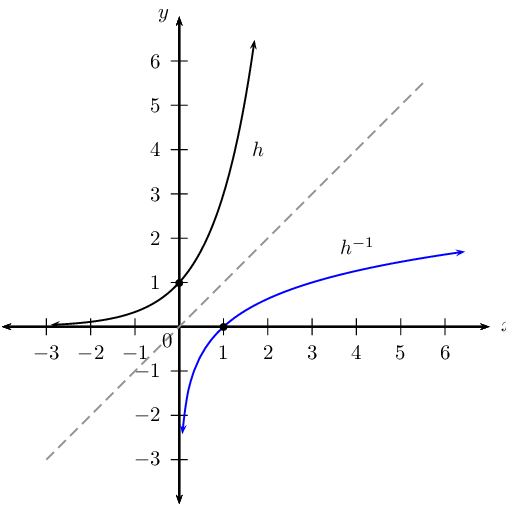
If we represent the function \(f\) and the inverse function \({f}^{-1}\) graphically, the two graphs are reflected about the line \(y=x\).
-
The domain of the function is equal to the range of the inverse. The range of the function is equal to the domain of the inverse.
-
The inverse function of a straight line is also a straight line. Vertical and horizontal lines are exceptions.
-
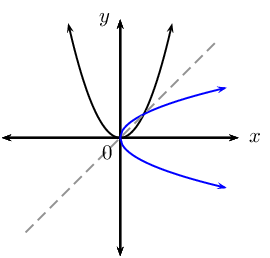
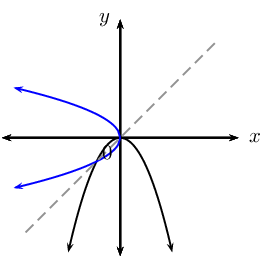
The inverse of a parabola is not a function. However, we can limit the domain of the parabola so that the inverse of the parabola is a function.
-
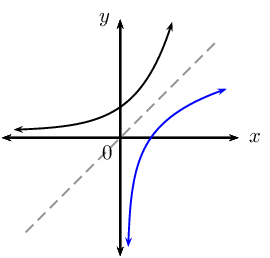
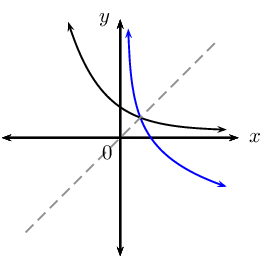
The inverse of the exponential function \(f(x) = b^{x}, (b > 0, b \ne 1)\) is the logarithmic function \(f^{-1}(x) = \log_{b}{x}\).
-
The “common logarithm” has a base \(\text{10}\) and can be written as \(\log_{10}{x} = \log{x}\). The \(\log\) symbol written without a base means \(\log\) base \(\text{10}\).
Logarithmic laws:
- \(\log_{a}{x^{b}} = b \log_{a}{x} \qquad (x > 0)\)
- \(\log_{a}{x} = \frac{\log_{b}{x}}{\log_{b}{a}} \qquad (b > 0 \text{ and } b \ne 1)\)
- \(\log_{a}{xy} = \log_{a}{x} + \log_{a}{y} \qquad (x > 0 \text{ and } y > 0)\)
- \(\log_{a}{\frac{x}{y}} = \log_{a}{x} - \log_{a}{y} \qquad (x > 0 \text{ and } y > 0)\)
| Straight line function | Quadratic function | Exponential function | |
| Formula | \(y = ax + q\) | \(y = ax^{2}\) | \(y = b^{x}\) |
| Inverse | \(y = \frac{x}{a} - \frac{q}{a}\) | \(y = \pm \sqrt{\frac{x}{a}}\) | \(y = \log_{b}{x}\) |
| Inverse a function? | yes | no | yes |
| Graphs | 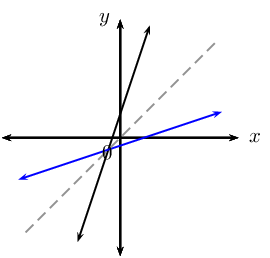 |
 |
 |
 |
 |
 |
End of chapter exercises
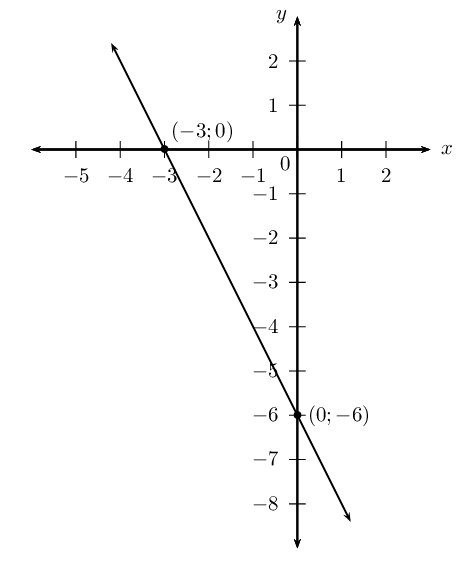
Given the straight line \(h\) with intercepts \((-3;0)\) and \((0;-6)\).
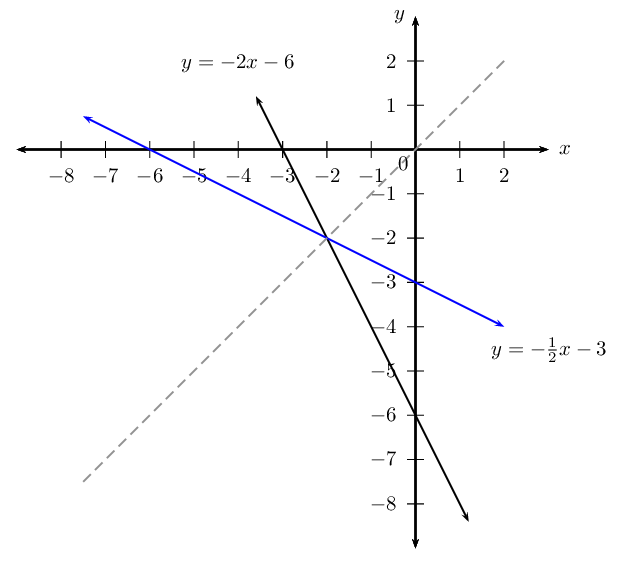
This gives the point \(S(-2;-2)\)
The value of the \(x\)-coordinate and the \(y\)-coordinate will always be the same since the point lies on the line \(y = x\).
The inverse of a function is \(f^{-1}(x) = 2x + 4\).
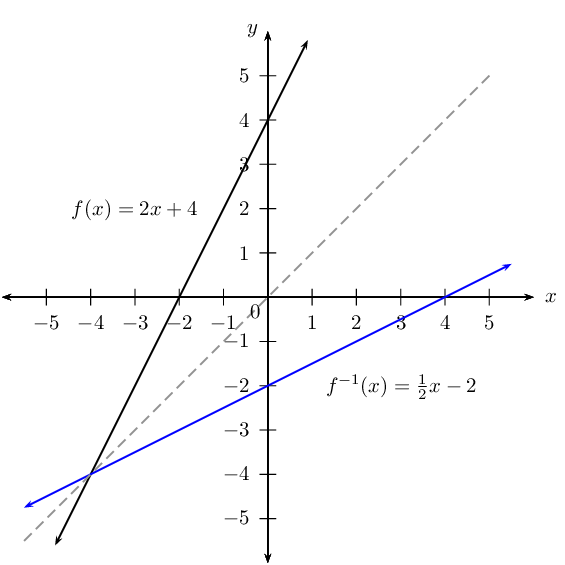
Increasing. As \(x\) increases, the function value increases. Alternative reason: gradient is positive, therefore function is increasing.
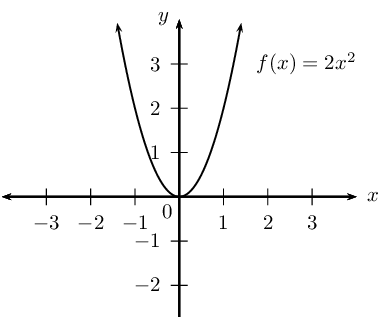
\(f\left(x\right)=2{x}^{2}\).
Draw the graph of \(f\) and state its domain and range.
The domain is: \(\{x: x \in \mathbb{R} \}\) and the range is: \(\{y: y \geq 0, y \in \mathbb{R} \}\).
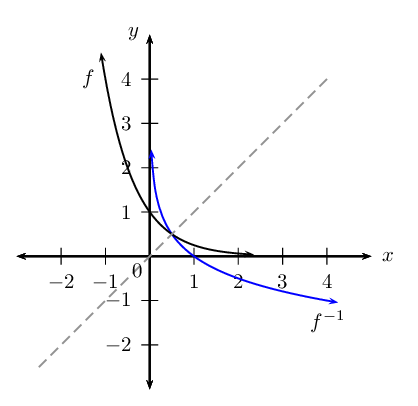
Determine the inverse and state its domain and range.
Domain: \(\{x: x \geq 0, x \in \mathbb{R} \}\), Range: \(\{y: y \in \mathbb{R} \}\).
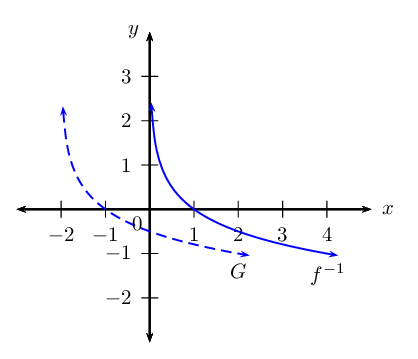
Given the function \(f(x) = \left( \frac{1}{4} \right)^{x}\).
Yes, the point \(\left( -\frac{1}{2}; 2 \right)\) does lie on \(f\).
\(y = \log_{\frac{1}{4}}{x}\) or \(y = - \log_{4}{x}\)
Consider the function \(h(x) = 3^{x}\).
Domain: \(\{x: x > 0, x \in \mathbb{R} \}\) and range: \(\{y: y \in \mathbb{R} \}\).
Consider the functions \(f(x) = 2^{x}\) and \(g(x) = x^{2}\).
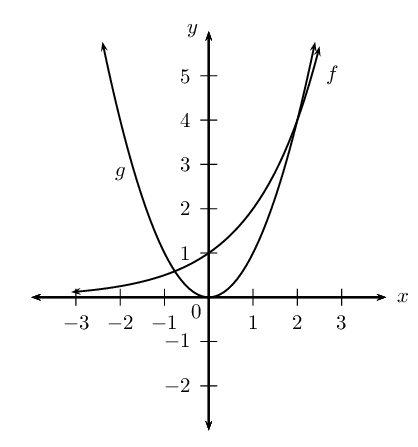
The graphs do not intersect at \(x = -1\).
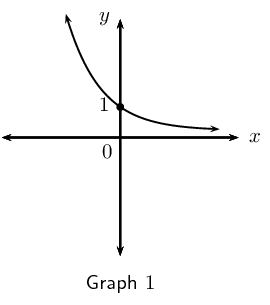
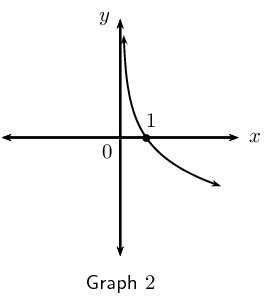
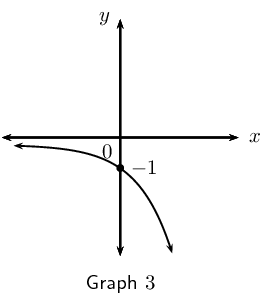
Below are three graphs and six equations. Write down the equation that best matches each of the graphs.
-
\(y={\log}_{3}x\)
-
\(y=-{\log}_{3}x\)
-
\(y={\log}_{\frac{1}{3}}x\)
-
\(y={3}^{x}\)
-
\(y={3}^{-x}\)
-
\(y=-{3}^{x}\)
Graph \(\text{1}\): \(y = 3^{-x}\)
Graph \(\text{2}\): \(y = - \log _{3} x\) or \(y = \log _{\frac{1}{3}}{x}\)
Graph \(\text{3}\): \(y = -3^{x}\)
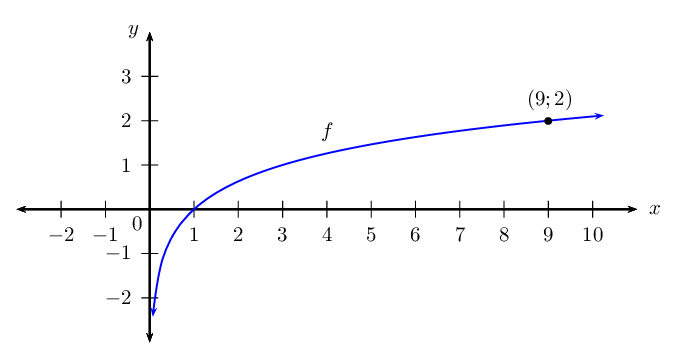
Given the graph of the function \(f: \enspace y = \log_{b}{x}\) passing through the point \((9;2)\).
It will take less than \(\text{10}\) years for the current rhino population to halve in size.
Which of the following graphs best illustrates the rhino population's decline? Motivate your answer.



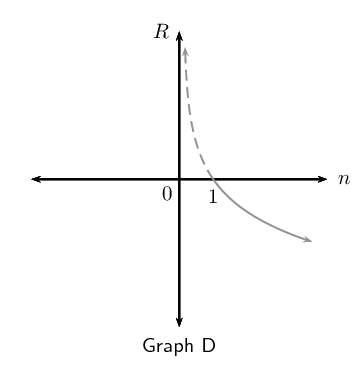
Important note: the graphs above have been drawn as a continuous curve to show a trend. Rhino population numbers are discrete values and should be plotted points.
Graph C
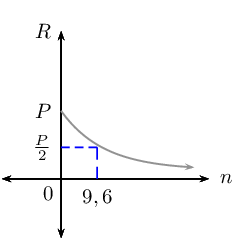
Currently \((n = 0)\) the rhino population is \(P\). After \(\text{9,6}\) years, it will have halved, \(\frac{P}{2}\). Note: the line in the graph indicates the trend, rhino population numbers are discrete values and should be plotted points.
At 8 a.m. a local celebrity tweets about his new music album to \(\text{100}\) of his followers. Five minutes later, each of his followers retweet his message to two of their friends. Five minutes after that, each friend retweets the message to another two friends. Assume this process continues.
\(\text{100} \qquad \text{100} \times 2 \qquad \text{100} \times 2^{2} \qquad \text{100} \times 2^{3}\)
This is a geometric sequence: \(r = 2\) and \(a = 100\).
Therefore \(T_{n} = 100 \times 2^{n-1}\).
\(\text{1}\) hour \(= 60\) minutes \(= 12 \times 5\), therefore \(n = 12\)
.\(\text{204 800}\) retweets.
Therefore, \(\frac{21}{12} = \text{1,75}\) hours.
Inverses (ENRICHMENT ONLY)
Given: \(g\left(x\right)=-1+\sqrt{x}\), find the inverse of \(g\left(x\right)\) in the form \({g}^{-1}\left(x\right)=...\)
Draw the graph of \(g^{-1}\).
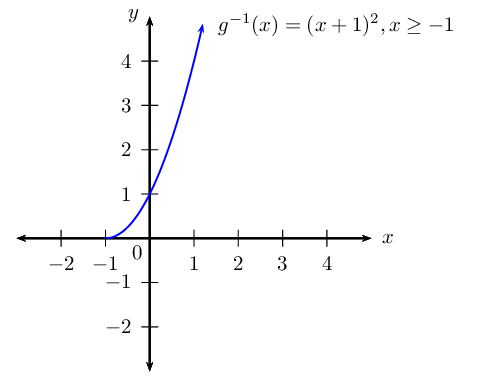
Use symmetry to draw the graph of \(g\) on the same set of axes.
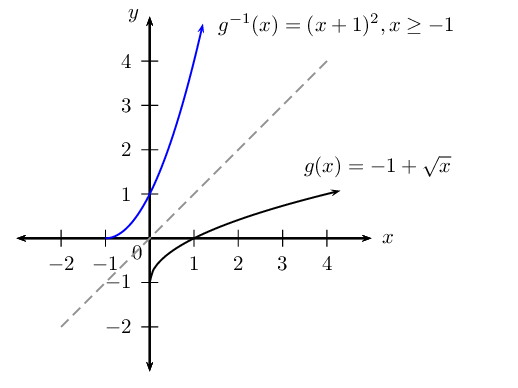
Is \(g^{-1}\) a function?
Yes. It passes vertical line test.
Give the domain and range of \(g^{-1}\).
Domain: \(\{x: x \ge -1, x \in \mathbb{R} \}\), Range: \(\{y: y \geq 0,y \in \mathbb{R} \}\).
The graph of the inverse of \(f\) is shown below:
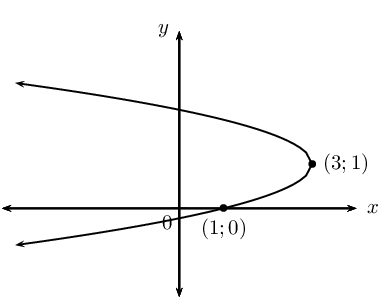
First use the information provided in the graph of the inverse:
\begin{align*} \text{Turning point: } & (3;1) \\ x-\text{intercept: } & (1;0) \end{align*}To get the turning point and intercepts of the function, we invert the given coordinates. Now we can use those coordinates to find the equation of the function:
Now find the equation of the function:
\begin{align*} \text{Turning point: } & (1;3) \\ x-\text{intercept: } & (0;1) \\ y & = a(x-p)^{2} + q \\ y & = a(x-1)^{2} + 3 \\ \text{Substitute } (0;1) \quad 1 & = a(0-1)^{2} + 3\\ a & = -\text{2}\\ \therefore y & = -2(x-1)^{2} + 3 \end{align*}Domain: \(\{x: x \in \mathbb{R} \}\) and range: \(\{y: y \leq 3,y \in \mathbb{R} \}\), Axis of symmetry: \(x =1\).
Given: \(k(x)=2{x}^{2}+1\)
If \((q;3)\) lies on \(k\), determine the value(s) of \(q\).
This gives the points \((-1;3)\) and \((1;3)\).
Sketch the graph of \(k\), label the point(s) \((q;3)\) on the graph.
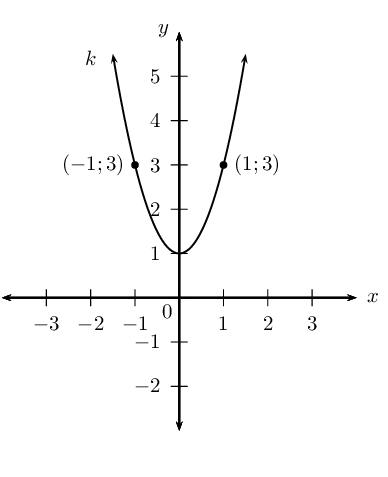
Find the equation of the inverse of \(k\) in the form \(y = \ldots\)
Sketch \(k\) and \(y = \sqrt{\frac{x-1}{2}}\) on the same system of axes.
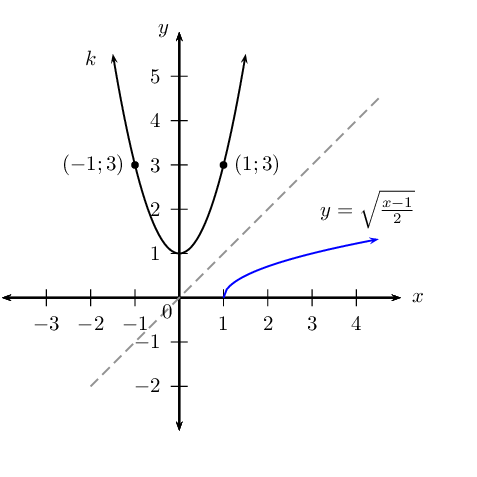
Determine the coordinates of the point on the graph of the inverse that is symmetrical to \((q;3)\) about the line \(y=x\).
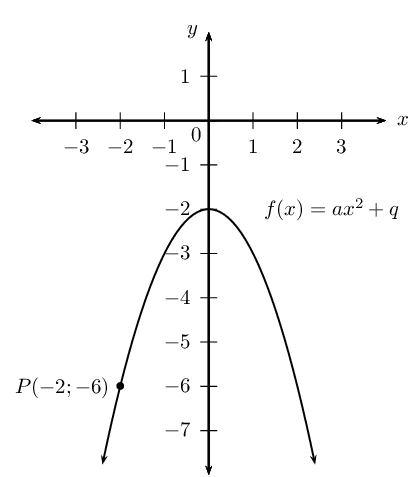
The sketch shows the graph of a parabola \(f(x) = ax^{2} + q\) passing through the point \(P(-2;-6)\).
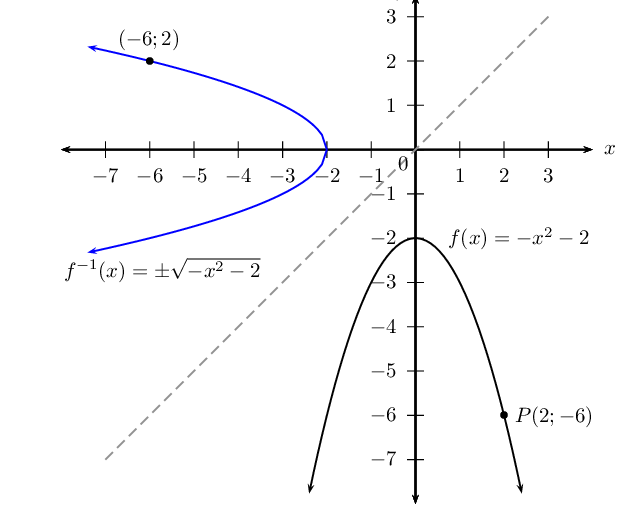
The inverse is a not a function. The turning point of the inverse is \((-2;0)\) and \(x\)-intercept is \((-2;0)\).
\[\text{Inverse}: \qquad \text{domain } \{x: x \le -2, x \in \mathbb{R} \} \quad \text{range } \{y: y \in \mathbb{R} \}\]Given the function \(H: y = x^{2} - 9\).
Determine the intercepts:
\begin{align*} \text{Let } x = 0: \quad y & = (0)^{2} - 9 \\ & = - 9 \\ \text{Let } y = 0: \quad 0 & = x^{2} - 9 \\ x^2 & = 9 \\ \therefore x & = \pm 3 \end{align*}The intercepts are \((0;-9)\) and \((-3;0),(3;0)\).
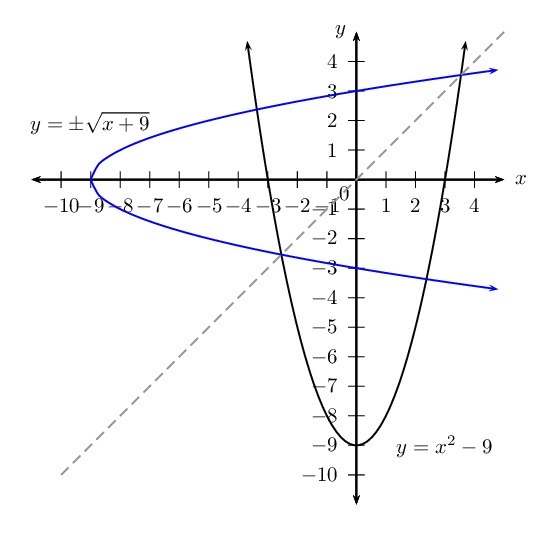
No. The inverse does not pass the vertical line test. It is a one-to-many relation.
If the domain of \(H\) is restricted to \(\{x: x \le 0 \}\), then the inverse is \(H^{-1}(x) = - \sqrt{x^{2} + 9} \quad (x \ge -9, y \le 0)\).
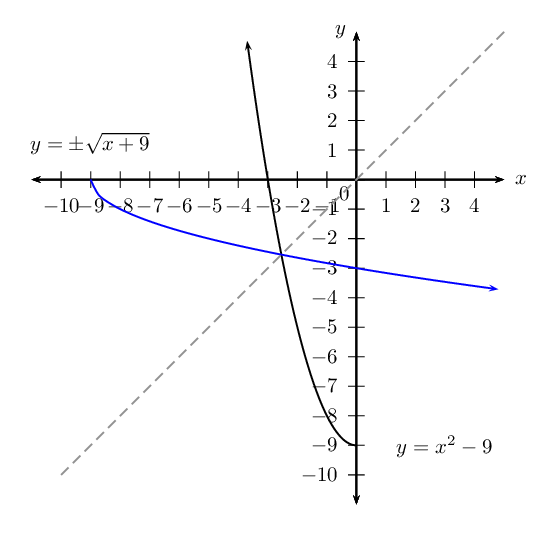
The graph of \(H^{-1}\) cuts a vertical line only once at any one time and therefore passes the vertical line test.
|
Previous
2.6 Exponential functions
|
Table of Contents |
Next
2.8 Enrichment: more on logarithms
|
