7.3 Equation of a tangent to a circle | Analytical geometry

7.3 Equation of a tangent to a circle (EMCHW)

On a suitable system of axes, draw the circle \(x^{2} + y^{2} = 20\) with centre at \(O(0;0)\).
Plot the point \(T(2;4)\).
Plot the point \(P(0;5)\). Draw \(PT\) and extend the line so that is cuts the positive \(x\)-axis.
Measure \(O\hat{T}P\).
Determine the gradient of the radius \(OT\).
Determine the gradient of \(PT\).
Prove that \(PT \perp OT\).
Plot the point \(S(2;-4)\) and join \(OS\).
Draw a tangent to the circle at \(S\).
Measure the angle between \(OS\) and the tangent line at \(S\).
Make a conjecture about the angle between the radius and the tangent to a circle at a point on the circle.
Complete the sentence: the product of the \(\ldots \ldots\) of the radius and the gradient of the \(\ldots \ldots\) is equal to \(\ldots \ldots\).

A circle with centre \(C(a;b)\) and a radius of \(r\) units is shown in the diagram above. \(D(x;y)\) is a point on the circumference and the equation of the circle is:

\[(x - a)^{2} + (y - b)^{2} = r^{2}\]

A tangent is a straight line that touches the circumference of a circle at only one place.

The tangent line \(AB\) touches the circle at \(D\).

The radius of the circle \(CD\) is perpendicular to the tangent \(AB\) at the point of contact \(D\).

\begin{align*} CD & \perp AB \\ \text{and } C\hat{D}A &= C\hat{D}B = \text{90} ° \end{align*}

The product of the gradient of the radius and the gradient of the tangent line is equal to \(-\text{1}\).

\[m_{CD} \times m_{AB} = - 1\]

How to determine the equation of a tangent:

Determine the equation of the circle and write it in the form \[(x - a)^{2} + (y - b)^{2} = r^{2}\]
From the equation, determine the coordinates of the centre of the circle \((a;b)\).
Determine the gradient of the radius: \[m_{CD} = \frac{y_{2} - y_{1}}{x_{2}- x_{1}}\]
The radius is perpendicular to the tangent of the circle at a point \(D\) so: \[m_{AB} = - \frac{1}{m_{CD}}\]
Write down the gradient-point form of a straight line equation and substitute \(m_{AB}\) and the coordinates of \(D\). Make \(y\) the subject of the equation. \[y - y_{1} = m(x - x_{1})\]

Worked example 12: Equation of a tangent to a circle

Determine the equation of the tangent to the circle \(x^{2} + y^{2} - 2y + 6x - 7 = 0\) at the point \(F(-2;5)\).

Write the equation of the circle in the form \((x - a)^{2} + (y - b)^{2} = r^{2}\)

Use the method of completing the square:

\begin{align*} x^{2} + y^{2} - 2y + 6x - 7 &= 0 \\ x^{2} + 6x + y^{2} - 2y &= 7 \\ (x^{2} + 6x + 9) - 9 + (y^{2} - 2y + 1) - 1 &= 7 \\ (x + 3)^{2} + (y - 1)^{2} &= 17 \end{align*}

Draw a sketch

The centre of the circle is \((-3;1)\) and the radius is \(\sqrt{17}\) units.

Determine the gradient of the radius \(CF\)

\begin{align*} m_{CF} &= \frac{y_{2} - y_{1}}{x_{2}- x_{1}}\\ &= \frac{5 - 1}{-2 + 3}\\ &= 4 \end{align*}

Determine the gradient of the tangent

Let the gradient of the tangent line be \(m\).

\begin{align*} m_{CF} \times m &= -1 \\ 4 \times m &= -1 \\ \therefore m &= - \frac{1}{4} \end{align*}

Determine the equation of the tangent to the circle

Write down the gradient-point form of a straight line equation and substitute \(m = - \frac{1}{4}\) and \(F(-2;5)\).

\begin{align*} y - y_{1} &= m (x - x_{1}) \\ y - y_{1} &= - \frac{1}{4} (x - x_{1}) \\ \text{Substitute } F(-2;5): \quad y - 5 &= - \frac{1}{4} (x - (-2)) \\ y - 5 &= - \frac{1}{4} (x + 2) \\ y &= - \frac{1}{4}x - \frac{1}{2} + 5 \\ &= - \frac{1}{4}x + \frac{9}{2} \end{align*}

Write the final answer

The equation of the tangent to the circle at \(F\) is \(y = - \frac{1}{4}x + \frac{9}{2}\).

temp text

Worked example 13: Equation of a tangent to a circle

The straight line \(y = x + 4\) cuts the circle \(x^{2} + y^{2} = 26\) at \(P\) and \(Q\).

Calculate the coordinates of \(P\) and \(Q\).
Sketch the circle and the straight line on the same system of axes. Label points \(P\) and \(Q\).
Determine the coordinates of \(H\), the mid-point of chord \(PQ\).
If \(O\) is the centre of the circle, show that \(PQ \perp OH\).
Determine the equations of the tangents to the circle at \(P\) and \(Q\).
Determine the coordinates of \(S\), the point where the two tangents intersect.
Show that \(S\), \(H\) and \(O\) are on a straight line.

Determine the coordinates of \(P\) and \(Q\)

Substitute the straight line \(y = x + 4\) into the equation of the circle and solve for \(x\):

\begin{align*} x^{2} + y^{2} &= 26 \\ x^{2} + (x + 4)^{2} &= 26 \\ x^{2} + x^{2} + 8x + 16 &= 26 \\ 2x^{2} + 8x - 10 &= 0 \\ x^{2} + 4x - 5 &= 0 \\ (x - 1)(x + 5) &= 0 \\ \therefore x = 1 &\text{ or } x = -5 \\ \text{If } x = 1 \quad y &= 1 + 4 = 5 \\ \text{If } x = -5 \quad y &= -5 + 4 = -1 \end{align*}

This gives the points \(P(-5;-1)\) and \(Q(1;5)\).

Draw a sketch

Determine the coordinates of the mid-point \(H\)

\begin{align*} H(x;y) &= \left( \frac{x_{1} + x_{2}}{2}; \frac{y_{1} + y_{2}}{2} \right) \\ &= \left( \frac{1 - 5}{2}; \frac{5 - 1}{2} \right) \\ &= \left( \frac{-4}{2}; \frac{4}{2} \right) \\ &= \left( -2; 2 \right) \end{align*}

Show that \(OH\) is perpendicular to \(PQ\)

We need to show that the product of the two gradients is equal to \(-\text{1}\). From the given equation of \(PQ\), we know that \(m_{PQ} = 1\).

\begin{align*} m_{OH} &= \frac{2 - 0}{-2 - 0} \\ &= - 1 \\ & \\ m_{PQ} \times m_{OH} &= - 1 \\ & \\ \therefore PQ & \perp OH \end{align*}

Determine the equations of the tangents at \(P\) and \(Q\)

Tangent at \(P\):

Determine the gradient of the radius \(OP\):

\begin{align*} m_{OP} &= \frac{-1 - 0}{- 5 - 0} \\ &= \frac{1}{5} \end{align*}

The tangent of a circle is perpendicular to the radius, therefore we can write:

\begin{align*} \frac{1}{5} \times m_{P} &= -1 \\ \therefore m_{P} &= - 5 \end{align*}

Substitute \(m_{P} = - 5\) and \(P(-5;-1)\) into the equation of a straight line.

\begin{align*} y - y_{1} &= - 5 (x - x_{1}) \\ \text{Substitute } P(-5;-1): \quad y + 1 &= - 5 (x + 5) \\ y &= -5x - 25 - 1 \\ &= -5x - 26 \end{align*}

Tangent at \(Q\):

Determine the gradient of the radius \(OQ\):

\begin{align*} m_{OQ} &= \frac{5 - 0}{1 - 0} \\ &= 5 \end{align*}

The tangent of a circle is perpendicular to the radius, therefore we can write:

\begin{align*} 5 \times m_{Q} &= -1 \\ \therefore m_{Q} &= - \frac{1}{5} \end{align*}

Substitute \(m_{Q} = - \frac{1}{5}\) and \(Q(1;5)\) into the equation of a straight line.

\begin{align*} y - y_{1} &= - \frac{1}{5} (x - x_{1}) \\ \text{Substitute } Q(1;5): \quad y - 5 &= - \frac{1}{5} (x - 1) \\ y &= - \frac{1}{5}x + \frac{1}{5} + 5 \\ &= - \frac{1}{5}x + \frac{26}{5} \end{align*}

The equations of the tangents are \(y = -5x - 26\) and \(y = - \frac{1}{5}x + \frac{26}{5}\).

Determine the coordinates of \(S\)

Equate the two linear equations and solve for \(x\):

\begin{align*} -5x - 26 &= - \frac{1}{5}x + \frac{26}{5} \\ -25x - 130 &= - x + 26 \\ -24x &= 156 \\ x &= - \frac{156}{24} \\ &= - \frac{13}{2} \\ \text{If } x = - \frac{13}{2} \quad y &= - 5 \left( - \frac{13}{2} \right) - 26 \\ &= \frac{65}{2} - 26 \\ &= \frac{13}{2} \end{align*}

This gives the point \(S \left( - \frac{13}{2}; \frac{13}{2} \right)\).

Show that \(S\), \(H\) and \(O\) are on a straight line

We need to show that there is a constant gradient between any two of the three points. We have already shown that \(PQ\) is perpendicular to \(OH\), so we expect the gradient of the line through \(S\), \(H\) and \(O\) to be \(-\text{1}\).

\begin{align*} m_{SH} &= \dfrac{\frac{13}{2} - 2}{- \frac{13}{2} + 2} \\ &= - 1 \end{align*}\begin{align*} m_{SO} &= \dfrac{\frac{13}{2} - 0}{- \frac{13}{2} - 0} \\ &= - 1 \end{align*}

Therefore \(S\), \(H\) and \(O\) all lie on the line \(y=-x\).

Worked example 14: Equation of a tangent to a circle

Determine the equations of the tangents to the circle \(x^{2} + (y - 1)^{2} = 80\), given that both are parallel to the line \(y = \frac{1}{2}x + 1\).

Draw a sketch

The tangents to the circle, parallel to the line \(y = \frac{1}{2}x + 1\), must have a gradient of \(\frac{1}{2}\). From the sketch we see that there are two possible tangents.

Determine the coordinates of \(A\) and \(B\)

To determine the coordinates of \(A\) and \(B\), we must find the equation of the line perpendicular to \(y = \frac{1}{2}x + 1\) and passing through the centre of the circle. This perpendicular line will cut the circle at \(A\) and \(B\).

Notice that the line passes through the centre of the circle.

To determine the coordinates of \(A\) and \(B\), we substitute the straight line \(y = - 2x + 1\) into the equation of the circle and solve for \(x\):

\begin{align*} x^{2} + (y-1)^{2} &= 80 \\ x^{2} + \left( - 2x + 1 - 1 \right)^{2} &= 80 \\ x^{2} + 4x^{2} &= 80 \\ 5x^{2} &= 80 \\ x^{2} &= 16 \\ \therefore x &= \pm 4 \\ \text{If } x = 4 \quad y &= - 2(4) + 1 = - 7 \\ \text{If } x = -4 \quad y &= - 2(-4) + 1 = 9 \end{align*}

This gives the points \(A(-4;9)\) and \(B(4;-7)\).

Determine the equations of the tangents to the circle

Tangent at \(A\):

\begin{align*} y - y_{1} &= \frac{1}{2} (x - x_{1}) \\ y - 9 &= \frac{1}{2} (x + 4 ) \\ y &= \frac{1}{2} x + 11 \end{align*}

Tangent at \(B\):

\begin{align*} y - y_{1} &= \frac{1}{2} (x - x_{1}) \\ y + 7 &= \frac{1}{2} (x - 4 ) \\ y &= \frac{1}{2}x - 9 \end{align*}

The equation of the tangent at point \(A\) is \(y = \frac{1}{2}x + 11\) and the equation of the tangent at point \(B\) is \(y = \frac{1}{2}x - 9\).

Worked example 15: Equation of a tangent to a circle

Determine the equations of the tangents to the circle \(x^{2} + y^{2} = 25\), from the point \(G(-7;-1)\) outside the circle.

Draw a sketch

Consider where the two tangents will touch the circle

Let the two tangents from \(G\) touch the circle at \(F\) and \(H\).

\begin{align*} OF = OH &= \text{5}\text{ units} \quad (\text{equal radii}) \\ OG &= \sqrt{(0 + 7)^{2} + (0 + 1)^2} \\ &= \sqrt{50} \\ GF &= \sqrt{ (x + 7)^{2} + (y + 1)^2} \\ \therefore GF^{2} &= (x + 7)^{2} + (y + 1)^2 \\ \text{And } G\hat{F}O = G\hat{H}O &= \text{90} ° \end{align*}

Consider \(\triangle GFO\) and apply the theorem of Pythagoras:

\begin{align*} GF^{2} + OF^{2} &= OG^{2} \\ \left( x + 7 \right)^{2} + \left( y + 1 \right)^{2} + 5^{2} &= \left( \sqrt{50} \right)^{2} \\ x^{2} + 14x + 49 + y^{2} + 2y + 1 + 25 &= 50 \\ x^{2} + 14x + y^{2} + 2y + 25 &= 0 \ldots \ldots (1) \\ \text{Substitute } y^{2} = 25 - x^{2} & \text{ into equation } (1) \\ \quad x^{2} + 14x + \left( 25 - x^{2} \right) + 2\left( \sqrt{25 - x^{2}} \right) + 25 &= 0 \\ 14x + 50 &= - 2\left( \sqrt{25 - x^{2}} \right) \\ 7x + 25 &= - \sqrt{25 - x^{2}} \\ \text{Square both sides: } (7x + 25)^{2} &= \left( - \sqrt{25 - x^{2}} \right)^{2} \\ 49x^{2} + 350x + 625 &= 25 - x^{2} \\ 50x^{2} + 350x + 600 &= 0 \\ x^{2} + 7x + 12 &= 0 \\ (x + 3)(x + 4) &= 0 \\ \therefore x = -3 & \text{ or } x = -4 \\ \text{At } F: x = -3 \quad y &= - \sqrt{25 - (-3)^{2}} = - \sqrt{16} = - 4 \\ \text{At } H: x = -4 \quad y &= \sqrt{25 - (-4)^{2}} = \sqrt{9} = 3 \end{align*}

Note: from the sketch we see that \(F\) must have a negative \(y\)-coordinate, therefore we take the negative of the square root. Similarly, \(H\) must have a positive \(y\)-coordinate, therefore we take the positive of the square root.

This gives the points \(F(-3;-4)\) and \(H(-4;3)\).

Tangent at \(F\):

\begin{align*} m_{FG} &= \frac{-1 + 4}{-7 + 3} \\ &= - \frac{3}{4} \end{align*}\begin{align*} y - y_{1} &= m (x - x_{1}) \\ y - y_{1} &= - \frac{3}{4} (x - x_{1}) \\ y + 1 &= - \frac{3}{4} (x + 7) \\ y &= - \frac{3}{4}x - \frac{21}{4} - 1 \\ y &= - \frac{3}{4}x - \frac{25}{4} \end{align*}

Tangent at \(H\):

\begin{align*} m_{HG} &= \frac{-1 - 3}{-7 + 4} \\ &= \frac{4}{3} \end{align*}\begin{align*} y + 1 &= \frac{4}{3} \left(x + 7 \right) \\ y &= \frac{4}{3}x + \frac{28}{3} - 1 \\ y &= \frac{4}{3}x + \frac{25}{3} \end{align*}

Write the final answer

The equations of the tangents to the circle are \(y = - \frac{3}{4}x - \frac{25}{4}\) and \(y = \frac{4}{3}x + \frac{25}{3}\).

Video: 293H

Equation of a tangent to a circle

Textbook Exercise 7.5

A circle with centre \((8;-7)\) and the point \((5;-5)\) on the circle are given. Determine the gradient of the radius.

Given:

the centre of the circle \((a;b) = (8;-7)\)
a point on the circumference of the circle \((x_1;y_1) = (5;-5)\)

Required:

the gradient of the radius, \(m\)

\begin{align*} m & = \frac{y_2 - y_1}{x_2 - x_1}\\ & = \frac{-5+7}{5-8}\\ & = - \frac{2}{3} \end{align*}

The gradient of the radius is \(m = - \frac{2}{3}\).

Determine the gradient of the tangent to the circle at the point \((5;-5)\).

The tangent to the circle at the point \((5;-5)\) is perpendicular to the radius of the circle to that same point: \(m \times m_{\bot} = -1\)

\begin{align*} m_{\bot} & = - \frac{1}{m}\\ & = \frac{-1}{- \frac{2}{3} }\\ & = \frac{3}{2} \end{align*}

The gradient for the tangent is \(m_{\bot} = \frac{3}{2}\).

Find the gradient of the radius at the point \((2;2)\) on the circle.

Given:

the equation for the circle \(\left(x + 4\right)^{2} + \left(y + 8\right)^{2} = 136\)
a point on the circumference of the circle \((x_1;y_1) = (2;2)\)

Required:

the gradient of the radius, \(m\)

The coordinates of the centre of the circle are \((-4;-8)\).

Draw a rough sketch:

The gradient for this radius is \(m = \frac{5}{3}\).

Determine the gradient of the tangent to the circle at the point \((2;2)\).

Given:

The tangent to the circle at the point \((2;2)\) is perpendicular to the radius, so \(m \times m_{\text{tangent}} = -1\)

\begin{align*} m_{\text{tangent}} & = - \frac{1}{m}\\ & = - \frac{1}{\frac{5}{3} }\\ & = - \frac{3}{5} \end{align*}

The gradient for the tangent is \(m_{\text{tangent}} = - \frac{3}{5}\).

Given a circle with the central coordinates \((a;b) = (-9;6)\). Determine the equation of the tangent to the circle at the point \((-2;5)\).

\begin{align*} m_r & = \frac{y_1 - y_0}{x_1 - x_0} \\ & = \frac{5 - 6 }{ -2 -(-9)} \\ & = - \frac{1}{7} \end{align*}

The tangent is perpendicular to the radius, therefore \(m \times m_{\bot} = -1\).

\begin{align*} m & = - \frac{1}{m_r} \\ & = \frac{1}{ \frac{1}{7} } \\ & = 7 \end{align*}

Write down the equation of a straight line and substitute \(m = 7\) and \((-2;5)\).

\begin{align*} y_1 & =m x_1 + c\\ 5 & = 7 (-2) + c \\ c & = 19 \end{align*}

The equation of the tangent to the circle is \(y = 7 x + 19\).

Given the diagram below:

Determine the equation of the tangent to the circle with centre \(C\) at point \(H\).

Given:

the centre of the circle \(C(a;b) = (1;5)\)
a point on the circumference of the circle \(H(-2;1)\)

Required:

the equation for the tangent to the circle in the form \(y = mx + c\)

Calculate the gradient of the radius:

\begin{align*} m_r & = \frac{y_1 - y_0}{x_1 - x_0} \\ & = \frac{1 - 5}{-2 - 1 } \\ & = \frac{-4}{-3 } \\ & = \frac{4}{3} \end{align*} \begin{align*} m_r \times m &= -1 \\ m & = - \frac{1}{m_r} \\ & = - \frac{1}{\frac{4}{3} } \\ & = - \frac{3}{4} \end{align*}

Equation of the tangent:

\begin{align*} y & = m x + c\\ 1 & = - \frac{3}{4} (-2) + c \\ 1 & = \frac{3}{2} + c \\ c & = - \frac{1}{2} \end{align*}

The equation for the tangent to the circle at the point \(H\) is:

\begin{align*} y & = - \frac{3}{4} x - \frac{1}{2} \end{align*}

Given the point \(P(2;-4)\) on the circle \(\left(x - 4\right)^{2} + \left(y + 5\right)^{2} = 5\). Find the equation of the tangent at \(P\).

Given:

the equation for the circle \(\left(x - 4\right)^{2} + \left(y + 5\right)^{2} = 5\)
a point on the circumference of the circle \(P(2;-4)\)

Required:

the equation of the tangent in the form \(y = mx + c\)

The coordinates of the centre of the circle are \((a;b) = (4;-5)\).

The gradient of the radius:

\begin{align*} m_r & = \frac{y_1 - y_0}{x_1 - x_0} \\ & = \frac{ -4 - (-5)}{2 - 4} \\ & = - \frac{1}{2} \end{align*} \begin{align*} m \times m_{\bot} & = -1 \\ \therefore m_{\bot} & = - \frac{1}{m_r} \\ & = \frac{1}{\frac{1}{2}} \\ & = 2 \end{align*}

Equation of the tangent:

\begin{align*} y & = m_{\bot} x + c\\ -4 & = 2 (2) + c \\ c & = -8 \end{align*}

The equation of the tangent to the circle is

\begin{align*} y & = 2 x - 8 \end{align*}

Determine the equation of the circle.

Use the distance formula to determine the length of the radius:

\begin{align*} r & = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \\ & = \sqrt{(2+4)^2 + (-2-8)^2} \\ & = \sqrt{(6)^2 + (-10)^2} \\ & = \sqrt{136} \end{align*}

Write down the general equation of a circle and substitute \(r\) and \(H(2;-2)\):

\begin{align*} (x-a)^2+ (y-b)^2 & = r^2 \\ (x - (-4))^2 + (y-(8))^2 & = (\sqrt{136})^2 \\ \left(x + 4\right)^{2} + \left(y - 8\right)^{2} & = 136 \end{align*}

The equation of the circle is \(\left(x + 4\right)^{2} + \left(y - 8\right)^{2} = 136\).

Determine the value of \(m\).

Substitute the \(Q(-10;m)\) and solve for the \(m\) value.

\begin{align*} \left(x + 4\right)^{2} + \left(y - 8\right)^{2} & = 136 \\ \left(-10 + 4\right)^{2} + \left(m - 8\right)^{2} & = 136 \\ 36 + \left(m - 8\right)^{2} & = 136 \\ m^{2} - 16 m + 100 & = 136 \\ m^{2} - 16 m - 36 & = 0 \\ (m+2)(m-18) & = 0 \end{align*}

The solution shows that \(y = -2\) or \(y = 18\). From the graph we see that the \(y\)-coordinate of \(Q\) must be positive, therefore \(Q(-10;18)\).

Determine the equation of the tangent to the circle at point \(Q\).

Calculate the gradient of the radius:

\begin{align*} m_r & = \frac{y_2 - y_0}{x_2 - x_0} \\ & = \frac{18 - 8}{-10 + 4 } \\ & = - \frac{10}{6 } \\ & = - \frac{5}{3} \end{align*}

The radius is perpendicular to the tangent, so \(m \times m_{\bot} = -1\).

\begin{align*} m_{\bot} & = - \frac{1}{m_r} \\ & = \frac{1}{\frac{5}{3}} \\ & = \frac{3}{5} \end{align*}

The equation for the tangent to the circle at the point \(Q\) is:

\begin{align*} y & = m_{\bot} x + c\\ 18 & = \frac{3}{5} (-10) + c \\ 18 & = -6 + c \\ c & = 24 \end{align*} \begin{align*} y & = \frac{3}{5} x + 24 \end{align*}

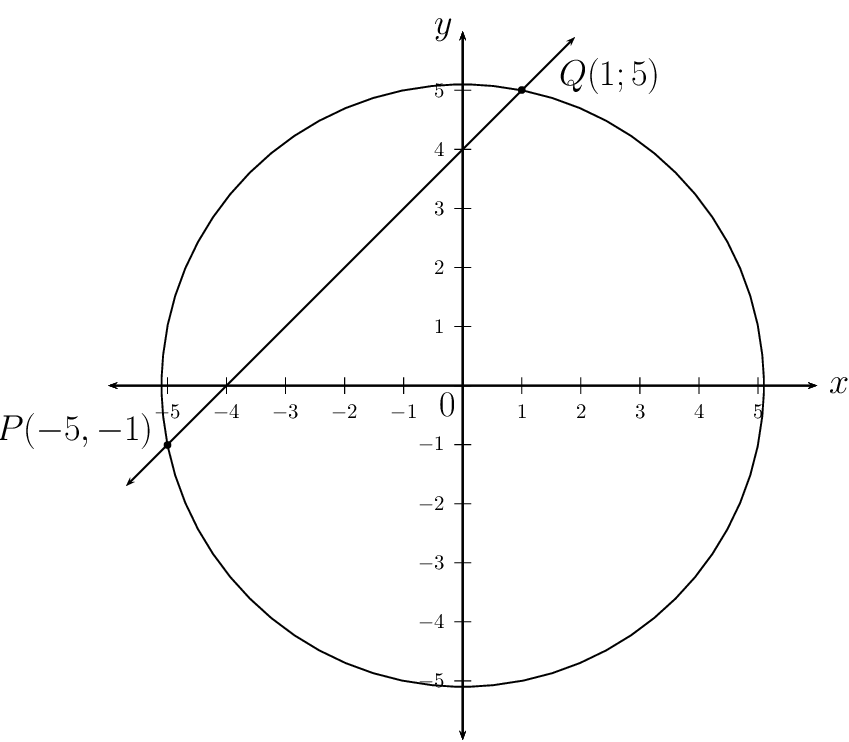
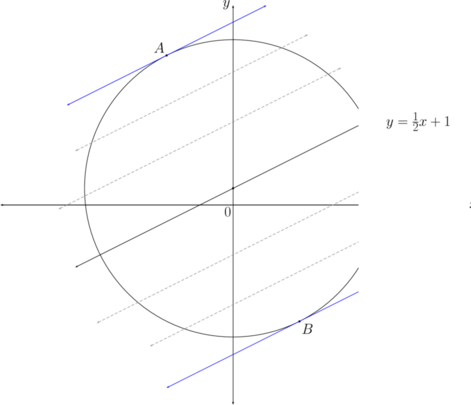
Calculate the coordinates of \(P\) and \(Q\).

Substitute the straight line \(y = x + 2\) into the equation of the circle and solve for \(x\):

\begin{align*} x^{2} + y^{2} &= 20 \\ x^{2} + (x + 2)^{2} &= 20 \\ x^{2} + x^{2} + 4x + 4 &= 20 \\ 2x^{2} + 4x - 16 &= 0 \\ x^{2} + 2x - 8 &= 0 \\ (x - 2)(x + 4) &= 0 \\ \therefore x = 2 &\text{ or } x = -4 \\ \text{If } x = 2 \quad y &= 2 + 2 = 4 \\ \text{If } x = -4 \quad y &= -4 + 2 = -2 \end{align*}

This gives the points \(P(-4;-2)\) and \(Q(2;4)\).

Determine the length of \(PQ\).

\begin{align*} PQ &= \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^2} \\ &= \sqrt{(-4 -2)^{2} + (-2-4 )^2} \\ &= \sqrt{(-6)^{2} + (-6)^2} \\ &= \sqrt{36 + 36} \\ &= \sqrt{36 \cdot 2} \\ &= 6\sqrt{2} \end{align*}

Determine the coordinates of \(M\), the mid-point of chord \(PQ\).

\begin{align*} M(x;y) &= \left( \frac{x_{1} + x_{2}}{2}; \frac{y_{1} + y_{2}}{2} \right) \\ &= \left( \frac{-4 + 2}{2}; \frac{-2 + 4}{2} \right) \\ &= \left( \frac{-2}{2}; \frac{2}{2} \right) \\ &= \left( -1; 1 \right) \end{align*}

If \(O\) is the centre of the circle, show that \(PQ \perp OM\).

\begin{align*} m_{PQ} &= \frac{4 - (-2)}{2 - (-4)} \\ &= \frac{6}{6} \\ &= 1 \\ & \\ m_{OM} &= \frac{1 - 0}{-1 - 0} \\ &= - 1 \\ m_{PQ} \times m_{OM} &= - 1 \\ & \\ \therefore PQ & \perp OM \end{align*}

Determine the equations of the tangents to the circle at \(P\) and \(Q\).

Tangent at \(P\):

Determine the gradient of the radius \(OP\):

\begin{align*} m_{OP} &= \frac{y_{2} - y_{1}}{x_{2}- x_{1}} \\ &= \frac{-2 - 0}{- 4 - 0} \\ &= \frac{1}{2} \end{align*}

Let the gradient of the tangent at \(P\) be \(m_{P}\). The tangent of a circle is perpendicular to the radius, therefore we can write:

\begin{align*} m_{OP} \times m_{P} &= -1 \\ \frac{1}{2} \times m_{P} &= -1 \\ \therefore m_{P} &= - 2 \end{align*}

Substitute \(m_{P} = - 2\) and \(P(-4;-2)\) into the equation of a straight line.

\begin{align*} y - y_{1} &= m (x - x_{1}) \\ y - y_{1} &= - 2 (x - x_{1}) \\ \text{Substitute } P(-4;-2): \quad y + 2 &= - 2 (x + 4) \\ y &= -2x - 8 - 2 \\ &= -2x - 10 \end{align*}

Tangent at \(Q\):

Determine the gradient of the radius \(OQ\):

\begin{align*} m_{OQ} &= \frac{y_{2} - y_{1}}{x_{2}- x_{1}} \\ &= \frac{4 - 0}{2 - 0} \\ &= 2 \end{align*}

Let the gradient of the tangent at \(Q\) be \(m_{Q}\). The tangent of a circle is perpendicular to the radius, therefore we can write:

\begin{align*} m_{OQ} \times m_{Q} &= -1 \\ 2 \times m_{Q} &= -1 \\ \therefore m_{Q} &= - \frac{1}{2} \end{align*}

Substitute \(m_{Q} = - \frac{1}{2}\) and \(Q(2;4)\) into the equation of a straight line.

\begin{align*} y - y_{1} &= m (x - x_{1}) \\ y - y_{1} &= - \frac{1}{2} (x - x_{1}) \\ \text{Substitute } Q(2;4): \quad y - 4 &= - \frac{1}{2} (x - 2) \\ y &= - \frac{1}{2}x + 1 + 4 \\ &= - \frac{1}{2}x + 5 \end{align*}

Therefore the equations of the tangents to the circle are \(y = -2x - 10\) and \(y = - \frac{1}{2}x + 5\).

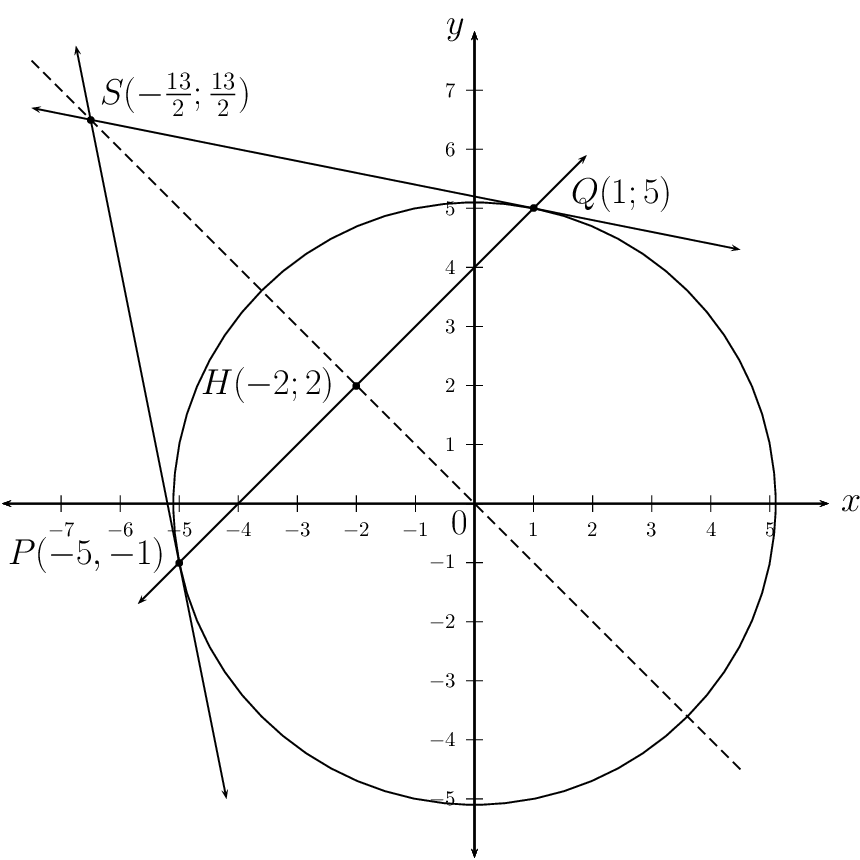
Determine the coordinates of \(S\), the point where the two tangents intersect.

Equate the two linear equations and solve for \(x\):

\begin{align*} -2x - 10 &= - \frac{1}{2}x + 5 \\ -4x - 20 &= - x + 10 \\ -3x &= 30 \\ x &= - 10 \\ \text{If } x = - 10 \quad y &= - 2 \left( - 10 \right) - 10 \\ &= 10 \end{align*}

This gives the point \(S \left( - 10;10 \right)\).

Show that \(PS = QS\).

\begin{align*} PS &= \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^2} \\ &= \sqrt{(-4 -(-10))^{2} + (-2 - 10)^2} \\ &= \sqrt{(6)^{2} + (-12)^2} \\ &= \sqrt{36 + 144} \\ &= \sqrt{180} \end{align*} \begin{align*} QS &= \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^2} \\ &= \sqrt{(2 -(-10))^{2} + (4 - 10)^2} \\ &= \sqrt{(12)^{2} + (-6)^2} \\ &= \sqrt{144 + 36} \\ &= \sqrt{180} \end{align*}

Determine the equations of the two tangents to the circle, both parallel to the line \(y + 2x = 4\).

The tangent at \(P\), \(y = -2x - 10\), is parallel to \(y = - 2x + 4\). To find the equation of the second parallel tangent:

\begin{align*} y &= -2x + 4 \\ \therefore m &= -2 \\ \therefore m_{\text{radius}}&= \frac{1}{2} \\ \text{Eqn. of radius: } y &= \frac{1}{2}x \ldots(1) \\ \text{Substitute } (1): \quad x^{2} + y^{2} &= 20 \\ x^{2} + \left( \frac{1}{2}x \right)^{2} &= 20 \\ x^{2} + \frac{1}{4}x^{2} &= 20 \\ \frac{5}{4}x^{2} &= 20 \\ x^{2} &= 16 \\ x &= \pm 4 \\ \text{If } x = 4, y &= 2 \\ \text{Substitute } (4;2): \quad y &= -2x + c \\ 2 &=-2(4) + c \\ 10 &= c \\ y &= -2x + 10 \end{align*}

7.2 Equation of a circle

Table of Contents

7.4 Summary