\(x^{2} + y^{2} = 16\)
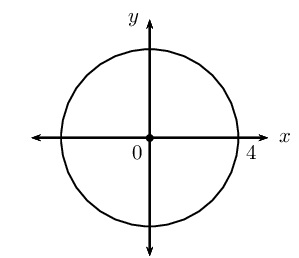
This gives the points \(\left( 1; \sqrt{15} \right)\) and \(\left( 1; -\sqrt{15} \right)\).
|
Previous
7.1 Revision
|
Next
7.3 Equation of a tangent to a circle
|
What object do the points form?
| Line segment | Distance \((cm)\) |
| \(DO\) | |
| \(EO\) | |
| \(FO\) | |
| \(GO\) | |
| \(HO\) | |
| \(IO\) | |
| \(JO\) | |
| \(KO\) |
| Line segment | Distance |
| \(DO\) | |
| \(EO\) | |
| \(FO\) | |
| \(GO\) | |
| \(HO\) | |
| \(IO\) | |
| \(JO\) | |
| \(KO\) |

A circle is the set of all points that are an equal distance (radius) from a given point (centre). In other words, every point on the circumference of a circle is equidistant from its centre.
The radius of a circle is the distance from the centre of a circle to any point on the circumference.
A diameter of a circle is any line passing through the centre of the circle which connects two points on the circle. The diameter is also the name given to the maximum distance between two points on a circle.
Consider a point \(P\left( x;y \right)\) on the circumference of a circle of radius \(r\) with centre at \(O\left( 0;0 \right)\).

In \(\triangle OPQ\):
\begin{align*} O{P}^{2} & = P{Q}^{2}+O{Q}^{2} \quad \left( \text{Pythagoras} \right) \\ OP & = r \\ PQ & = y - 0 \\ OQ & = x - 0 \\ {r}^{2} & = {\left( y - 0\right)}^{2}+{\left( x - 0 \right)}^{2} \\ \therefore {r}^{2} & = x^{2} + y^{2} \end{align*}Equation of a circle with centre at the origin:
If \(P(x;y)\) is a point on a circle with centre \(O(0;0)\) and radius \(r\), then the equation of the circle is:
\[x^{2} + y^{2} = r^{2}\]Circle symmetry
A circle with centre \((0;0)\) is symmetrical about the origin: for every point \((x;y)\) on the circumference of a circle, there is also the point \((-x;-y)\).
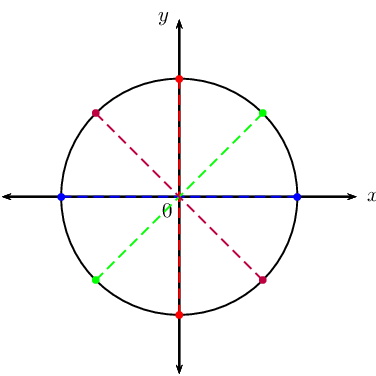
A circle centred on the origin is also symmetrical about the \(x\)- and \(y\)-axis. Is a circle centred on the origin symmetrical about the lines \(y = x\) and \(y = -x\)? How many lines of symmetry does a circle have?
Given: circle with centre \(O(0;0)\) and a radius of \(\text{3}\) units.
Write down the general form of the equation of a circle with centre \((0;0)\):
\begin{align*} x^{2} + y^{2} &= r^{2} \\ \text{Substitute } r = 3: \quad x^{2} + y^{2} &= (3)^{2} \\ x^{2} + y^{2} &= 9 \end{align*}Substitute the \(x\)-coordinate and the \(y\)-coordinate into the left-hand side of the equation and show that it is equal to the right-hand side:
\begin{align*} \text{LHS } &= x^{2} + y^{2} \\ &= \left( - \sqrt{4} \right)^{2} + \left( \sqrt{5} \right)^{2} \\ &= 4 + 5 \\ &= 9 \\ &= r^{2} \\ &= \text{RHS } \end{align*}Therefore, \(T \left( - \sqrt{4}; \sqrt{5} \right)\) lies on the circle \(x^{2} + y^{2} = 9\).
A circle with centre \(O(0;0)\) passes through the points \(P(-5;5)\) and \(Q(5;-5)\).
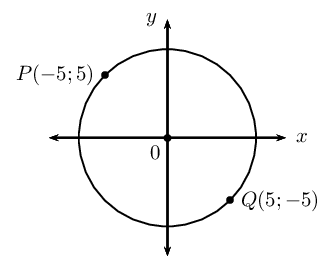
Write down the general form of the equation of a circle with centre \((0;0)\) and substitute \(P(-5;5)\):
\begin{align*} x^{2} + y^{2} &= r^{2} \\ (-5)^{2} + (5)^{2} &= r^{2} \\ 25 + 25 &= r^{2} \\ 50 &= r^{2} \\ \therefore r &= \sqrt{50} \quad (r \text{ is always positive}) \\ r &= 5\sqrt{2} \text{ units} \end{align*}Therefore, the equation of the circle passing through \(P\) and \(Q\) is \(x^{2} + y^{2} = 50\).
Use the distance formula to determine the distance between the two points.
\begin{align*} PQ &= \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^2} \\ &= \sqrt{(5 - (-5))^{2} + (-5 - 5)^2} \\ &= \sqrt{(10)^{2} + (-10)^2} \\ &= \sqrt{100 + 100} \\ &= \sqrt{100 \cdot 2} \\ &= 10\sqrt{2} \text{ units} \end{align*}Since \(PQ\) connects two points, \(P\) and \(Q\), on the circle and is a line of length \(10 \sqrt{2}\) units, \(PQ\) is a diameter of the circle.
Alternative method \(\text{1}\): Use symmetry to show that \(PQ\) is a diameter of the circle.
The diameter is the name given to the maximum distance between two points on a circle; this means that the two points must lie opposite each other with respect to the centre.
Using symmetry about the origin, we know that \((x;y)\) lies opposite \((-x;-y)\) on the circle and vice versa:
Therefore, \(PQ\) is a diameter of the circle.
Alternative method \(\text{2}\): Show that \(PQ\) passes through the centre.
Determine the equation of \(PQ\) and show that it passes through the origin.
\begin{align*} \dfrac{y - y_{Q}}{x - x_{Q}} &= \dfrac{y_{P} - y_{Q}}{x_{P} - x_{Q}} \\ \dfrac{y + 5}{x - 5} &= \dfrac{5 + 5}{-5 - 5} \\ \dfrac{y + 5}{x - 5} &= \dfrac{10}{-10} \\ y + 5 &= -(x - 5) \\ y &= -x + 5 - 5 \\ y &= -x \end{align*}\(\therefore (0;0)\) lines on the line \(PQ\).
Therefore, \(PQ\) passes through the centre and is a diameter of the circle.
Given a circle with centre \(O(0;0)\) and a radius of \(\sqrt{45}\) units. Determine the possible coordinates of the point(s) on the circle which have an \(x\)-value that is twice the \(y\)-value.
To calculate the possible coordinates of the point(s) on the circle which have an \(x\)-value that is twice the \(y\)-value, we substitute \(x = 2y\) into the equation of the circle:
\begin{align*} x^{2} + y^{2} &= 45 \\ (2y)^{2} + y^{2} &= 45 \\ 4y^{2} + y^{2} &= 45 \\ 5y^{2} &= 45 \\ y^{2} &= 9 \\ \therefore y &= \pm 3 \\ \text{If } y = -3: \quad x &= 2(-3) \\ &= -6 \\ \text{If } y = 3: \quad x &= 2(3) \\ &= 6 \end{align*}This gives the points \((6;3)\) and \((-6; -3)\).
Note: we can check that both points lie on the circle by substituting the coordinates into the equation of the circle:
\begin{align*} (6)^2 + (3)^2 &= 36 + 9 = 45 \\ (-6)^2 + (-3)^2 &= 36 + 9 = 45 \end{align*}Complete the following for each circle given below:
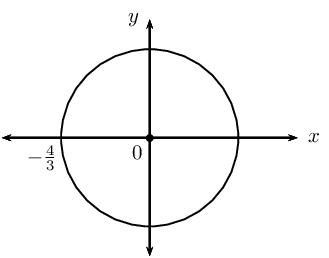
\(x^{2} + y^{2} = 16\)

This gives the points \(\left( 1; \sqrt{15} \right)\) and \(\left( 1; -\sqrt{15} \right)\).
\(x^{2} + y^{2} = 100\)
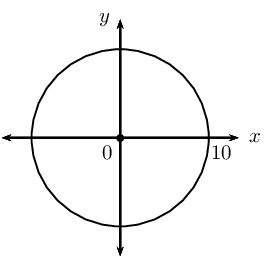
This gives the points \(\left( 2; \sqrt{96} \right)\) and \(\left( 2; -\sqrt{96} \right)\).
\(3x^{2} + 3y^{2} = 27\)
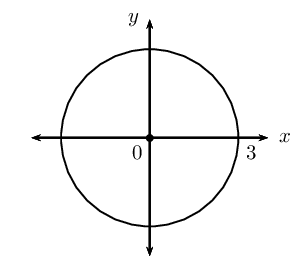
This gives the points \(\left( 1; \sqrt{8} \right)\) and \(\left( 1; -\sqrt{8} \right)\).
\(y^{2} = 20 - x^{2}\)
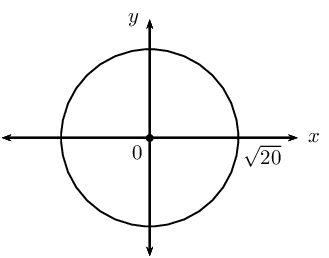
This gives the points \(\left( 2; 4 \right)\) and \(\left( 2; -4 \right)\).
\(x^{2} + y^{2} = \text{2,25}\)
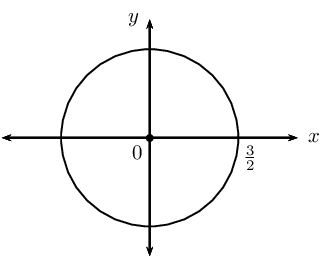
This gives the points \(\left( 1; \frac{\sqrt{5}}{2} \right)\) and \(\left( 1; -\frac{\sqrt{5}}{2} \right)\).
\(y^{2} = - x^{2} + \frac{10}{9}\)
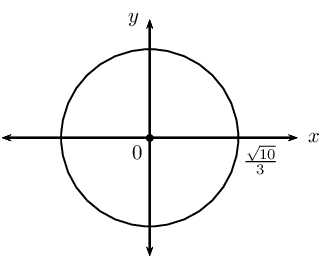
This gives the points \(\left( 1; \frac{1}{3} \right)\) and \(\left( 1; -\frac{1}{3} \right)\).
Determine the equation of the circle:
Determine whether or not the following equations represent a circle:
Determine the value(s) of \(g\) if \(\left( \sqrt{3}; g \right)\) is a point on the circle \(x^{2} + y^{2} = 19\).
This gives the points \(\left( \sqrt{3}; 4 \right)\) and \(\left( \sqrt{3}; -4 \right)\).
\(A(s;t)\) is a point on the circle with centre at the origin and a diameter of \(\text{40}\) \(\text{cm}\).
Therefore, \(A \left( 6 \sqrt{10}; 2\sqrt{10} \right)\) or \(A \left( -6 \sqrt{10}; -2\sqrt{10} \right)\)
Therefore, \(A \left(4 \sqrt{5}; 8\sqrt{5} \right)\) or \(A \left( -4 \sqrt{5}; -8\sqrt{5} \right)\)
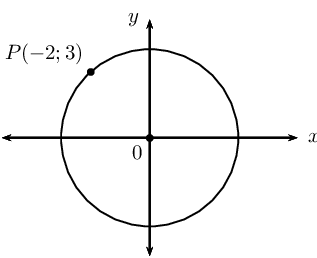
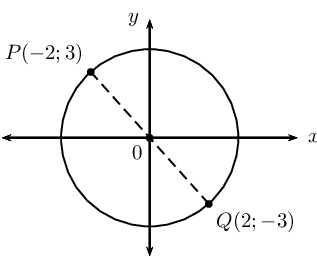
\(P(-2;3)\) lies on a circle with centre at \((0;0)\).
If \(PQ\) is a diameter of the circle, then point \(Q\) must lie opposite point \(P\) on the circumference of the circle. Using symmetry about the origin, the coordinates of point \(Q\) are \((2;-3)\).
Alternative: Use the distance formula
\begin{align*} PQ &= \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^2} \\ &= \sqrt{(-2-2)^{2} + (3-(-3))^2} \\ &= \sqrt{(-4)^{2} + (6)^2} \\ &= \sqrt{16 + 36} \\ &= \sqrt{52} \\ &= \sqrt{4 \cdot 13} \\ &= 2 \sqrt{13} \text{ units} \end{align*}\(PQ\) passes through the origin, therefore \(c = 0\).
For perpendicular line:
\begin{align*} m_{PQ} \times m_{\perp} &= -1 \\ - \frac{3}{2} \times m_{\perp} &= -1 \\ m_{\perp} &= \frac{2}{3} \\ y - y_{1} &= m (x - x_{1}) \\ y - y_{1} &= \frac{2}{3} (x - x_{1}) \\ \text{Substitute } P(-2;3) \quad y - 3 &= \frac{2}{3} (x - (-2)) \\ y - 3 &= \frac{2}{3}x + \frac{4}{3} \\ y &= \frac{2}{3}x + \frac{4}{3} + \frac{9}{3} \\ &= \frac{2}{3}x + \frac{13}{3} \end{align*}Complete the following for each equation in the table below:
The first example has been completed.
| Equation | Vertical shift | Horizontal shift | Combined shift |
| \(y - 3x^{2} = 0\) | \((y - 1) - 3x^{2} = 0\) | \(y - 3(x - 2)^{2} = 0\) | \((y - 1) - 3(x - 2)^{2} = 0\) |
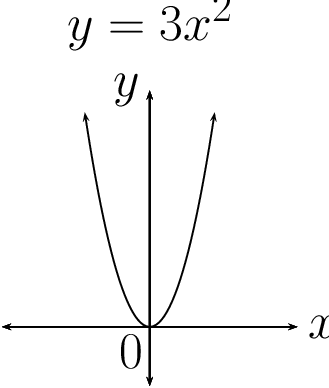 |
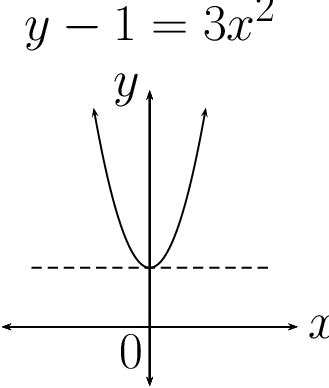 |
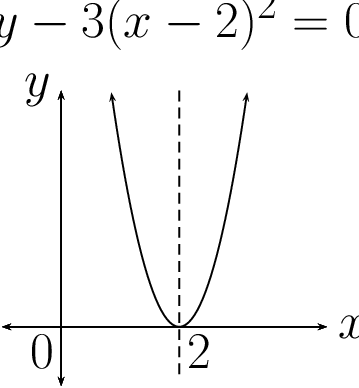 |
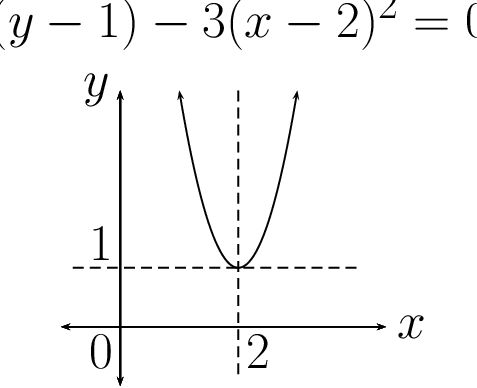 |
| \(y - 5^{x} = 0\) | |||
| \(x^{2} + y^{2} = 4\) | |||
Use the table to answer the following questions:
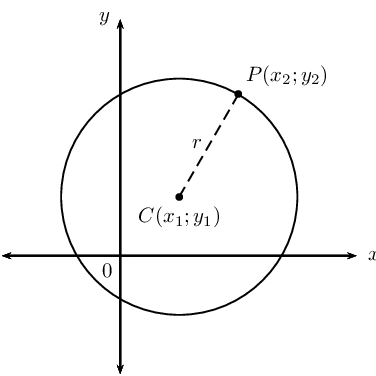
Consider a circle in the Cartesian plane with centre at \(C(x_{1}; y_{1})\) and with a radius of \(r\) units. If \(P(x_{2}; y_{2})\) is any point on the circumference of the circle, we can use the distance formula to calculate the distance between the two points:
\[PC = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^2}\]The distance \(PC\) is equal to the radius (\(r\)) of the circle:
\begin{align*} r &= \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^2} \\ \therefore r^{2} &= (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^2 \end{align*}If the coordinates of the centre of the circle are \((a;b)\), then the equation of a circle not centred on the origin is:
\[(x_{2} - a)^{2} + (y_{2} - b)^2 = r^{2}\]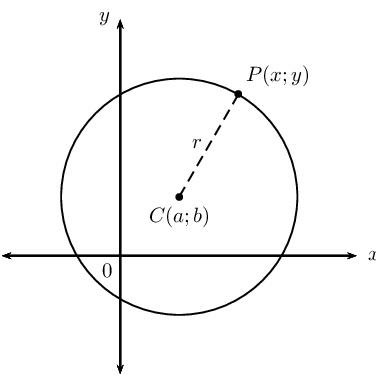
Equation of a circle with centre at \((a;b)\):
If \(P(x;y)\) is a point on a circle with centre \(C(a;b)\) and radius \(r\), then the equation of the circle is:
\[(x - a)^{2} + (y - b)^{2} = r^{2}\]A circle with centre \((0;0)\) is a special case of the general equation:
\[(x - a)^{2} + (y - b)^{2} = r^{2}\] \begin{align*} (x - 0)^{2} + (y - 0)^{2} &= r^{2} \\ \therefore x^{2} + y^{2} &= r^{2} \end{align*}\(F(6;-4)\) is a point on the circle with centre \((3;-4)\).
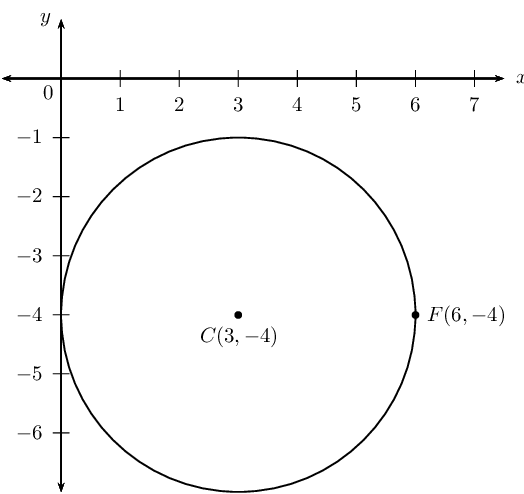
Write down the general equation of a circle with centre \((a;b)\) and substitute the coordinates \((3;-4)\):
\begin{align*} (x - a)^{2} + (y - b)^{2} &= r^{2} \\ (x - 3)^{2} + (y - (-4))^{2} &= r^{2} \\ (x - 3)^{2} + (y + 4)^{2} &= r^{2} \end{align*}Substitute the coordinates of \(F(6;-4)\) to determine the value of \(r^{2}\):
\begin{align*} (6 - 3)^{2} + (-4 + 4)^{2} &= r^{2} \\ (3)^{2} + (0)^{2} &= r^{2} \\ 9 &= r^{2} \\ \therefore (x - 3)^{2} + (y + 4)^{2} &= 9 \end{align*}If \(G \left( \frac{3}{2} ; -2 \right)\) lies on the circle, then it will satisfy the equation of the circle:
\begin{align*} \text{LHS } &= \left( \frac{3}{2} - 3 \right)^{2} + \left( -2 + 4 \right)^{2} \\ &= \left( - \frac{3}{2} \right)^{2} + \left( 2 \right)^{2} \\ &= \frac{9}{4} + 4 \\ &= \frac{9}{4} + \frac{16}{4} \\ &= \frac{25}{4} \end{align*}\begin{align*} \text{RHS } &= 9 \\ \therefore \text{LHS } &\ne \text{ RHS} \end{align*}Therefore \(G\) does not lie on the circle.
To determine the \(y\)-intercept(s), we let \(x = 0\):
\begin{align*} (0 - 3)^{2} + (y + 4)^{2} &= 9 \\ 9 + (y + 4)^{2} &= 9 \\ (y + 4)^{2} &= 0 \\ y + 4 &= 0 \\ \therefore y &= -4 \end{align*}The circle cuts the \(y\)-axis at \((0;-4)\).
Determine the coordinates of the centre of the circle and the length of the radius for \(3x^{2} + 6x + 3y^{2} - 12y - 33 = 0\).
The coefficient of the \(x^{2}\) and \(y^{2}\) term must be \(\text{1}\), so we take out \(\text{3}\) as a common factor:
\[x^{2} + 2x + y^{2} - 4y - 11 = 0\]Take half the coefficient of the \(x\) term, square it; then add and subtract it from the equation.
The coefficient of the \(x\) term is \(\text{2}\), so then \(\left( \frac{2}{2} \right)^{2} = (1)^{2} = 1\).
Take half the coefficient of the \(y\) term, square it; then add and subtract it from the equation.
The coefficient of the \(y\) term is \(-\text{4}\), so then \(\left( \frac{-4}{2} \right)^{2} = (-2)^{2} = 4\).
\begin{align*} x^{2} + 2x + y^{2} - 4y - 11 &= 0 \\ (x^{2} + 2x + 1 ) - 1 + (y^{2} - 4y + 4) -4 - 11 &= 0 \\ \left( x + 1 \right)^{2} + \left( y - 2 \right)^{2} - 16 &= 0 \\ \left( x + 1 \right)^{2} + \left( y - 2 \right)^{2} &= 16 \end{align*}The centre of the circle is \((-1;2)\) and the radius is \(\text{4}\) units.
Given \(S(-3;4)\) and \(T(-3;-4)\) on the Cartesian plane.
For symmetry about the origin, every point \((x; y)\) is symmetrical to \((−x; −y)\). So \(S(-3;4)\) is symmetrical to \(U(3;-4)\) and \(T(-3;-4)\) is symmetrical to \(V(3;4)\).
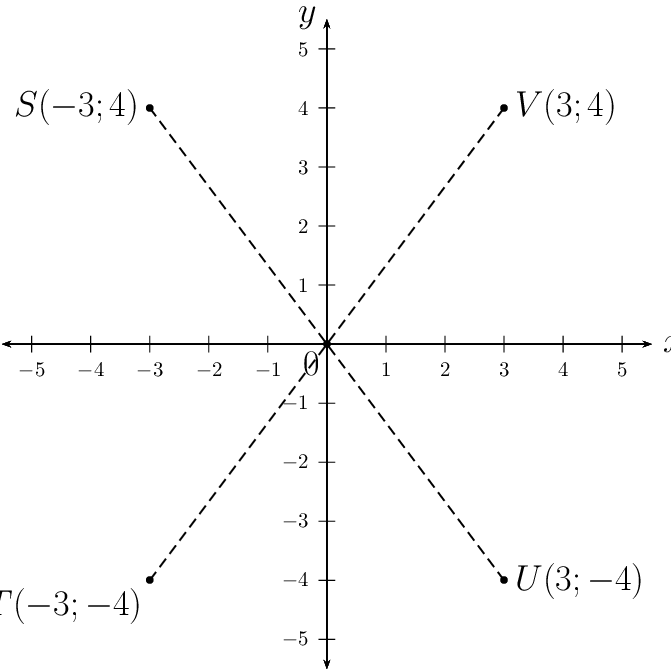
The mid-point of the line \(SU\) is the origin.
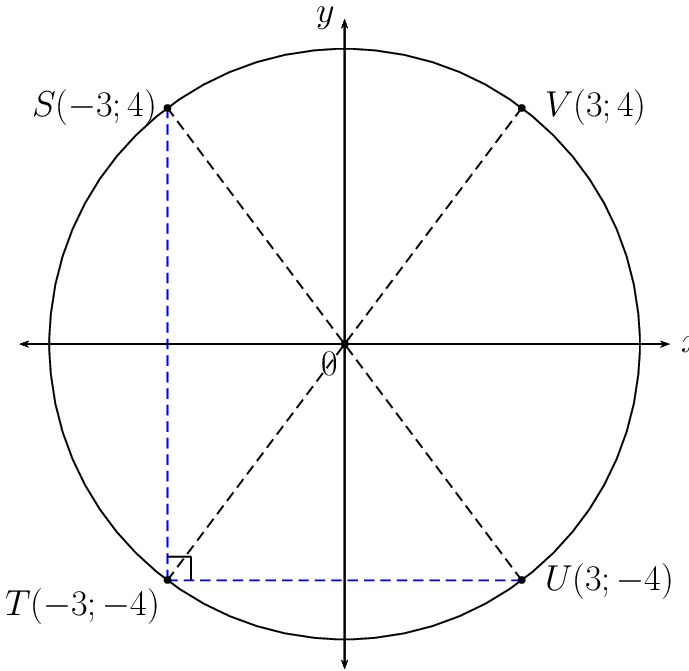
\(SU\) passes through the centre of the circle and is therefore a diameter. From Euclidean geometry, we know that the diameter of the circle subtends a right-angle at the circumference, therefore \(S\hat{T}U = \text{90} °\) (angle in semi-circle).
Determine the gradient of \(SU\):
\begin{align*} m_{SU} &= \frac{y_{S} - y_{U}}{x_{S}- x_{U}} \\ &= \frac{4 - (- 4)}{-3 - 3} \\ &= \frac{8}{-6} \\ &= - \frac{4}{3} \end{align*}Let the gradient of the line perpendicular to \(SU\) be \(m_{P}\):
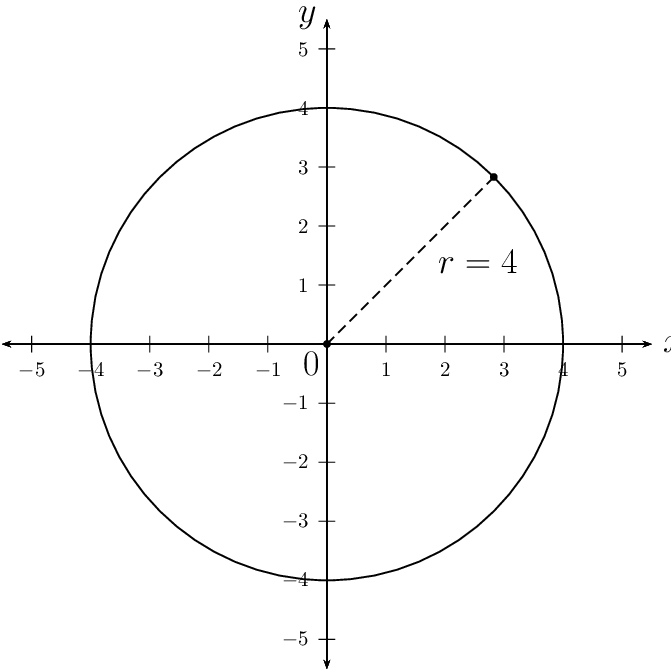
\begin{align*} m_{SU} \times m_{P} &= -1 \\ - \frac{4}{3} \times m_{P} &= -1 \\ \therefore m_{P} &= \frac{3}{4} \\ y - y_{1} &= m(x - x_{1}) \\ \text{Substitute } S(-3;4): \quad y - 4 &= \frac{3}{4} (x - (-3)) \\ y - 4 &= \frac{3}{4} (x + 3) \\ y &= \frac{3}{4}x + \frac{25}{4} \end{align*}Given: a circle with centre \((0;0)\) and a radius of \(\text{4}\) units.
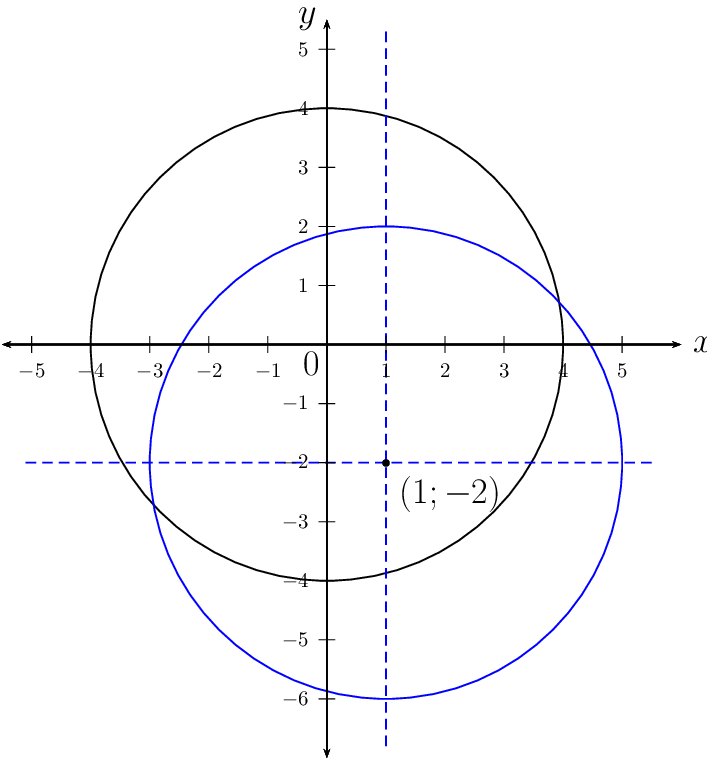
Therefore the equation of the shifted circle is \((x - 1)^{2} + (y + 2)^{2} = 16\) with centre at \((1;-2)\) and radius of \(4\) units.
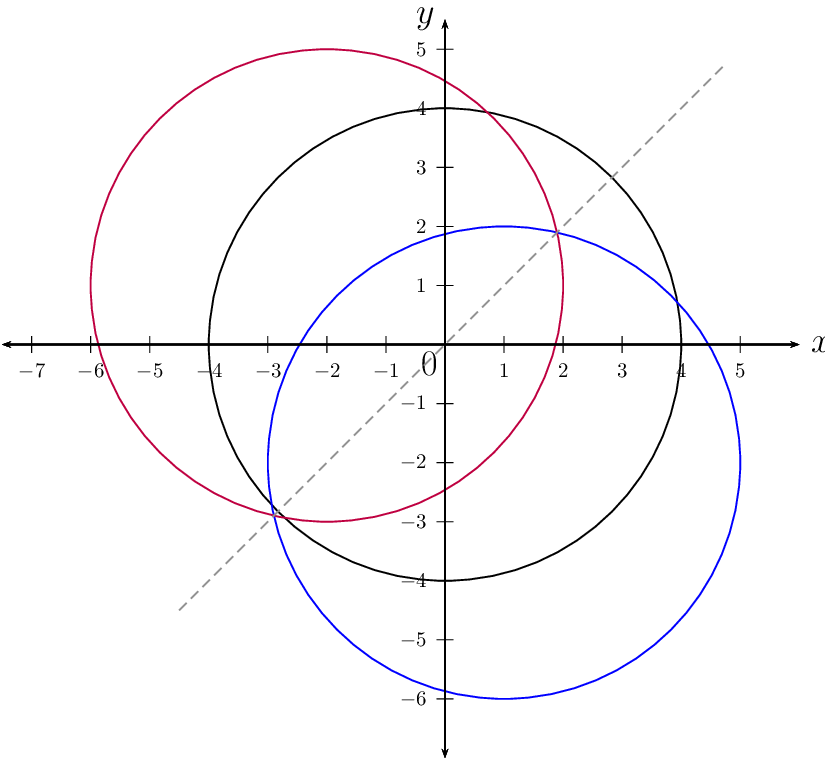
The shifted circle is reflected about the line \(y = x\). The \(x\) and \(y\) variables are interchanged to give the circle with equation \((y - 1)^{2} + (x + 2)^{2} = 16\) and centre at \((-2;1)\).
A circle with centre on the line \(y = -x + 5\) passes through the points \(P(5;8)\) and \(Q(9;4)\). Determine the equation of the circle.
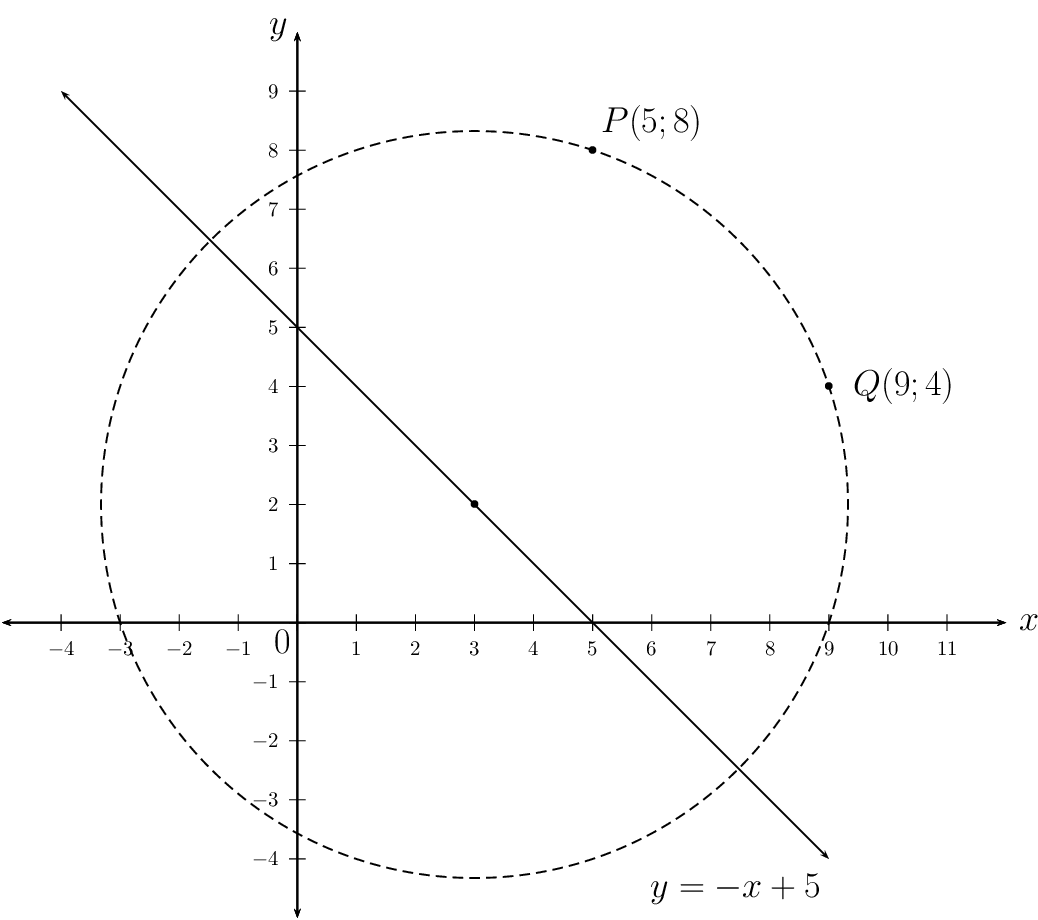
Consider the line \(y = -x + 5\). Any point on this line will have the coordinates \((x; - x + 5)\). Since the centre of the circle lies on the line \(y = -x + 5\), we can write the equation of the circle as
\begin{align*} (x - a)^{2} + (y - (- a + 5))^{2} & = r^{2} \\ (x - a)^{2} + (y + a - 5)^{2} & = r^{2} \end{align*}We need two equations to solve for the two unknown variables. We substitute the two given points, \(P(5;8)\) and \(Q(9;4)\) and solve for \(a\) and \(r\) simultaneously:
\begin{align*} \text{Substitute } P(5;8): \quad (5 - a)^{2} + (8 + a - 5)^{2} & = r^{2} \\ (5 - a)^{2} + (a + 3)^{2} & = r^{2} \\ 25 - 10a + a^{2} + a^{2} + 6a + 9 & = r^{2} \\ 2a^{2} - 4a + 34 & = r^{2} \ldots (1) \\ & \\ \text{Substitute } Q(9;4): \quad (9 - a)^{2} + (4 + a - 5)^{2} & = r^{2} \\ (9 - a)^{2} + (a - 1)^{2} & = r^{2} \\ 81 - 18a + a^{2} + a^{2} - 2a + 1 & = r^{2} \\ 2a^{2} - 20a + 82 & = r^{2} \ldots (2) \\ & \\ (1) - (2): \quad 16a - 48 &= 0 \\ 16a &= 48 \\ \therefore a &= 3 \\ \text{Substitute into } (2): \quad r^{2} &= 2(3)^{2} - 20 (3) + 82 \\ &= 18 - 60 + 82 \\ &= 40 \\ \text{And } \quad b &= -a + 5 \\ &= -3 + 5 \\ &= 2 \end{align*}The equation of the circle is \((x - 3)^{2} + (y - 2)^{2} = 40\).
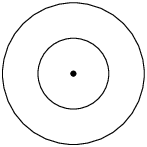 |
Circles with the same centre. |
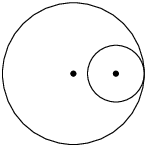 |
Circles touch internally at one point: the distance between the centres is equal to the difference between the radii. \(d = r_{2} - r_{1}\) |
 |
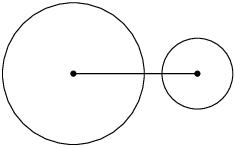
Circles intersect at two points: the distance between the centres is less than the sum of the radii. \(d < r_{1} + r_{2}\) |
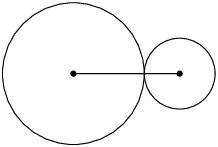 |
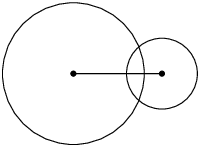
Circles touch externally at one point: the distance between the centres is equal to the sum of the radii. \(d = r_{1} + r_{2}\) |
 |
Circles do not touch or intersect: the distance between the centres is greater than the sum of the radii. \(d > r_{1} + r_{2}\) |
Determine whether or not each of the following equations represents a circle. If not, give a reason.
Write down the equation of the circle:
Determine the centre and the length of the radius for the following circles:
Centre: \((0;2)\), \(r = 5\) units
Centre: \(\left(-\frac{1}{2}; 0 \right)\), \(r = 2\) units
Centre: \((2;-1)\), \(r = \sqrt{10}\) units
Centre: \((-1;3)\), \(r = 5\) units
Centre: \((-3;-4 )\), \(r = \sqrt{30}\) units
Centre: \(\left( \frac{1}{3}; 2\right)\), \(r = \sqrt{8}\) units
Centre: \((-4;5 )\), \(r = \sqrt{20}\) units
Centre: \((3;-3)\), \(r = \sqrt{12}\) units
A circle cuts the \(x\)-axis at \(R(-2;0)\) and \(S(2;0)\). If \(r = \sqrt{20}\) units, determine the possible equation(s) of the circle. Draw a sketch.
The equation of the circle passing through points \(R\) and \(S\) is \(x^{2} + (y + 4)^{2} = 20\) or \(x^{2} + (y - 4)^{2} = 20\).
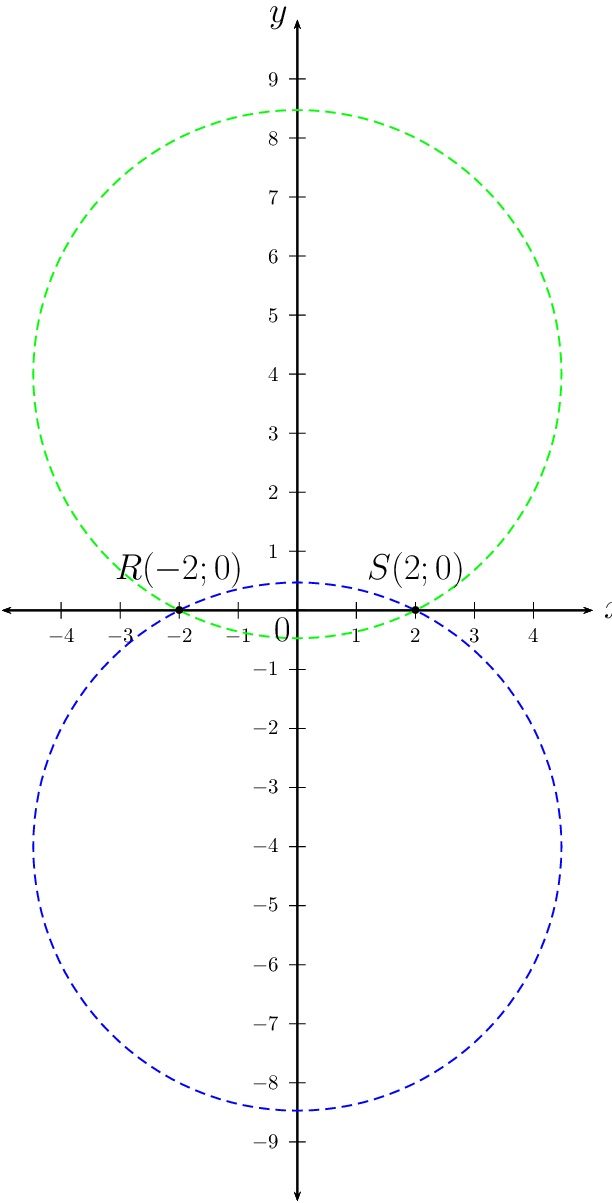
\(P(1;2)\) and \(Q(-5;-6)\) are points on a circle such that \(PQ\) is a diameter. Determine the equation of the circle.
Use the distance formula to determine the length of the diameter.
\begin{align*} PQ &= \sqrt{ (x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} } \\ &= \sqrt{ (- 5 - 1)^{2} + (-6 - 2)^{2} } \\ &= \sqrt{ (- 6)^{2} + (-8)^{2} } \\ &= \sqrt{36 +64} \\ &= \sqrt{100} \\ &= 10 \\ \text{And } r &= \frac{1}{2} \times \text{ diameter} \\ &= \frac{1}{2} \times 10 \\ &= 5 \\ (x - a)^{2} + (y - b)^{2} &= (5)^{2} \\ (x - a)^{2} + (y - b)^{2} &= 25 \end{align*}Given \(PQ\) is a diameter of the circle, then the centre is the mid-point of PG:
\begin{align*} M(x;y) &= \left( \frac{x_{1} + x_{2}}{2}; \frac{y_{1} + y_{2}}{2} \right) \\ &= \left( \frac{1 - 5}{2}; \frac{2 - 6}{2} \right) \\ &= \left( \frac{-4}{2}; \frac{-4}{2} \right) \\ &= \left(-2; -2 \right) \end{align*}Therefore the centre is \((-2;-2)\) and the equation of the circle is \((x + 2)^{2} + (y + 2)^{2} = 25\).
A circle with centre \(N(4;4)\) passes through the points \(K(1;6)\) and \(L(6;7)\).
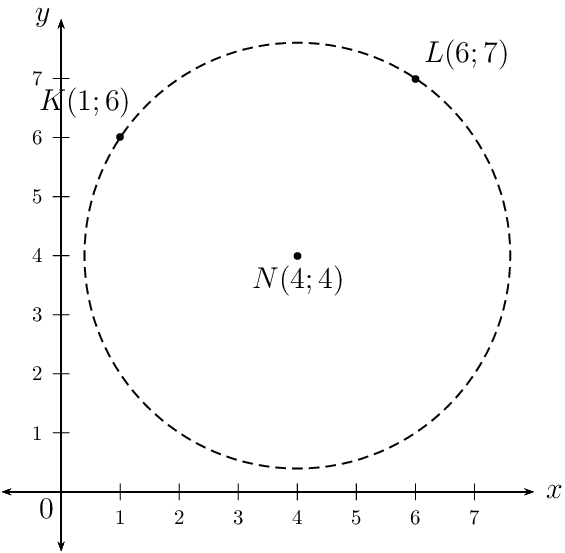
The equation of the circle is \((x - 4)^{2} + (y - 4)^{2} = 13\) .
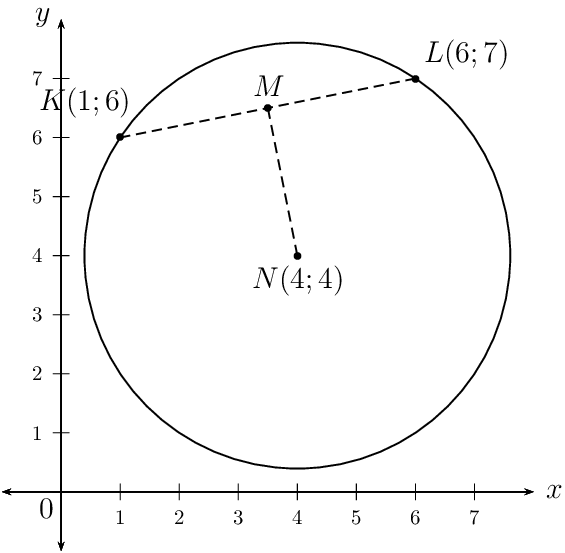
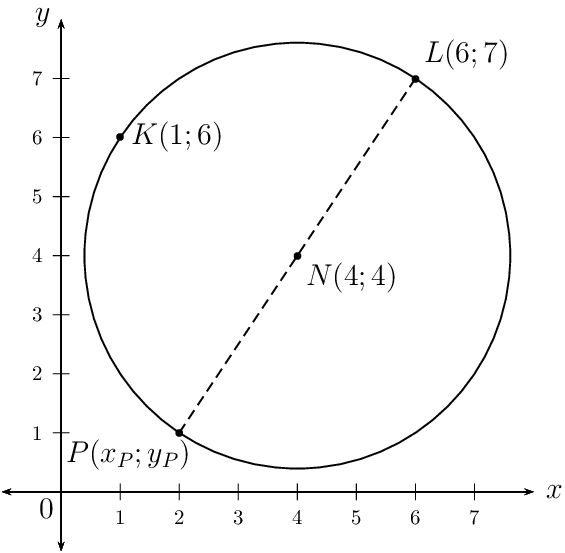
Use the mid-point formula to calculate the coordinates of \(P\):
\begin{align*} (x;y) = \left( \frac{x_{1} + x_{2}}{2}; \frac{y_{1} + y_{2}}{2} \right) \\ N(4;4) = \left( \frac{x_{P} + 6}{2}; \frac{y_{P} + 7}{2} \right) \\ \therefore 4 &= \frac{x_{P} + 6}{2} \\ 8 &= x_{P} + 6 \\ x_{P} &= 2 \\ \text{And } 4 &= \frac{y_{P} + 7}{2} \\ 8 &= y_{P} + 7\\ y_{P} &= 1 \\ \therefore & P(2;1) \end{align*}Given that the centre of the circle lies on the line \(y = 2x - 5\), we can write the coordinates of the circle as \((p; 2p - 5)\) and the equation of the circle becomes:
\begin{align*} (x - a)^{2} + (y - b)^{2} &= r^{2} \\ (x - p)^{2} + (y - (2p - 5))^{2} &= r^{2} \\ (x - p)^{2} + (y - 2p + 5)^{2} &= r^{2} \\ \text{Substitute } A(7;4): \quad (7 - p)^{2} + (-4 - 2p + 5)^{2} &= r^{2} \\ (7 - p)^{2} + (1 - 2p)^{2} &= r^{2} \\ 49 - 14p + p^{2} + 1 -4p + 4p^{2} &= r^{2} \\ 5p^{2} - 18p + 50 &= r^{2} \ldots (1) \\ \text{Substitute } B(-5;-2): \quad (-5 - p)^{2} + (-2 - 2p + 5)^{2} &= r^{2} \\ (-5 - p)^{2} + (3 - 2p)^{2} &= r^{2} \\ 25 + 10p + p^{2} + 9 - 12p + 4p^{2} &= r^{2} \\ 5p^{2} - 2p + 34 &= r^{2} \ldots (2) \\ (1) - (2): \quad -16p + 16 &= 0 \\ -16p &= -16 \\ \therefore p = x &= 1 \\ \text{And } y &= 2(1) - 5 \\ &= -3 \\ \text{And } r^{2} &= 5(1)^{2} - 2(1) + 34 \\ &= 5 - 2 + 34 \\ \therefore r^{2} &= 37 \end{align*}The equation of the circle is \((x - 1)^{2} + (y + 3)^{2} = 37\).
A circle with centre \((0;0)\) passes through the point \(T(3;5)\).

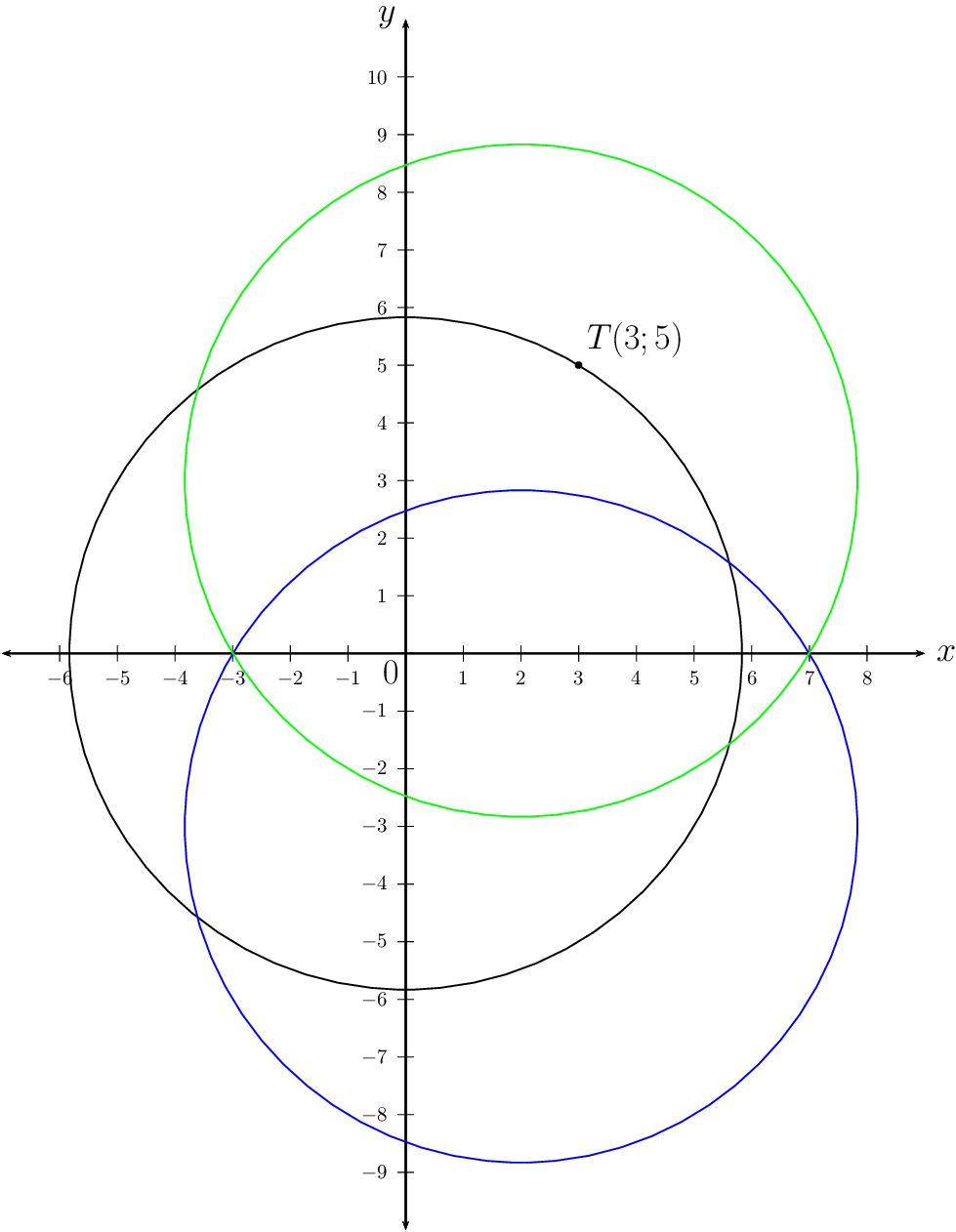
Centre of the shifted circle: \((2;3)\)
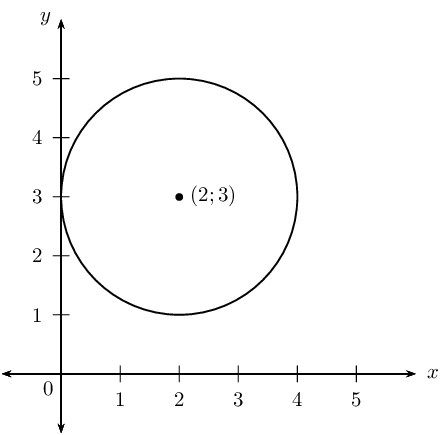
Determine whether the circle \(x^{2} - 4x + y^{2} - 6y + 9 = 0\) cuts, touches or does not intersect the \(x\)-axis and the \(y\)-axis.
The radius of the circle is \(\text{2}\) units. The distance from the centre to the \(y\)-axis is \(\text{2}\) units, therefore the circle will touch the \(y\)-axis. The distance from the centre to the \(x\)-axis is \(\text{3}\) units, therefore the circle will not intersect with the \(x\)-axis.
|
Previous
7.1 Revision
|
Table of Contents |
Next
7.3 Equation of a tangent to a circle
|