|
Previous
11.2 Histograms
|
Next
11.4 Variance and standard deviation
|
Cumulative histograms, also known as ogives, are graphs that can be used to determine how many data values lie above or below a particular value in a data set. The cumulative frequency is calculated from a frequency table, by adding each frequency to the total of the frequencies of all data values before it in the data set. The last value for the cumulative frequency will always be equal to the total number of data values, since all frequencies will already have been added to the previous total.
An ogive is drawn by
Determine the cumulative frequencies of the following grouped data and complete the table below. Use the table to draw an ogive of the data.
| Interval | Frequency | Cumulative frequency |
| \(10 < n \le 20\) | \(\text{5}\) | |
| \(20 < n \le 30\) | \(\text{7}\) | |
| \(30 < n \le 40\) | \(\text{12}\) | |
| \(40 < n \le 50\) | \(\text{10}\) | |
| \(50 < n \le 60\) | \(\text{6}\) |
To determine the cumulative frequency, we add up the frequencies going down the table. The first cumulative frequency is just the same as the frequency, because we are adding it to zero. The final cumulative frequency is always equal to the sum of all the frequencies. This gives the following table:
| Interval | Frequency | Cumulative frequency |
| \(10 < n \le 20\) | \(\text{5}\) | \(\text{5}\) |
| \(20 < n \le 30\) | \(\text{7}\) | \(\text{12}\) |
| \(30 < n \le 40\) | \(\text{12}\) | \(\text{24}\) |
| \(40 < n \le 50\) | \(\text{10}\) | \(\text{34}\) |
| \(50 < n \le 60\) | \(\text{6}\) | \(\text{40}\) |
The first coordinate in the plot always starts at a \(y\)-value of \(\text{0}\) because we always start from a count of zero. So, the first coordinate is at \((10;0)\) — at the beginning of the first interval. The second coordinate is at the end of the first interval (which is also the beginning of the second interval) and at the first cumulative count, so \((20;5)\). The third coordinate is at the end of the second interval and at the second cumulative count, namely \((30;12)\), and so on.
Computing all the coordinates and connecting them with straight lines gives the following ogive.
Ogives do look similar to frequency polygons, which we saw earlier. The most important difference between them is that an ogive is a plot of cumulative values, whereas a frequency polygon is a plot of the values themselves. So, to get from a frequency polygon to an ogive, we would add up the counts as we move from left to right in the graph.
Ogives are useful for determining the median, percentiles and five number summary of data. Remember that the median is simply the value in the middle when we order the data. A quartile is simply a quarter of the way from the beginning or the end of an ordered data set. With an ogive we already know how many data values are above or below a certain point, so it is easy to find the middle or a quarter of the data set.
Use the following ogive to compute the five number summary of the data. Remember that the five number summary consists of the minimum, all the quartiles (including the median) and the maximum.
The minimum value in the data set is \(\text{1}\) since this is where the ogive starts on the horizontal axis. The maximum value in the data set is \(\text{10}\) since this is where the ogive stops on the horizontal axis.
The quartiles are the values that are \(\frac{1}{4}\), \(\frac{1}{2}\) and \(\frac{3}{4}\) of the way into the ordered data set. Here the counts go up to \(\text{40}\), so we can find the quartiles by looking at the values corresponding to counts of \(\text{10}\), \(\text{20}\) and \(\text{30}\). On the ogive a count of
The five number summary is \((1; 3; 7; 8; 10)\). The box-and-whisker plot of this data set is given below.
Use the ogive to answer the questions below.
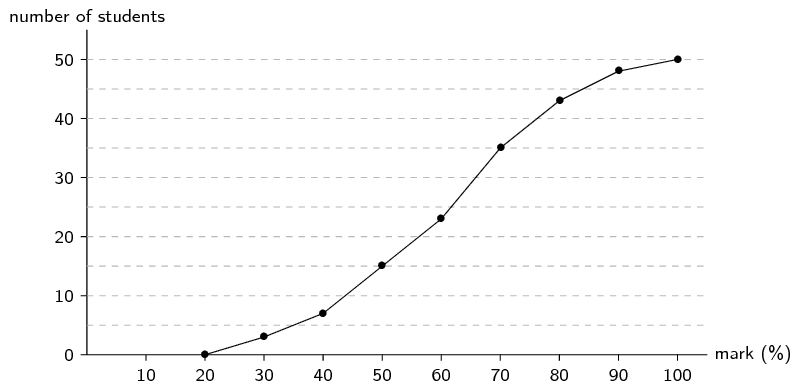
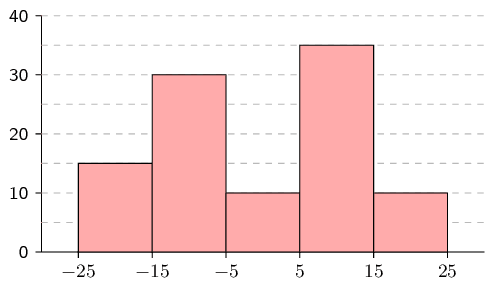
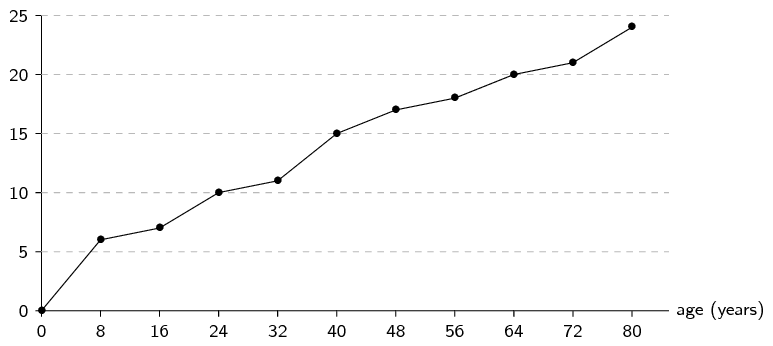
How many students got between \(\text{50}\%\) and \(\text{70}\%\)?
The cumulative plot shows that \(\text{15}\) students got below \(\text{50}\%\) and \(\text{35}\) students got below \(\text{70}\%\). Therefore \(35-15=\text{20}\) students got between \(\text{50}\%\) and \(\text{70}\%\).
How many students got at least \(\text{70}\%\)?
The cumulative plot shows that \(\text{35}\) students got below \(\text{70}\%\) and that there are \(\text{50}\) students in total. Therefore \(50-35=\text{15}\) students got at least (greater than or equal to) \(\text{70}\%\).
To compute the average, we first need to use the ogive to determine the frequency of each interval. The frequency of an interval is the difference between the cumulative counts at the top and bottom of the interval on the ogive. It might be difficult to read the exact cumulative count for some of the points on the ogive. But since the final answer will be rounded to the nearest integer, small errors in the counts will not make a difference. The table below summarises the counts.
| Interval | \([20,30)\) | \([30,40)\) | \([40,50)\) | \([50,60)\) | \([60,70)\) | \([70,80)\) | \([80,90)\) | \([90,100)\) |
| Count | \(\text{3}\) | \(\text{4}\) | \(\text{8}\) | \(\text{8}\) | \(\text{12}\) | \(\text{8}\) | \(\text{5}\) | \(\text{2}\) |
The average is then the centre of each interval, weighted by the count in that interval. \[\frac{3 \times 25 + 4 \times 35 + 8 \times 45 + 8 \times 55 + 12 \times 65 + 8 \times 75 + 5 \times 85 + 2 \times 95}{3+4+8+8+12+8+5+2} = \text{60,2}\] The average mark, rounded to the nearest integer, is \(\text{60}\%\).
Draw the histogram corresponding to this ogive.
To draw the histogram we need to determine the count in each interval.
Firstly, we can find the intervals by looking where the points are plotted on the ogive. Since the points are at \(x\)-coordinates of \(-\text{25}\); \(-\text{15}\); \(-\text{5}\); \(\text{5}\); \(\text{15}\) and \(\text{25}\), it means that the intervals are \([-25;-15)\), etc.
To get the count in each interval we subtract the cumulative count at the start of the interval from the cumulative count at the end of the interval.
| Interval | \([-25;-15)\) | \([-15;-5)\) | \([-5;5)\) | \([5;15)\) | \([15;25)\) |
| Count | \(\text{15}\) | \(\text{30}\) | \(\text{10}\) | \(\text{35}\) | \(\text{10}\) |
From these counts we can draw the following histogram:
The following data set lists the ages of \(\text{24}\) people.
\(\text{2}\); \(\text{5}\); \(\text{1}\); \(\text{76}\); \(\text{34}\); \(\text{23}\); \(\text{65}\); \(\text{22}\); \(\text{63}\); \(\text{45}\); \(\text{53}\); \(\text{38}\)
\(\text{4}\); \(\text{28}\); \(\text{5}\); \(\text{73}\); \(\text{79}\); \(\text{17}\); \(\text{15}\); \(\text{5}\); \(\text{34}\); \(\text{37}\); \(\text{45}\); \(\text{56}\)
Use the data to answer the following questions.
Using an interval width of \(\text{8}\) construct a cumulative frequency plot.
The table below shows the number of people in each age bracket of width \(\text{8}\).
| Interval | \([0;8)\) | \([8;16)\) | \([16;24)\) | \([24;32)\) | \([32;40)\) |
| Count | \(\text{6}\) | \(\text{1}\) | \(\text{3}\) | \(\text{1}\) | \(\text{4}\) |
| Cumulative | \(\text{6}\) | \(\text{7}\) | \(\text{10}\) | \(\text{11}\) | \(\text{15}\) |
| Interval | \([40;48)\) | \([48;56)\) | \([56;64)\) | \([64;72)\) | \([72;80)\) |
| Count | \(\text{2}\) | \(\text{1}\) | \(\text{2}\) | \(\text{1}\) | \(\text{3}\) |
| Cumulative | \(\text{17}\) | \(\text{18}\) | \(\text{20}\) | \(\text{21}\) | \(\text{24}\) |
From this table we can draw the cumulative frequency plot:
How many are below \(\text{30}\)?
How many are below \(\text{60}\)?
Giving an explanation, state below what value the bottom \(\text{50}\%\) of the ages fall.
This question is asking for the median of the data set. The median is, by definition, the value below which \(\text{50}\%\) of the data lie. Since there are \(\text{24}\) values, the median lies between the middle two values, giving \(\text{34}\).
Below what value do the bottom \(\text{40}\%\) fall?
There are \(\text{24}\) values. By drawing a number line, as we do for determining quartiles, we can see that the \(\text{40}\%\) point is between the tenth and eleventh values. The tenth value is \(\text{23}\) and the eleventh value is \(\text{28}\). Therefore \(\text{40}\%\) of the values lie below \(\dfrac{23+28}{2} = \text{25,5}\).
Construct a frequency polygon.
We already have all the values needed to construct the frequency polygon in the table of values above.
The weights of bags of sand in grams is given below (rounded to the nearest tenth):
\(\text{50,1}\); \(\text{40,4}\); \(\text{48,5}\); \(\text{29,4}\); \(\text{50,2}\); \(\text{55,3}\); \(\text{58,1}\); \(\text{35,3}\); \(\text{54,2}\); \(\text{43,5}\)
\(\text{60,1}\); \(\text{43,9}\); \(\text{45,3}\); \(\text{49,2}\); \(\text{36,6}\); \(\text{31,5}\); \(\text{63,1}\); \(\text{49,3}\); \(\text{43,4}\); \(\text{54,1}\)
Learner-dependent answer.
Learner-dependent answer.
Learner-dependent answer.
Learner-dependent answer.
Below what value do \(\text{53}\%\) of the cases fall?
Below what value of \(\text{60}\%\) of the cases fall?
|
Previous
11.2 Histograms
|
Table of Contents |
Next
11.4 Variance and standard deviation
|
