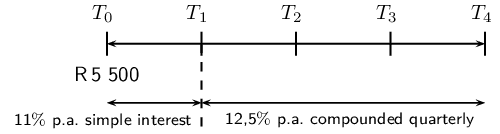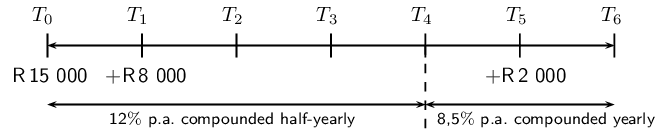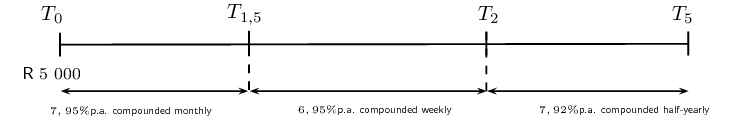Interest can be compounded more than once a year. For example, an investment can be compounded
monthly or quarterly. Below is a table of compounding terms and their corresponding numeric
value (\(p\)). When amounts are compounded more than once per annum, we multiply the number of
years by \(p\) and we also divide the interest rate by \(p\).
Worked example 12: Timelines
\(\text{R}\,\text{5 500}\) is invested for a period of \(\text{4}\) years in a
savings account. For the first year, the investment grows at a simple interest
rate of \(\text{11}\%\) p.a. and then at a rate of \(\text{12,5}\%\) p.a.
compounded quarterly for the rest of the period. Determine the value of the
investment at the end of the \(\text{4}\) years.
Draw a timeline and write down known variables
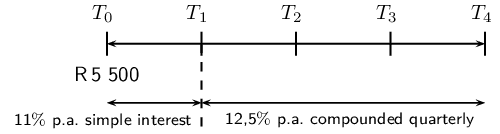
In the timeline above, the intervals are given in years. For example, \(T_0\) is the
start of the investment, \(T_1\) is the end of the first year and \(T_4\) is the
end of the fourth year.
Use the simple interest formula to calculate \(A\) at \(T_1\)
\begin{align*}
A &= P(1 + in) \\
&= \text{5 500}(1 + \text{0,11}) \\
&= \text{R}\,\text{6 105}
\end{align*}
Use the compound interest formula to calculate \(A\) at \(T_4\)
The investment is compounded quarterly, therefore:
\begin{align*}
n &= 3 \times 4 \\
&= 12 \\
\text{and } i &= \frac{\text{0,125}}{4}
\end{align*}
Also notice that the accumulated amount at the end of the first year becomes the
principal amount at the beginning of the second year.
\begin{align*}
A &= P(1 + i)^n \\
&= \text{6 105} \left( 1 + \frac{\text{0,125}}{4} \right)^{12} \\
&= \text{R}\,\text{8 831,88}
\end{align*}
Write the final answer
The value of the investment at the end of the \(\text{4}\) years is
\(\text{R}\,\text{8 831,88}\).
Worked example 13: Timelines
\(\text{R}\,\text{150 000}\) is deposited in an investment account for a period of
\(\text{6}\) years at an interest rate of \(\text{12}\%\) p.a. compounded
half-yearly for the first \(\text{4}\) years and then \(\text{8,5}\%\) p.a.
compounded yearly for the rest of the period. A deposit of \(\text{R}\,\text{8
000}\) is made into the account after the first year and then another deposit of
\(\text{R}\,\text{2 000}\) is made \(\text{5}\) years after the initial
investment. Calculate the value of the investment at the end of the \(\text{6}\)
years.
Draw a timeline and write down known variables
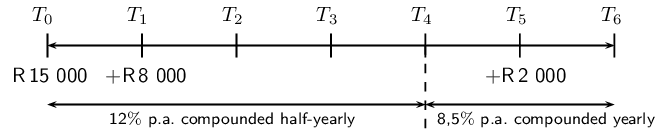
Remember to show when the additional deposits of \(\text{R}\,\text{8 000}\) and
\(\text{R}\,\text{2 000}\) where made into the account. It is very important to
note that the interest rate changes at \(T_4\).
We break this question down into parts and consider each amount separately.
The initial deposit at \(T_0\)
Between \(T_0\) and \(T_4\):
We notice that interest for the first \(\text{4}\) years is compounded half-yearly,
therefore:
\begin{align*}
n_1 &= 4 \times 2 \\
&= 8 \\
\text{and } i_1 &= \frac{\text{0,12}}{2}
\end{align*}
Between \(T_4\) and \(T_6\):
\begin{align*}
n_2 &= 2 \\
\text{and } i_2 &= \text{0,085}
\end{align*}
Therefore the total growth of the initial deposit over the \(\text{6}\) years is:
\begin{align*}
A &= P(1 + i_1)^{n_1}(1 + i_2)^{n_2} \\
&= \text{150 000} \left( 1 + \frac{\text{0,12}}{2} \right)^8 \left(1 +
\text{0,085}\right)^2
\end{align*}
The deposit at \(T_1\)
Between \(T_1\) and \(T_4\):
Interest on this deposit is compounded half-yearly for \(\text{3}\) years, therefore:
\begin{align*}
n_3 &= 3 \times 2 \\
&= 6 \\
\text{and } i_3 &= \frac{\text{0,12}}{2}
\end{align*}
Between \(T_4\) and \(T_6\):
\begin{align*}
n_4 &= 2 \\
\text{and } i_4 &= \text{0,085}
\end{align*}
Therefore the total growth of the deposit over the \(\text{5}\) years is:
\begin{align*}
A &= P(1 + i_3)^{n_3}(1 + i_4)^{n_4} \\
&= \text{8 000} \left(1 + \frac{\text{0,12}}{2} \right)^6 \left(1 +
\text{0,085}\right)^2
\end{align*}
The deposit at \(T_5\)
Accumulate interest for only \(\text{1}\) year:
\begin{align*}
A &= P(1 + i)^n \\
&= \text{2 000}(1 + \text{0,085})^1
\end{align*}
Determine the total calculation
To get as accurate an answer as possible, we do the the calculation on the calculator
in one step. Using the memory and answer recall function on the calculator, we
avoid rounding off until we get the final answer.
\begin{align*}
A &= \text{150 000} \left( 1 + \frac{\text{0,12}}{2} \right)^8 (1 +
\text{0,085})^2 + \text{8 000} \left( 1 + \frac{\text{0,12}}{2} \right)^6 (1 +
\text{0,085})^2 + \text{2 000}(1 + \text{0,085})^1 \\
&= \text{R}\,\text{296 977,00}
\end{align*}
Write the final answer
The value of the investment at the end of the \(\text{6}\) years is
\(\text{R}\,\text{296 977,00}\).
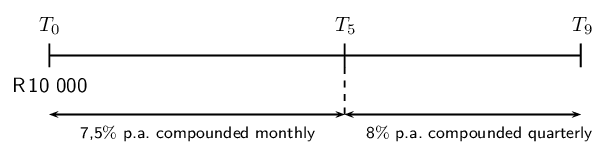
Worked example 14: Timelines
\(\text{R}\,\text{60 000}\) is invested in an account which offers interest at
\(\text{7}\%\) p.a. compounded quarterly for the first \(\text{18}\) months.
Thereafter the interest rate changes to \(\text{5}\%\) p.a. compounded monthly.
Three years after the initial investment, \(\text{R}\,\text{5 000}\) is
withdrawn from the account. How much will be in the account at the end of
\(\text{5}\) years?
Draw a timeline and write down known variables
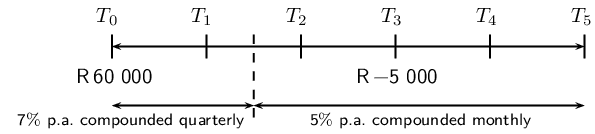
Remember to show when the withdrawal of \(\text{R}\,\text{5 000}\) was taken out of
the account. It is also important to note that the interest rate changes after
\(\text{18}\) months (\(T_{1\frac{1}{2}}\)).
We break this question down into parts and consider each amount separately.
The initial deposit at \(T_0\)
Interest for the first \(\text{1,5}\) years is compounded quarterly, therefore:
\begin{align*}
n_1 &= \text{1,5} \times 4 \\
&= 6 \\
\text{and } i_1 &= \frac{\text{0,07}}{4}
\end{align*}
Interest for the remaining \(\text{3,5}\) years is compounded monthly, therefore:
\begin{align*}
n_2 &= \text{3,5} \times 12 \\
&= 42 \\
\text{and } i_2 &= \frac{\text{0,05}}{12}
\end{align*}
Therefore the total growth of the initial deposit over the \(\text{5}\) years is:
\begin{align*}
A &= P(1 + i_1)^{n_1} (1 + i_2)^{n_2} \\
&= \text{60 000} \left( 1 + \frac{\text{0,07}}{4} \right)^6 \left(1 +
\frac{\text{0,05}}{12} \right)^{42}
\end{align*}
The withdrawal at \(T_3\)
We calculate the interest that the \(\text{R}\,\text{5 000}\) would have earned if it
had remained in the account:
\begin{align*}
n &= 2 \times 12 \\
&= 24 \\
\text{and } i &= \frac{\text{0,05}}{12}
\end{align*}
Therefore we have that:
\begin{align*}
A &= P(1 + i)^n \\
&= \text{5 000} \left(1 + \frac{\text{0,05}}{12} \right)^{24}
\end{align*}
Determine the total calculation
We subtract the withdrawal and the interest it would have earned from the accumulated
amount at the end of the \(\text{5}\) years:
\begin{align*}
A &= \text{60 000} \left( 1 + \frac{\text{0,07}}{4} \right)^6 \left(1 +
\frac{\text{0,05}}{12}\right)^{42} - \text{5 000} \left(1 + \frac{\text{0,05}}{12}
\right)^{24} \\
&= \text{R}\,\text{73 762,19}
\end{align*}
Write the final answer
The value of the investment at the end of the \(\text{5}\) years is
\(\text{R}\,\text{73 762,19}\).