1.2 Rational exponents and surds | Exponents and surds

1.2 Rational exponents and surds (EMBF5)

The laws of exponents can also be extended to include the rational numbers. A rational number is any number that can be written as a fraction with an integer in the numerator and in the denominator. We also have the following definitions for working with rational exponents.

If \(r^n = a\), then \(r = \sqrt[n]{a} \quad (n \geq 2)\)
\(a^{\frac{1}{n}} = \sqrt[n]{a}\)
\(a^{-\frac{1}{n}} = (a^{-1})^{\frac{1}{n}} = \sqrt[n]{\frac{1}{a}}\)
\(a^{\frac{m}{n}} = (a^{m})^{\frac{1}{n}} = \sqrt[n]{a^m}\)

where \(a > 0\), \(r > 0\) and \(m,n \in \mathbb{Z}\), \(n \ne 0\).

For \(\sqrt{25} = 5\), we say that \(\text{5}\) is the square root of \(\text{25}\) and for \(\sqrt[3]{8} = 2\), we say that \(\text{2}\) is the cube root of \(\text{8}\). For \(\sqrt[5]{32} = 2\), we say that \(\text{2}\) is the fifth root of \(\text{32}\).

When dealing with exponents, a root refers to a number that is repeatedly multiplied by itself a certain number of times to get another number. A radical refers to a number written as shown below.

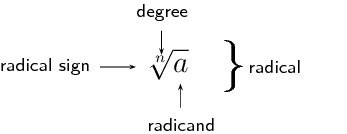
The radical symbol and degree show which root is being determined. The radicand is the number under the radical symbol.

If \(n\) is an even natural number, then the radicand must be positive, otherwise the roots are not real. For example, \(\sqrt[4]{16} = 2\) since \(2 \times 2 \times 2 \times 2 = 16\), but the roots of \(\sqrt[4]{-16}\) are not real since \((-2) \times (-2) \times (-2) \times (-2) \ne -16\).
If \(n\) is an odd natural number, then the radicand can be positive or negative. For example, \(\sqrt[3]{27} = 3\) since \(3 \times 3 \times 3 = 27\) and we can also determine \(\sqrt[3]{-27} = -3\) since \((-3) \times (-3) \times (-3) = -27\).

A surd is a radical which results in an irrational number. Irrational numbers are numbers that cannot be written as a fraction with the numerator and the denominator as integers. For example, \(\sqrt{12}\), \(\sqrt[3]{\text{100}}\), \(\sqrt[5]{25}\) are surds.

Worked example 3: Rational exponents

Write each of the following as a radical and simplify where possible:

\(18^\frac{1}{2}\)
\((-\text{125})^{-\frac{1}{3}}\)
\(4^\frac{3}{2}\)
\((-81)^\frac{1}{2}\)
\((\text{0,008})^\frac{1}{3}\)

\(18^\frac{1}{2} = \sqrt{18}\)
\((-\text{125})^{-\frac{1}{3}} = \sqrt[3]{(-\text{125})^{-1}} = \sqrt[3]{\dfrac{1}{-\text{125}}} = \sqrt[3]{\dfrac{1}{(-5)^3}} = -\dfrac{1}{5}\)
\(4^\frac{3}{2} = (4^3)^{\frac{1}{2}} = \sqrt{4^3} = \sqrt{64} = 8\)
\((-81)^\frac{1}{2} = \sqrt{-81} =\) not real
\((\text{0,008})^\frac{1}{3} = \sqrt[3]{\dfrac{8}{\text{1 000}}} = \sqrt[3]{\dfrac{2^3}{10^3}} = \frac{2}{10} = \dfrac{1}{5}\)

temp text

Video: 223M

Worked example 4: Rational exponents

Simplify without using a calculator:

\[\left(\frac{5}{4^{-1}-9^{-1}}\right)^{\frac{1}{2}}\]

Write the fraction with positive exponents in the denominator

\[\left( \dfrac{5}{\frac{1}{4} - \frac{1}{9}} \right)^{\frac{1}{2}}\]

Simplify the denominator

\begin{align*} &= \left( \dfrac{5}{\frac{9-4}{36}} \right)^{\frac{1}{2}} \\ &= \left( \dfrac{5}{\frac{5}{36}} \right)^{\frac{1}{2}} \\ &= \left( 5 \div \frac{5}{36} \right)^{\frac{1}{2}} \\ &= \left( 5 \times \frac{36}{5} \right)^{\frac{1}{2}} \\ &= (36)^{\frac{1}{2}} \end{align*}

Take the square root

\begin{align*} &= \sqrt{36}\\ &= 6 \end{align*}

Video: 223N

Rational exponents and surds

Textbook Exercise 1.3

\(\sqrt{49}\)

\(\sqrt{49} = 7\)

\(\sqrt{36^{-1}}\)

\begin{align*} 36^{-\frac{1}{2}} &= \frac{1}{36^{\frac{1}{2}}} \\ &= \frac{1}{\sqrt{36}} \\ &= \frac{1}{6} \end{align*}

\(\sqrt[3]{6^{-2}}\)

\begin{align*} 6^{-\dfrac{2}{3}} &= \frac{1}{6^{\frac{2}{3}}}\\ &= \frac{1}{\sqrt[3]{6^2}} \\ &= \frac{1}{\sqrt[3]{36}} \end{align*}

\(\sqrt[3]{-\dfrac{64}{27}}\)

\begin{align*} \sqrt[3]{-\dfrac{64}{27}} &= \sqrt[3]{-\frac{4^3}{3^3}} \\ &= \sqrt[3]{ \left( -\frac{4}{3} \right)^3} \\ &= -\frac{4}{3} \end{align*}

\(\sqrt[4]{(16x^4)^3}\)

\begin{align*} \sqrt[4]{(16x^4)^3} &= \left( (16x^4)^3 \right)^{\frac{1}{4}} \\ &= \left( 2^4x^4 \right)^{\frac{3}{4}} \\ &= 2^3x^3 \\ &= 8x^3 \end{align*}

\({s}^{\frac{1}{2}}÷{s}^{\frac{1}{3}}\)

\begin{align*} s^{\frac{1}{2}} \div s^{\frac{1}{3}} &= s^{\frac{1}{2}} \times \frac{1}{s^{\frac{1}{3}}} \\ &= s^{\frac{1}{2} - \frac{1}{3}} \\ &= s^{\frac{3}{6} - \frac{2}{6}} \\ &= s^{\frac{1}{6}} \end{align*}

\({\left(64{m}^{6}\right)}^{\frac{2}{3}}\)

\begin{align*} \left( 64m^6 \right)^{\frac{2}{3}} &= \left( 2^6 \right)^{\frac{2}{3}} \left( m^6 \right)^{\frac{2}{3}} \\ &= \left( 2^4 \right) \left( m^4 \right) \\ &= 16m^4 \end{align*}

\(\dfrac{12m^{ \frac{7}{9}}}{8m^{- \frac{11}{9}}}\)

\begin{align*} \dfrac{12m^{\frac{7}{9}}}{8m^{-\frac{11}{9}}} &= \frac{3}{2} m^{ \frac{7}{9} - \left( - \frac{11}{9} \right)} \\ &= \frac{3}{2} m^{\frac{18}{9}} \\ &= \frac{3}{2}m^{2} \end{align*}

\(\left(5x\right)^0 + 5x^0 - \left(\text{0,25}\right)^{-\text{0,5}} + 8^{\frac{2}{3}}\)

\begin{align*} \left(5x\right)^0 + 5x^0 - \left(\text{0,25}\right)^{-\text{0,5}} + 8^{\frac{2}{3}} &= \left(1 \right) + 5(1)- \left( \frac{1}{4} \right)^{-\frac{1}{2}} + \left(2^3 \right)^{\frac{2}{3}} \\ &= 6 - 4^{\frac{1}{2}} + 4 \\ &= 10 - 2 \\ &= 8 \end{align*}

Use the laws to re-write the following expression as a power of \(x\):

\(x\sqrt{x\sqrt{x\sqrt{x\sqrt{x}}}}\)

\begin{align*} x \sqrt{x \sqrt{x\sqrt{x\sqrt{x}}}} &= x \times x^{\frac{1}{2}} \times x^{\frac{1}{4}} \times x^{\frac{1}{8}} \times x^{\frac{1}{16}} \\ &= x^{\frac{16}{16}} \times x^{\frac{8}{16}} \times x^{\frac{4}{16}} \times x^{\frac{2}{16}}\times x^{\frac{1}{16}} \\ &= x^{\frac{31}{16}} \end{align*}

Simplification of surds (EMBF6)

We have seen in previous examples and exercises that rational exponents are closely related to surds. It is often useful to write a surd in exponential notation as it allows us to use the exponential laws.

The additional laws listed below make simplifying surds easier:

\(\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{ab}\)
\(\sqrt[n]{\dfrac{a}{b}} = \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\)
\(\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}\)
\(\sqrt[n]{a^m} = a^{\frac{m}{n}}\)
\(\left( \sqrt[n]{a} \right)^m = a^{\frac{m}{n}}\)

Worked example 5: Simplifying surds

Show that:

\(\sqrt[n]{a} \times \sqrt[n]{b} = \sqrt[n]{ab}\)
\(\sqrt[n]{\dfrac{a}{b}} = \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\)

\begin{align*} \sqrt[n]{a} \times \sqrt[n]{b} &= a^{\frac{1}{n}} \times b^{\frac{1}{n}} \\ &= (ab)^{\frac{1}{n}} \\ &= \sqrt[n]{ab} \end{align*}
\begin{align*} \sqrt[n]{\frac{a}{b}} &= \left( \frac{a}{b} \right)^{\frac{1}{n}} \\ &= \dfrac{a^{\frac{1}{n}}}{b^{\frac{1}{n}}} \\ &= \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} \end{align*}

Examples:

\(\sqrt{2} \times \sqrt{32} = \sqrt{2 \times 32} = \sqrt{64} = 8\)
\(\dfrac{\sqrt[3]{24}}{\sqrt[3]{3}} = \sqrt[3]{\dfrac{24}{3}} = \sqrt[3]{8} = 2\)
\(\sqrt{\sqrt{81}} = \sqrt[4]{81} = \sqrt[4]{3^4} = 3\)

Like and unlike surds (EMBF7)

Two surds \(\sqrt[m]{a}\) and \(\sqrt[n]{b}\) are like surds if \(m=n\), otherwise they are called unlike surds. For example, \(\sqrt{\frac{1}{3}}\) and \(-\sqrt{61}\) are like surds because \(m = n = 2\). Examples of unlike surds are \(\sqrt[3]{5} \text{ and } \sqrt[5]{7y^3}\) since \(m \ne n\).

Simplest surd form (EMBF8)

We can sometimes simplify surds by writing the radicand as a product of factors that can be further simplified using \(\sqrt[n]{ab} = \sqrt[n]{a} \times \sqrt[n]{b}\).

Video: 2242

Worked example 6: Simplest surd form

Write the following in simplest surd form: \(\sqrt{50}\)

Write the radicand as a product of prime factors

\begin{align*} \sqrt{50} &= \sqrt{5 \times 5 \times 2} \\ &= \sqrt{5^2 \times 2} \end{align*}

Simplify using \(\sqrt[n]{ab} = \sqrt[n]{a} \times \sqrt[n]{b}\)

\begin{align*} &= \sqrt{5^2} \times \sqrt{2} \\ &= 5 \times \sqrt{2} \\ &= 5\sqrt{2} \end{align*}

Sometimes a surd cannot be simplified. For example, \(\sqrt{6}, \sqrt[3]{30} \text{ and } \sqrt[4]{42}\) are already in their simplest form.

Worked example 7: Simplest surd form

Write the following in simplest surd form: \(\sqrt[3]{54}\)

Write the radicand as a product of prime factors

\begin{align*} \sqrt[3]{54} &= \sqrt[3]{3 \times 3 \times 3 \times 2} \\ &= \sqrt[3]{3^3 \times 2} \end{align*}

Simplify using \(\sqrt[n]{ab} = \sqrt[n]{a} \times \sqrt[n]{b}\)

\begin{align*} &= \sqrt[3]{3^3} \times \sqrt[3]{2} \\ &= 3 \times \sqrt[3]{2} \\ &= 3\sqrt[3]{2} \end{align*}

temp text

Worked example 8: Simplest surd form

Simplify: \(\sqrt{\text{147}}+\sqrt{\text{108}}\)

Write the radicands as a product of prime factors

\begin{align*} \sqrt{\text{147}} + \sqrt{\text{108}} &= \sqrt{49 \times 3} + \sqrt{36 \times 3} \\ &= \sqrt{7^2 \times 3} + \sqrt{6^2 \times 3} \end{align*}

Simplify using \(\sqrt[n]{ab} = \sqrt[n]{a} \times \sqrt[n]{b}\)

\begin{align*} &= \left( \sqrt{7^2} \times \sqrt{3} \right) + \left( \sqrt{6^2} \times \sqrt{3} \right)\\ &= \left( 7 \times \sqrt{3} \right) + \left( 6 \times \sqrt{3} \right) \\ &= 7\sqrt{3} + 6\sqrt{3} \end{align*}

Simplify and write the final answer

\[13 \sqrt{3}\]

Worked example 9: Simplest surd form

Simplify: \(\left( \sqrt{20} - \sqrt{5} \right)^2\)

Factorise the radicands were possible

\[\left( \sqrt{20} - \sqrt{5} \right)^2 = \left( \sqrt{4 \times 5} - \sqrt{5} \right)^2\]

Simplify using \(\sqrt[n]{ab} = \sqrt[n]{a} \times \sqrt[n]{b}\)

\begin{align*} &= \left( \sqrt{4} \times \sqrt{5} - \sqrt{5} \right)^2 \\ &= \left( 2 \times \sqrt{5} - \sqrt{5} \right)^2 \\ &= \left( 2\sqrt{5} - \sqrt{5} \right)^2 \end{align*}

Simplify and write the final answer

\begin{align*} &= \left( \sqrt{5} \right)^2 \\ &= 5 \end{align*}

temp text

Worked example 10: Simplest surd form with fractions

Write in simplest surd form: \(\sqrt{75} \times \sqrt[3]{(48)^{-1}}\)

Factorise the radicands were possible

\begin{align*} \sqrt{75} \times \sqrt[3]{(48)^{-1}} &= \sqrt{25 \times 3} \times \sqrt[3]{\frac{1}{48}} \\ &= \sqrt{25 \times 3} \times \frac{1}{\sqrt[3]{8 \times 6}} \end{align*}

Simplify using \(\sqrt[n]{ab} = \sqrt[n]{a} \times \sqrt[n]{b}\)

\begin{align*} &= \sqrt{25} \times \sqrt{3} \times \frac{1}{\sqrt[3]{8} \times \sqrt[3]{6}} \\ &= 5 \times \sqrt{3} \times \frac{1}{2 \times \sqrt[3]{6}} \end{align*}

Simplify and write the final answer

\begin{align*} &= 5\sqrt{3} \times \frac{1}{2\sqrt[3]{6}} \\ &= \frac{5\sqrt{3}}{2\sqrt[3]{6}} \end{align*}

temp text

Simplification of surds

Textbook Exercise 1.4

\(\sqrt[3]{16} \times \sqrt[3]{4}\)

\(\sqrt[3]{16} \times \sqrt[3]{4} = \sqrt[3]{16 \times 4} = \sqrt[3]{64} = 4\)

\(\sqrt{a^2b^3} \times \sqrt{b^5c^4}\)

\(\sqrt{a^2b^3} \times \sqrt{b^5c^4} = \sqrt{a^2b^8c^4} = ab^4c^2\)

\(\dfrac{\sqrt{12}}{\sqrt{3}}\)

\(\dfrac{\sqrt{12}}{\sqrt{3}} = \sqrt{\dfrac{12}{3}} = \sqrt{4} = 2\)

\(\sqrt{x^2y^{13}} \div \sqrt{y^5}\)

\(\sqrt{x^2y^{13}} \div \sqrt{y^5} = \sqrt{\frac{x^2y^{13}}{y^5}} = \sqrt{x^2y^8} = xy^4\)

\(\left( \dfrac{1}{a} - \dfrac{1}{b} \right)^{-1}\)

\begin{align*} \left( \dfrac{1}{a} - \dfrac{1}{b} \right)^{-1} &= \left( \dfrac{b - a}{ab} \right)^{-1} \\ &= \frac{ab}{b - a} \end{align*}

\(\dfrac{b-a}{a^{\frac{1}{2}} - b^{\frac{1}{2}}}\)

\begin{align*} \dfrac{b-a}{a^{\frac{1}{2}} - b^{\frac{1}{2}}} &= - \dfrac{a - b}{a^{\frac{1}{2}} - b^{\frac{1}{2}}} \\ &= - \dfrac{ \left( a^{\frac{1}{2}} \right)^2- \left( b^{\frac{1}{2}} \right)^2}{a^{\frac{1}{2}} - b^{\frac{1}{2}}} \\ &= - \dfrac{ \left( a^{\frac{1}{2}} - b^{\frac{1}{2}} \right)\left( a^{\frac{1}{2}} + b^{\frac{1}{2}} \right) } {a^{\frac{1}{2}} - b^{\frac{1}{2}}} \\ &= - \left( a^{\frac{1}{2}} + b^{\frac{1}{2}} \right) \end{align*}

Rationalising denominators (EMBF9)

It is often easier to work with fractions that have rational denominators instead of surd denominators. By rationalising the denominator, we convert a fraction with a surd in the denominator to a fraction that has a rational denominator.

Worked example 11: Rationalising the denominator

Rationalise the denominator: \[\frac{5x-16}{\sqrt{x}}\]

Multiply the fraction by \(\frac{\sqrt{x}}{\sqrt{x}}\)

Notice that \(\frac{\sqrt{x}}{\sqrt{x}}=1\), so the value of the fraction has not been changed.

\[\frac{5x - 16}{\sqrt{x}} \times \frac{\sqrt{x}}{\sqrt{x}} = \frac{\sqrt{x}(5x - 16)}{\sqrt{x} \times \sqrt{x}}\]

Simplify the denominator

\begin{align*} &= \frac{\sqrt{x}(5x - 16)}{\left( \sqrt{x}\right)^2} \\ &= \frac{\sqrt{x}(5x - 16)}{x} \end{align*}

The term in the denominator has changed from a surd to a rational number. Expressing the surd in the numerator is the preferred way of writing expressions.

Worked example 12: Rationalising the denominator

Write the following with a rational denominator: \[\frac{y-25}{\sqrt{y}+5}\]

Multiply the fraction by \(\frac{\sqrt{y}-5}{\sqrt{y}-5}\)

To eliminate the surd from the denominator, we must multiply the fraction by an expression that will result in a difference of two squares in the denominator.

\[\frac{y-25}{\sqrt{y}+5} \times \frac{\sqrt{y}-5}{\sqrt{y}-5}\]

Simplify the denominator

\begin{align*} &= \frac{(y-25)(\sqrt{y}-5)}{(\sqrt{y}+5)(\sqrt{y}-5)} \\ &= \frac{(y-25)(\sqrt{y}-5)}{(\sqrt{y})^2 -25} \\ &= \frac{(y-25)(\sqrt{y}-5)}{y-25} \\ &= \sqrt{y}-5 \end{align*}

Video: 2249

Rationalising the denominator

Textbook Exercise 1.5

\(\dfrac{10}{\sqrt{5}}\)

\begin{align*} \dfrac{10}{\sqrt{5}} &=\frac{10}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} \\ &=\frac{10\sqrt{5}}{5} \\ &= 2\sqrt{5} \end{align*}

\(\dfrac{3}{\sqrt{6}}\)

\begin{align*} \dfrac{3}{\sqrt{6}} &=\frac{3}{\sqrt{6}} \times \dfrac{\sqrt{6}}{\sqrt{6}} \\ &=\frac{3\sqrt{6}}{6} \\ &=\frac{\sqrt{6}}{2} \end{align*}

\(\dfrac{2}{\sqrt{3}} \div \dfrac{\sqrt{2}}{3}\)

\begin{align*} \dfrac{2}{\sqrt{3}} \div \dfrac{\sqrt{2}}{3} &=\dfrac{2}{\sqrt{3}} \div \dfrac{\sqrt{2}}{3} \\ &=\dfrac{2}{\sqrt{3}} \times \dfrac{3}{\sqrt{2}} \\ &=\dfrac{6}{\sqrt{6}} \times \dfrac{\sqrt{6}}{\sqrt{6}} \\ &=\frac{6\sqrt{6}}{6} \\ &=\sqrt{6} \end{align*}

\(\dfrac{3}{\sqrt{5}-1}\)

\begin{align*} \dfrac{3}{\sqrt{5}-1} &=\dfrac{3}{\sqrt{5}-1} \times \dfrac{\sqrt{5}+1}{\sqrt{5}+1} \\ &=\dfrac{3\sqrt{5}+3}{5-1} \\ &= \dfrac{3\sqrt{5}+3}{4} \end{align*}

\(\dfrac{x}{\sqrt{y}}\)

\begin{align*} \dfrac{x}{\sqrt{y}} &=\dfrac{x}{\sqrt{y}}\times \dfrac{\sqrt{y}}{\sqrt{y}} \\ &=\dfrac{x\sqrt{y}}{y} \end{align*}

\(\dfrac{\sqrt{3} + \sqrt{7}}{\sqrt{2}}\)

\begin{align*} \dfrac{\sqrt{3} + \sqrt{7}}{\sqrt{2}} &=\dfrac{\sqrt{3}+\sqrt{7}}{\sqrt{2}} \times \dfrac{\sqrt{2}}{\sqrt{2}} \\ &=\dfrac{\sqrt{3}\sqrt{2}+\sqrt{7}\sqrt{2}}{2} \\ &=\dfrac{\sqrt{6}+\sqrt{14}}{2} \end{align*}

\(\dfrac{3\sqrt{p} - 4}{\sqrt{p}}\)

\begin{align*} \dfrac{3\sqrt{p} - 4}{\sqrt{p}} &=\dfrac{3\sqrt{p}-4}{\sqrt{p}} \times \dfrac{\sqrt{p}}{\sqrt{p}} \\ &=\dfrac{3\left ( \sqrt{p} \right )^2-4\left ( \sqrt{p} \right )}{p} \\ &=\dfrac{3p-4\sqrt{p}}{p} \end{align*}

\(\dfrac{t-4}{\sqrt{t} + 2}\)

\begin{align*} \dfrac{t-4}{\sqrt{t} + 2} &=\dfrac{t-4}{\sqrt{t}+2} \times \dfrac{\sqrt{t}-2}{\sqrt{t}-2} \\ &=\dfrac{\left ( t-4 \right )\left ( \sqrt{t}-2 \right )}{t-4} \\ &=\sqrt{t}-2 \end{align*}

\(\left( 1 + \sqrt{m} \right)^{-1}\)

\begin{align*} \left( 1 + \sqrt{m} \right)^{-1} &=\frac{1}{1+\sqrt{m}}\times \frac{1-\sqrt{m}}{1-\sqrt{m}} \\ &=\frac{1-\sqrt{m}}{1-m} \end{align*}

\(a \left( \sqrt{a} \div \sqrt{b} \right)^{-1}\)

\begin{align*} a \left( \sqrt{a} \div \sqrt{b} \right)^{-1} &=a\left ( \sqrt{a} \times\frac{1}{\sqrt{b}} \right )^{-1} \\ &=a\left ( \frac{\sqrt{a}}{\sqrt{b}} \right )^{-1} \\ &=a\frac{\sqrt{b}}{\sqrt{a}} \times \frac{\sqrt{a}}{\sqrt{a}} \\ &=\frac{a\sqrt{ab}}{a} \\ &=\sqrt{ab} \end{align*}

1.1 Revision

Table of Contents

1.3 Solving surd equations