\(\sqrt{7}\)
1.1 Revision
|
Next
1.2 Rational exponents and surds
|
Chapter 1: Exponents and surds
1.1 Revision (EMBF2)
The number system (EMBF3)
- Discuss the number system; explain the difference between real and non-real numbers.
- Encourage learners not to use calculators in this chapter.
- Common misconception: \(\pi\) (irrational) ≈ \(\frac{22}{7}\) (rational).
- Explain that the square root of a negative number is non-real.
- Discuss raising a negative number to even and odd powers.
- Explain that surds are a special notation or way of expressing rational exponents.
- Key strategy in manipulation of exponential expressions: express base in terms of its prime factors.
- Emphasize the principle of equivalence and using the additive inverse in the simplification of equations (and not “simply taking term to the other side”).
- Rationalising the denominators is a useful tool for working with special angles in Trigonometry.
- Learners should leave their final answers as mixed fractions.
- Answers should always be written with positive exponents.
The diagram below shows the structure of the number system:
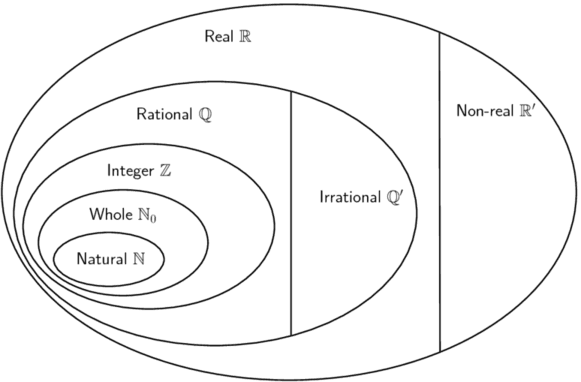
We use the following definitions:
-
\(\mathbb{N}\): natural numbers are \(\{1; \; 2; \; 3; \; \ldots\}\)
-
\(\mathbb{N}_0\): whole numbers are \(\{0; \; 1; \; 2; \; 3; \; \ldots\}\)
-
\(\mathbb{Z}\): integers are \(\{\ldots; \; -3; \; -2; \; -1; \; 0; \; 1; \; 2; \; 3; \; \ldots\}\)
-
\(\mathbb{Q}\): rational numbers are numbers which can be written as \(\frac{a}{b}\) where \(a\) and \(b\) are integers and \(b\ne 0\), or as a terminating or recurring decimal number.
Examples: \(-\frac{7}{2}; \; -\text{2,25}; \; 0; \; \sqrt{9}; \; \text{0,}\dot{8}; \; \frac{23}{1}\)
-
\(\mathbb{Q}'\): irrational numbers are numbers that cannot be written as a fraction with the numerator and denominator as integers. Irrational numbers also include decimal numbers that neither terminate nor recur.
Examples: \(\sqrt{3}; \; \sqrt[5]{2}; \; \pi; \; \frac{1 + \sqrt{5}}{2}; \; \text{1,27548}\ldots\)
-
\(\mathbb{R}\): real numbers include all rational and irrational numbers.
-
\(\mathbb{R}'\): non-real numbers or imaginary numbers are numbers that are not real.
Examples: \(\sqrt{-25}; \; \sqrt[4]{-1}; \; -\sqrt{-\frac{1}{16}}\)
The number system
Use the list of words below to describe each of the following numbers (in some cases multiple words will be applicable):
- Natural (\(\mathbb{N}\))
- Whole (\(\mathbb{N}_0\))
- Integer (\(\mathbb{Z}\))
- Rational (\(\mathbb{Q}\))
- Irrational (\(\mathbb{Q}'\))
- Real (\(\mathbb{R}\))
- Non-real (\(\mathbb{R}'\))
\(\text{0,01}\)
\(16\frac{2}{5}\)
\(\sqrt{6\frac{1}{4}}\)
\(\text{0}\)
\(2\pi\)
\(-\text{5,3}\dot{8}\)
\(\frac{1-\sqrt{2}}{2}\)
\(-\sqrt{-3}\)
\((\pi)^2\)
\(-\frac{9}{11}\)
\(\sqrt[3]{-8}\)
\(\frac{22}{7}\)
\(\text{2,45897}\ldots\)
\(\text{0,}\overline{65}\)
\(\sqrt[5]{-32}\)
Laws of exponents (EMBF4)
We use exponential notation to show that a number or variable is multiplied by itself a certain number of times. The exponent, also called the index or power, indicates the number of times the multiplication is repeated.
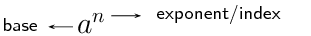
Examples:
- \(2 \times 2 \times 2 \times 2 = 2^4\)
- \(\text{0,71} \times \text{0,71} \times \text{0,71} = (\text{0,71})^3\)
- \((\text{501})^2 = \text{501} \times \text{501}\)
- \(k^6 = k \times k \times k \times k \times k \times k\)
For \(x^2\), we say \(x\) is squared and for \(y^3\), we say that \(y\) is cubed. In the last example we have \(k^6\); we say that \(k\) is raised to the sixth power.
We also have the following definitions for exponents. It is important to remember that we always write the final answer with a positive exponent.
-
\({a}^{0}=1\) (\(a \ne 0\) because \(0^0\) is undefined)
-
\({a}^{-n}=\frac{1}{{a}^{n}}\) (\(a \ne 0\) because \(\frac{1}{0}\) is undefined)
Examples:
- \(5^{-2} = \dfrac{1}{5^2} = \dfrac{1}{25}\)
- \((-36)^0 x = (1)x = x\)
- \(\dfrac{7p^{-1}}{q^{3}t^{-2}} = \dfrac{7t^2}{pq^3}\)
We use the following laws for working with exponents:
- \({a}^{m} \times {a}^{n}={a}^{m+n}\)
- \(\frac{{a}^{m}}{{a}^{n}}={a}^{m-n}\)
- \({\left(ab\right)}^{n}={a}^{n}{b}^{n}\)
- \({\left(\frac{a}{b}\right)}^{n}=\frac{{a}^{n}}{{b}^{n}}\)
- \({\left({a}^{m}\right)}^{n}={a}^{mn}\)
Worked example 1: Laws of exponents
Simplify the following:
- \(5(m^{2t})^p \times 2(m^{3p})^t\)
- \(\dfrac{8k^3x^2}{(xk)^2}\)
- \(\dfrac{2^2 \times 3 \times 7^4}{(7 \times 2)^4}\)
- \(3(3^b)^a\)
- \(5(m^{2t})^p \times 2(m^{3p})^t = 10m^{2pt + 3pt} = 10m^{5pt}\)
- \(\dfrac{8k^3x^2}{(xk)^2} = \dfrac{8k^3x^2}{x^2k^2} = 8k^{(3-2)}x^{(2-2)} = 8k^1x^0 = 8k\)
- \(\dfrac{2^2 \times 3 \times 7^4}{(7 \times 2)^4} = \dfrac{2^2 \times 3 \times 7^4}{7^4 \times 2^4} = 2^{(2-4)} \times 3 \times 7^{(4-4)} = 2^{-2} \times 3 = \frac{3}{4}\)
- \(3(3^b)^a = 3 \times 3^{ab} = 3^{ab + 1}\)
Worked example 2: Laws of exponents
Simplify:\(\dfrac{3^m - 3^{m+1}}{4 \times 3^m - 3^m}\)
Simplify to a form that can be factorised
\[\dfrac{3^m - 3^{m+1}}{4 \times 3^m - 3^m} = \dfrac{3^m - (3^{m} \times 3)}{4 \times 3^m - 3^m}\]Take out a common factor
\[\begin{align*} &= \dfrac{3^m(1 - 3)}{3^m(4 - 1)} \end{align*}\]Cancel the common factor and simplify
\[\begin{align*} &= \frac{1 - 3}{4 - 1} \\ &= - \frac{2}{3} \end{align*}\]Laws of exponents
Simplify the following:
\(4 \times 4^{2a} \times 4^2 \times 4^a\)
\(\dfrac{3^2}{2^{-3}}\)
\((3p^5)^2\)
\(\dfrac{k^2k^{3x-4}}{k^x}\)
\((5^{z-1})^2+5^z\)
\((\frac{1}{4})^0\)
\((x^2)^5\)
\(\left( \frac{a}{b} \right)^{-2}\)
\((m+n)^{-1}\)
\(2(p^t)^s\)
\(\dfrac{1}{\left(\frac{1}{a}\right)^{-1}}\)
\(\frac{k^{0}}{k^{-1}}\)
\(\dfrac{-2}{-2^{-a}}\)
\(\dfrac{-h}{(-h)^{-3}}\)
\(\left( \dfrac{a^2b^3}{c^3d} \right)^2\)
\(10^{7}(7^{0}) \times 10^{-6}(-6)^{0}-6\)
\(m^3n^2 \div nm^2 \times \frac{mn}{2}\)
\((2^{-2}-5^{-1})^{-2}\)
\((y^2)^{-3} \div \left( \frac{x^2}{y^3} \right)^{-1}\)
\(\dfrac{2^{c-5}}{2^{c-8}}\)
\(\dfrac{2^{9a} \times 4^{6a} \times 2^2}{8^{5a}}\)
\(\dfrac{20t^5p^{10}}{10t^4p^9}\)
\(\left( \dfrac{9q^{-2s}}{q^{-3s}y^{-4a-1}} \right)^2\)
| Table of Contents |
Next
1.2 Rational exponents and surds
|
