\(y - 1 = 4x\) and \(4y + x + 2 = 0\)
\(\therefore\)Perpendicular lines.
|
Previous
4.4 Parallel lines
|
Next
4.6 Summary
|
Deriving the formula: \(m_1 \times m_2 = -1\)
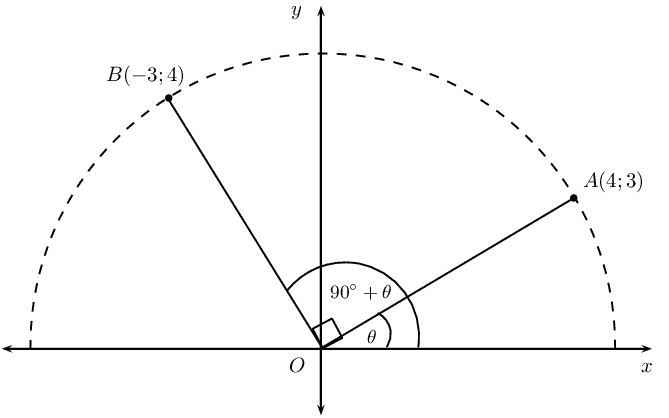
Consider the point \(A(4;3)\) on the Cartesian plane with an angle of inclination \(A\hat{O}X = \theta\). Rotate through an angle of \(\text{90}\text{°}\) and place point \(B\) at \((-3;4)\) so that we have the angle of inclination \(B\hat{O}X = \text{90}\text{°}+ \theta\).
We determine the gradient of \(OA\): \begin{align*} m_{OA} &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{3 - 0}{4 - 0} \\ &= \frac{3}{4} \end{align*}
And determine the gradient of \(OB\): \begin{align*} m_{OB} &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{4 - 0}{-3 - 0} \\ &= \frac{4}{-3} \end{align*}
By rotating through an angle of \(\text{90}\text{°}\) we know that \(OB \perp OA\): \begin{align*} m_{OA} \times m_{OB} &= \frac{3}{4} \times \frac{4}{-3} \\ &= -1 \end{align*}
We can also write that
\[m_{OA} = -\frac{1}{m_{OB}}\]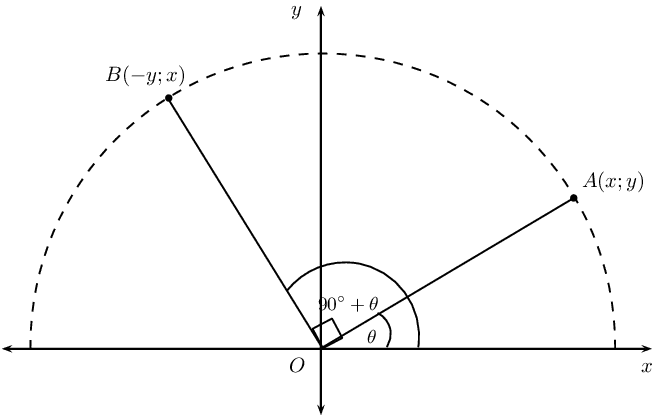
If we have the general point \(A(x;y)\) with an angle of inclination \(A\hat{O}X = \theta\) and point \(B(-y;x)\) such that \(B\hat{O}X = \text{90}\text{°}+ \theta\), then we know that
\begin{align*} m_{OA} &= \frac{y}{x} \\ m_{OB} &= -\frac{x}{y} \\ \therefore m_{OA} \times m_{OB}&= \frac{y}{x} \times -\frac{x}{y} \\ &= -1 \end{align*}Another method of determining the equation of a straight line is to be given a point on the line, \(\left({x}_{1};{y}_{1}\right)\), and the equation of a line which is perpendicular to the unknown line. Let the equation of the unknown line be \(y = m_1x + c_1\) and the equation of the given line be \(y = m_2x + c_2\).
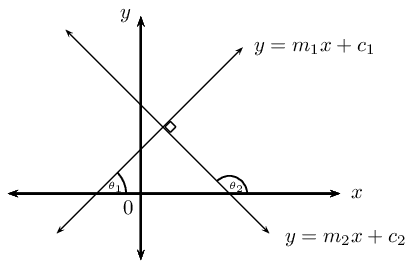
If the two lines are perpendicular then
\[m_1 \times m_2 = -1\]
Note: this rule does not apply to vertical or horizontal lines.
When determining the gradient of a line using the coefficient of \(x\), make sure the given equation is written in the gradient–intercept (standard) form \(y = mx + c\). Then we know that \[m_1 = -\frac{1}{m_2}\]
Substitute the value of \(m_1\) and the given point \(\left({x}_{1};{y}_{1}\right)\), into the gradient–intercept form of the straight line equation \(y-y_1 = m(x-x_1)\) and determine the equation of the unknown line.
Determine the equation of the straight line passing through the point \(T(2;2)\) and perpendicular to the line \(3y + 2x - 6 = 0\).
Let the gradient of the unknown line be \(m_1\) and the given gradient be \(m_2\). We write the given equation in gradient–intercept form and determine the value of \(m_2\).
\begin{align*} 3y + 2x - 6 &= 0 \\ 3y & = -2x + 6 \\ y & = -\frac{2}{3}x + 2\\ \therefore m_2 & = -\frac{2}{3} \end{align*}We know that the two lines are perpendicular, therefore \(m_1 \times m_2 = -1\). Therefore \(m_1 = \frac{3}{2}\).
Substitute \(m_1 = \frac{3}{2}\).
\[y - y_1 = \frac{3}{2}(x - x_1)\]Substitute the given point \(T(2;2)\).
\begin{align*} y - 2 & = \frac{3}{2}(x - 2) \\ y - 2& = \frac{3}{2}x - 3\\ y & = \frac{3}{2}x - 1 \end{align*}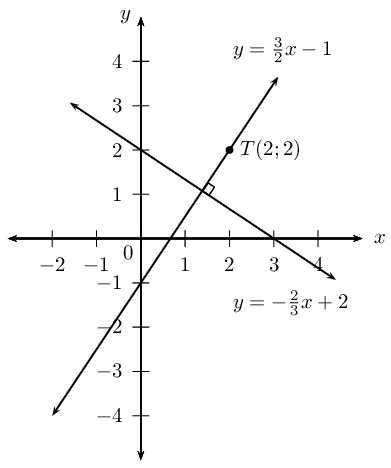
A sketch was not required, but it is useful for checking the answer.
The equation of the straight line is \(y = \frac{3}{2}x - 1\).
Determine the equation of the straight line passing through the point \((2;\frac{1}{3})\) and perpendicular to the line with an angle of inclination of \(\text{71,57}\)\(\text{°}\).
Let the gradient of the unknown line be \(m_1\) and let the given gradient be \(m_2\).
\begin{align*} m_{2} & = \tan \theta \\ & = \tan \text{71,57}\text{°} \\ & = \text{3,0} \end{align*}Since we are given that the two lines are perpendicular,
\begin{align*} m_{1} \times m_{2} &= -1 \\ \therefore m_{1} &= - \frac{1}{3} \end{align*}\[y - y_1 = m(x - x_1)\]
Substitute the gradient \(m_{1} = -\frac{1}{3}\).
\[y - y_1 = -\frac{1}{3}(x - x_1)\]
Substitute the given point \((2;\frac{1}{3})\).
\begin{align*} y - \left(\frac{1}{3}\right) & = -\frac{1}{3}(x - 2) \\ y -\frac{1}{3} & = -\frac{1}{3}x + \frac{2}{3}\\ y & = -\frac{1}{3}x + 1 \end{align*}The equation of the straight line is \(y = -\frac{1}{3}x + 1\).
Calculate whether or not the following two lines are perpendicular:
\(y - 1 = 4x\) and \(4y + x + 2 = 0\)
\(\therefore\)Perpendicular lines.
\(10x = 5y - 1\) and \(5y - x - 10 = 0\)
\(\therefore\)Not perpendicular lines.
\(x = y - 5\) and the line passing through \((-1;\frac{5}{4})\) and \((3;-\frac{11}{4})\)
\(\therefore\)Perpendicular lines.
\(y = 2\) and \(x = 1\)
\(\frac{y}{3} = x\) and \(3y + x = 9\)
\(\therefore\)Perpendicular lines.
\(1 - 2x = y\) and the line passing through \((2;-1)\) and \((-1;5)\)
\(\therefore\)Not perpendicular lines.
\(y = x + 2\) and \(2y + 1 = 2x\)
\(\therefore\)Not perpendicular lines.
Determine the equation of the straight line that passes through the point \((-2;-4)\) and is perpendicular to the line \(y + 2x = 1\).
Determine the equation of the straight line that passes through the point \((2;-7)\) and is perpendicular to the line \(5y - x = 0\).
Determine the equation of the straight line that passes through the point \((3;-1)\) and is perpendicular to the line with angle of inclination \(\theta = \text{135}\text{°}\).
Determine the equation of the straight line that passes through the point \((-2;\frac{2}{5})\) and is perpendicular to the line \(y = \frac{4}{3}\).
|
Previous
4.4 Parallel lines
|
Table of Contents |
Next
4.6 Summary
|