What is the NPK ratio of a starter fertiliser?
\(\text{18}\):\(\text{24}\):\(\text{6}\)
|
Previous
14.2 Nutrients
|
Next
14.4 The fertiliser industry
|
The importance of fertilisers is discussed and how to use NPK ratios in calculations.
Refer to the Chemical Industries Resource Pack for more information.
Plants are only able to absorb nutrients from the soil when they are dissolved in water so that their root systems can absorb the nutrients. Nitrogen gas (\(\text{N}_{2}\)) for example, cannot be absorbed in the gas form, and needs to be changed into an ion that is soluble in water, for example the nitrate ion (\(\text{NO}_{3}^{-}\)). In the same way phosphorus is absorbed as phosphate ions (\(\text{PO}_{4}^{3-}\)).
Plants will grow best in soil that is able to provide sufficient nutrients to them. Natural processes, like the nitrogen cycle, replace nutrients in the soil. However, these natural processes of maintaining soil nutrients take a long time. As populations grow and the demand for food increases, the soil has to supply nutrients faster than the natural processes can sustain. This places more and more strain on the soil to be able to produce a crop.
Often, cultivation practices don’t give the soil enough time to recover and to replace the nutrients that have been lost. Today, fertilisers play a very important role in restoring soil nutrients so that crop yields can stay high. Some of these fertilisers are organic (e.g. compost, manure and fishmeal), which means that they started off as part of something living. Industrial (commercial) fertilisers are inorganic (for example ammonium nitrate (\(\text{NH}_{4}\text{NO}_{3}\)) or super phosphates (\(\text{Ca}(\text{H}_{2}\text{PO}_{4})_{2}\)) and have the advantage of being in a soluble form that can be absorbed by a plant immediately.
Fertilisers usually provide the three major plant nutrients (nitrogen, phosphorus and potassium). Fertilisers are in general applied to the soil so that the nutrients are absorbed by plants through their roots.

Figure 14.2: Examples of (a) organic (compost) and (b) inorganic (industrially made) fertilisers indicating the NPK ratio that will be discussed later.
Photos by Kessner Photography on wikipedia and Elvera Viljoen in the UCT Chemical Engineering Chemical Industries Resource pack.
Fertiliser packaging contains a set of numbers, for example \(\text{6}\):\(\text{1}\):\(\text{5}\) (see Figure 14.2). These numbers are called the NPK ratio, and they give the mass ratio of nitrogen, phosphorus and potassium in the fertiliser.
The NPK ratio expresses the content of each nutrient as a percentage of N, P and K in this order. A number in brackets after this ratio indicates the percentage by mass of N, P and K that is present in the fertiliser (what percentage of the total fertiliser is N, P and K). For example:
38% of the total fertiliser is nitrogen, phosphorus or potassium.
\(\%\) N: \(\text{3}\) in every \(\text{9}\) parts of the 38% contains nitrogen (N)
\(\%\) P: \(\text{1}\) in every \(\text{9}\) parts of the 38% contains phosphorus (P)
\(\%\) K: \(\text{5}\) in every \(\text{9}\) parts of the 38% contains potassium (K)
Table 14.3 below gives an idea of the amounts of nitrogen, phosphorus and potassium there are in different types of fertilisers.
A starter fertiliser is usually used when seeds or young plants are planted. It has high concentrations of nitrogen, to boost plant growth, and phosphorus to boost root growth.

|
Description |
Grade (NPK ratio) |
|
Ammonium nitrate |
\(\text{34}\):\(\text{0}\):\(\text{0}\) |
|
Urea |
\(\text{46}\):\(\text{0}\):\(\text{0}\) |
|
Bone meal |
\(\text{4}\):\(\text{21}\):\(\text{1}\) |
|
Seaweed |
\(\text{1}\):\(\text{1}\):\(\text{5}\) |
|
Starter fertilisers |
\(\text{18}\):\(\text{24}\):\(\text{6}\) |
|
Equal NPK fertilisers |
\(\text{12}\):\(\text{12}\):\(\text{12}\) |
|
High N, low P and medium K fertilisers |
\(\text{25}\):\(\text{5}\):\(\text{15}\) |
Table 14.3: Common grades of some fertiliser materials.
Depending on the types of plants you are growing, and the growth stage they are in, you may need to use a fertiliser with a slightly different ratio. For example, if you want to encourage root growth in your plant you might choose a fertiliser with a greater ratio of phosphorus in it. The main functions of each nutrient (N, P, K) are given in Table 14.4. Remember to refer to Table 14.1 and Table 14.2 as well.
|
Nutrient |
Promotes |
When to use |
|
Nitrogen (N) |
leafy plant growth, faster plant growth |
on lawns and other plants with lots of green leaves |
|
Phosphorus (P) |
strong roots, healthy fruit, blooming |
on flowers and flower beds |
|
Potassium (K) |
disease resistance, growth of fruit |
on fruit bearing plants |
Table 14.4: The types of plant growth different nutrients promote.
Some countries express the phosphorus content as \(\text{P}_{2}\text{O}_{5}\) and potassium content as \(\text{K}_{2}\text{O}\). South Africa expresses the NPK ratio in terms of the elements present as explained above. The rest of the fertiliser (62%) is made up of fillers, such as gypsum, lime and sand. Other micronutrients, such as calcium (\(\text{Ca}\)), sulfur (\(\text{S}\)) and magnesium (\(\text{Mg}\)), are often added to the mixture.
Calculate the mass of nitrogen (N), phosphorus (P) and potassium (K) that is present in \(\text{500}\) \(\text{g}\) of industrial fertiliser with a NPK ratio of \(\text{5}\):\(\text{2}\):\(\text{3}\) (\(\text{40}\)).
40% of the sample contains nutrients, therefore:
40% of \(\text{500}\) \(\text{g}\) = \(\text{0,4}\) x \(\text{500}\) \(\text{g}\) = \(\text{200}\) \(\text{g}\) which contains nutrients.
For every \(\text{5}\) units of nitrogen there are \(\text{2}\) units of phosphorus and \(\text{3}\) units of potassium so the total number of units is \(\text{10}\).
\(\text{5}\) of the \(\text{10}\) units are nitrogen, therefore:
\(\dfrac{5}{10}\times\) \(\text{200}\) \(\text{g}\) = \(\text{100}\) \(\text{g}\) will be nitrogen (N).
\(\text{2}\) of the \(\text{10}\) units are phosphorus, therefore:
\(\dfrac{2}{10}\times\) \(\text{200}\) \(\text{g}\) = \(\text{40}\) \(\text{g}\) will be phosphorus (P).
\(\text{3}\) of the \(\text{10}\) units are potassium, therefore:
\(\dfrac{3}{10}\times\) \(\text{200}\) \(\text{g}\) = \(\text{60}\) \(\text{g}\) will be potassium (K).
Calculate the mole ratio of an industrial fertiliser with the NPK ratio of \(\text{5}\):\(\text{2}\):\(\text{3}\) (\(\text{40}\)).
As we are calculating the mole ratio, any amount of fertiliser can be assumed.
As in the previous worked example the ratio is \(\text{5}\):\(\text{2}\):\(\text{3}\) (\(\text{40}\)), so the mass of nutrients will be \(\text{200}\) \(\text{g}\). Therefore:
The mass of N = \(\dfrac{5}{10}\times\) \(\text{200}\) \(\text{g}\) = \(\text{100}\) \(\text{g}\).
The mass of P = \(\dfrac{2}{10}\times\) \(\text{200}\) \(\text{g}\) = \(\text{40}\) \(\text{g}\).
The mass of K = \(\dfrac{3}{10}\times\) \(\text{200}\) \(\text{g}\) = \(\text{60}\) \(\text{g}\).
\(\text{n} = \dfrac{\text{m}}{\text{M}}\)
The molar mass (M) for N = \(\text{14,0}\) \(\text{g·mol$^{-1}$}\)
Therefore n for nitrogen = \(\dfrac{\text{100}{\text{ g}}}{\text{14,0}{\text{ g·mol}}^{-1}}\) = \(\text{7,14}\) \(\text{mol}\)
M for P = \(\text{31,0}\) \(\text{g·mol$^{-1}$}\)
Therefore n for phosphorus = \(\dfrac{\text{40}{\text{ g}}}{\text{31,0}{\text{ g·mol}}^{-1}}\) = \(\text{1,29}\) \(\text{mol}\)
M for K = \(\text{39,1}\) \(\text{g·mol$^{-1}$}\)
Therefore n for potassium = \(\dfrac{\text{60}{\text{ g}}}{\text{39,1}{\text{ g·mol}}^{-1}}\) = \(\text{1,53}\) \(\text{mol}\)
N:P:K mole ratio = \(\text{7,14}\) : \(\text{1,29}\) : \(\text{1,53}\)
To get the mole ratio divide all the numbers by the smallest number (\(\text{1,29}\)):
\(\text{5,5}\) : \(\text{1}\) : \(\text{1,2}\)
The ratio should be expressed as whole numbers:
\(\text{55}\) : \(\text{10}\) : \(\text{12}\)
Note: If the percentage purity is not given (the number in brackets – e.g. 40 in the worked example above), then you can assume that it is a 100% pure fertiliser and no fillers were added.
As mentioned previously, in South Africa the NPK ratio is expressed in elemental form, for example the P in the ratio refers to the mass of the element phosphorus (P). However, in some countries the ratios are expressed in compound form: \(\text{N}\):\(\text{P}_{2}\text{O}_{5}\):\(\text{K}_{2}\text{O}\). Nitrogen still refers to the element nitrogen, but phosphorus and potassium refer to the compounds phosphorus pentoxide (\(\text{P}_{2}\text{O}_{5}\)) and potassium oxide (\(\text{K}_{2}\text{O}\)). This example will show you how to calculate the mass or moles when a compound ratio is given.
Calculate the moles of phosphorus (P) in \(\text{120}\) \(\text{g}\) of a fertiliser with the \(\text{N}\):\(\text{P}_{2}\text{O}_{5}\):\(\text{K}_{2}\text{O}\) mass ratio of \(\text{4}\):\(\text{3}\):\(\text{8}\) (\(\text{50}\)).
50% of the sample contains nutrients.
50% of \(\text{120}\) \(\text{g}\) = \(\text{0,5}\) x \(\text{120}\) \(\text{g}\) = \(\text{60}\) \(\text{g}\) which contains nutrients.
The \(\text{N}\):\(\text{P}_{2}\text{O}_{5}\):\(\text{K}_{2}\text{O}\) ratio is \(\text{4}\) : \(\text{3}\) : \(\text{8}\). \(\text{4}\) + \(\text{3}\) + \(\text{8}\) = \(\text{15}\). Therefore:
\(\text{3}\) of the \(\text{15}\) units are \(\text{P}_{2}\text{O}_{5}\).
The mass of \(\text{P}_{2}\text{O}_{5}\) = \(\dfrac{3}{15} \times\) \(\text{60}\) \(\text{g}\) = \(\text{12}\) \(\text{g}\).
\(\text{n} = \dfrac{\text{m}}{\text{M}}\)
M(\(\text{P}_{2}\text{O}_{5}\)) = \(\text{2}\) x \(\text{31,0}\) \(\text{g·mol$^{-1}$}\) + \(\text{5}\) x \(\text{16,0}\) \(\text{g·mol$^{-1}$}\) = \(\text{142,0}\) \(\text{g·mol$^{-1}$}\)
Therefore n(\(\text{P}_{2}\text{O}_{5}\)) = \(\dfrac{\text{12}{\text{ g}}}{\text{142,0}{\text{ g·mol}}^{-1}}\) = \(\text{0,0845}\) \(\text{mol}\)
For every \(\text{1}\) mole of \(\text{P}_{2}\text{O}_{5}\) there are \(\text{2}\) moles of \(\text{P}\) atoms.
Therefore, n(\(\text{P}\)) = \(\text{2}\) x \(\text{0,0845}\) \(\text{mol}\) = \(\text{0,17}\) \(\text{mol}\)
For this activity leaners should work on their own.
Solutions:
The NPK ratio for bone meal is \(\text{4}\) : \(\text{21}\) : \(\text{1}\). \(\text{4}\) + \(\text{21}\) + \(\text{1}\) = \(\text{26}\).
\(\text{21}\) of the \(\text{26}\) units are \(\text{P}\).
Assume a 100% purity of the bone meal, so the entire \(\text{250}\) \(\text{g}\) is nutrients.
m(\(\text{P}\)) = \(\dfrac{21}{26} \times\) \(\text{250}\) \(\text{g}\) = \(\text{201,92}\) \(\text{g}\)
Assume a 100% purity of the ammonium nitrate, so the entire \(\text{200}\) \(\text{g}\) is \(\text{NH}_{4}\text{NO}_{3}\).
The NPK ratio for ammonium nitrate is \(\text{34}\) : \(\text{0}\) : \(\text{0}\). Therefore there is no phosphorus or potassium in the fertiliser.
m(\(\text{NH}_{4}\text{NO}_{3}\)) = \(\text{200}\) \(\text{g}\)
M(\(\text{NH}_{4}\text{NO}_{3}\)) = (\(\text{2}\) x \(\text{14,0}\) + \(\text{4}\) x \(\text{1,01}\) + \(\text{3}\) x \(\text{16,0}\)) \(\text{g·mol$^{-1}$}\) = \(\text{80,04}\) \(\text{g·mol$^{-1}$}\)
n(\(\text{NH}_{4}\text{NO}_{3}\)) = \(\dfrac{\text{m (g)}}{\text{M (g·mol}^{-1}{\text{)}}} = \dfrac{\text{200} {\text{ g}}}{\text{80,04} {\text{ g·mol}}^{-1}}\) = \(\text{2,5}\) \(\text{mol}\)
For every \(\text{1}\) mole of \(\text{NH}_{4}\text{NO}_{3}\) there are \(\text{2}\) moles of \(\text{N}\).
n(\(\text{N}\)) = \(\text{2}\) x \(\text{2,5}\) \(\text{mol}\) = \(\text{5}\) \(\text{mol}\)
The NPK ratio for seaweed is \(\text{1}\) : \(\text{1}\) : \(\text{5}\). \(\text{1}\) + \(\text{1}\) + \(\text{5}\) = \(\text{7}\).
\(\text{5}\) of the \(\text{7}\) units are postassium (\(\text{K}\)).
Assume a 100% purity of the seaweed, so the entire \(\text{100}\) \(\text{g}\) is nutrients.
m(\(\text{K}\)) = \(\dfrac{5}{7} \times\) \(\text{100}\) \(\text{g}\) = \(\text{71,4}\) \(\text{g}\)
40% of the sample is nutrients. The mass of nutrients in the sample is: \(\text{0,4}\) x \(\text{100}\) \(\text{g}\) = \(\text{40}\) \(\text{g}\)
The \(\text{N}:\text{P}_{2}\text{O}_{5}\text{K}_{2}\text{O}\) ratio is \(\text{5}\) : \(\text{1}\) : \(\text{2}\). \(\text{5}\) + \(\text{1}\) + \(\text{2}\) = \(\text{8}\).
\(\text{2}\) of the \(\text{8}\) units are \(\text{K}_{2}\text{O}\).
m(\(\text{K}_{2}\text{O}\)) = \(\dfrac{2}{8} \times\) \(\text{40}\) \(\text{g}\) = \(\text{10}\) \(\text{g}\)
M(\(\text{K}_{2}\text{O}\)) = (\(\text{2}\) x \(\text{39,1}\) + \(\text{16,0}\)) \(\text{g·mol$^{-1}$}\) = \(\text{94,2}\) \(\text{g·mol$^{-1}$}\)
n(\(\text{K}_{2}\text{O}\)) = \(\dfrac{\text{10} {\text{ g}}}{\text{94,2} {\text{ g·mol}}^{-1}}\)= \(\text{0,106}\) \(\text{mol}\)
For every \(\text{1}\) mole of \(\text{K}_{2}\text{O}\) there are \(\text{2}\) moles of \(\text{K}\).
n(\(\text{K}\)) = \(\text{2}\) x \(\text{0,106}\) \(\text{mol}\) = \(\text{0,21}\) \(\text{mol}\)
Use Table 14.3, if needed, to answer the following questions:
Calculate the mass of phosphorus that is present in \(\text{250}\) \(\text{g}\) of bone meal.
Calculate the moles of nitrogen that are present in \(\text{200}\) \(\text{g}\) of ammonium nitrate (\(\text{NH}_{4}\text{NO}_{3}\)).
Calculate the mass of potassium that is present in \(\text{100}\) \(\text{g}\) of seaweed.
Calculate the number of moles of potassium in \(\text{100}\) \(\text{g}\) of a commercial fertiliser with the \(\text{N}\):\(\text{P}_{2}\text{O}_{5}\):\(\text{K}_{2}\text{O}\) mass ratio of \(\text{5}\):\(\text{1}\):\(\text{2}\) (\(\text{40}\)).
A starter fertiliser is usually used when seeds or young plants are planted.
Use Table 14.3 to answer the following questions.
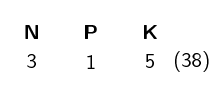
What is the NPK ratio of a starter fertiliser?
\(\text{18}\):\(\text{24}\):\(\text{6}\)
Which nutrient is present in the lowest concentration?
potassium (\(\text{K}\))
Do you think an equal NPK fertiliser will be a good starter fertiliser for new plants? Explain your answer using information from Tables Table 14.1 - Table 14.4.
No. New plants need nitrogen (to boost plant growth) and phosphorus (for root growth). An equal NPK fertiliser has equal amounts of N, P and K and therefore would not promote new plant growth as much. An actual starter fertiliser contains much higher amounts of nitrogen and phosphorus (\(\text{18}\):\(\text{24}\):\(\text{6}\)).
Do you think bone meal is a good fertiliser to use for flowering plants? Explain your answer using Tables Table 14.1 - Table 14.4.
Yes. The NPK ratio of bone meal is \(\text{4}\) : \(\text{21}\) : \(\text{1}\). Bone meal has a high phosphorus (P) content (\(\text{21}\) of \(\text{26}\) units are P). Phosphorus is good for flowering plants so a high phosphorus content would make bone meal a good fertiliser to use.
Determine the mass of each of the nutrient components in a \(\text{600}\) \(\text{g}\) bag of the fertiliser shown in Figure 14.2 (it is produced in South Africa).
The NPK mass ratio is \(\text{6}\) : \(\text{1}\) : \(\text{5}\) (\(\text{22}\)). \(\text{6}\) + \(\text{1}\) + \(\text{5}\) = \(\text{12}\).
Determine the mass of the total nutrients in the fertiliser sample:
22% of the sample contains nutrients, therefore:
The mass of nutrients in the sample = \(\text{0,22}\) x \(\text{600}\) \(\text{g}\) = \(\text{132}\) \(\text{g}\)
\(\text{6}\) of the \(\text{12}\) units are nitrogen, therefore:
m(\(\text{N}\)) = \(\dfrac{6}{12}\times\) \(\text{132}\) \(\text{g}\) = \(\text{66}\) \(\text{g}\)
\(\text{1}\) of the \(\text{12}\) units is phosphorus, therefore:
m(\(\text{P}\)) = \(\dfrac{1}{12}\times\) \(\text{132}\) \(\text{g}\) = \(\text{11}\) \(\text{g}\)
\(\text{5}\) of the \(\text{12}\) units are potassium, therefore:
m(\(\text{K}\)) = \(\dfrac{5}{12}\times\) \(\text{132}\) \(\text{g}\) = \(\text{55}\) \(\text{g}\)
You have determined that your vegetable garden will need \(\text{12}\) \(\text{g}\) of nitrogen. The fertiliser you have has \(\text{4}\):\(\text{2}\):\(\text{3}\) (\(\text{40}\)) written on the packet. How many grams of fertiliser will you need for your garden?
The NPK mass ratio is \(\text{4}\) : \(\text{2}\) : \(\text{3}\) (\(\text{40}\)). \(\text{4}\) + \(\text{2}\) + \(\text{3}\) = \(\text{9}\).
\(\text{4}\) of the \(\text{9}\) units are nitrogen and \(\text{12}\) \(\text{g}\) of nitrogen is needed, therefore:
\(\dfrac{4}{9}\times\) total mass of nutrients required = \(\text{12}\) \(\text{g}\).
Total mass of nutrients required = \(\text{12}\) \(\text{g}\) \(\times \dfrac{9}{4}\) = \(\text{27}\) \(\text{g}\)
40% of the sample contains nutrients, therefore:
40% of fertiliser required = \(\text{27}\) \(\text{g}\)
Total fertiliser required = \(\dfrac{\text{27}{\text{ g}}}{\text{0,40}}\)= \(\text{67,5}\) \(\text{g}\).
How many moles of potassium is present in \(\text{150}\) \(\text{g}\) of commercial fertiliser with the \(\text{N}\):\(\text{P}_{2}\text{O}_{5}\):\(\text{K}_{2}\text{O}\) mass ratio of \(\text{1}\):\(\text{2}\):\(\text{5}\).
The \(\text{N}\):\(\text{P}_{2}\text{O}_{5}\):\(\text{K}_{2}\text{O}\) ratio is \(\text{1}\) : \(\text{2}\) : \(\text{5}\). \(\text{1}\) + \(\text{2}\) + \(\text{5}\) = \(\text{8}\).
No percentage purity is given, therefore assume 100% purty. So the entire \(\text{15}\) \(\text{g}\) is nutrients.
\(\text{5}\) units of the \(\text{8}\) units are \(\text{K}_{2}\text{O}\)
M(\(\text{K}_{2}\text{O}\)) = (\(\text{2}\) x \(\text{39,1}\) + \(\text{16,0}\)) \(\text{g·mol$^{-1}$}\) = \(\text{94,2}\) \(\text{g·mol$^{-1}$}\)
m(\(\text{K}_{2}\text{O}\)) = \(\dfrac{5}{8}\times\) \(\text{150}\) \(\text{g}\) = \(\text{93,75}\) \(\text{g}\).
n(\(\text{K}_{2}\text{O}\)) = \(\dfrac{\text{m (g)}} {\text{M(g·mol}^{-1}{\text{)}}} = \dfrac{\text{93,75} {\text{g}}}{\text{94,2}{\text{ g·mol}}^{-1}}\) = \(\text{0,995}\) \(\text{mol}\)
For every \(\text{1}\) mole of \(\text{K}_{2}\text{O}\) there are \(\text{2}\) moles of \(\text{K}\) atoms.
Therefore, n(\(\text{K}\)) = \(\text{2}\) x \(\text{0,995}\) \(\text{mol}\) = \(\text{1,99}\) \(\text{mol}\)
|
Previous
14.2 Nutrients
|
Table of Contents |
Next
14.4 The fertiliser industry
|