|
Previous
9.5 Applications of acids and bases
|
Next
10.1 Introduction
|
The Arrhenius definition of acids and bases defines an acid as a substance that increases the concentration of hydronium ions \((\text{H}_{3}\text{O}^{+})\) in a solution. A base is defined as a substance that increases the concentration of hydroxide ions \((\text{OH}^{-}\)) in a solution. However, this definition only applies to aqueous solutions (in water).
The Brønsted-Lowry definition is much broader. An acid is a substance that donates protons (\(\text{H}^{+}\)) and a base is a substance that accepts protons.
In different reactions, certain substances can act as both an acid and a base. These substances are amphoteric substances. Amphiprotic substances are amphoteric substances that are Brønsted-Lowry acids and bases. Water is both amphoteric and amphiprotic.
A conjugate acid-base pair refers to two compounds (one reactant and one product) that differ only by a hydrogen ion (\(\text{H}^{+}\)) and a charge of +1.
A large percentage of molecules in a strong acid or base dissociate or ionise to form ions in solution.
Only a small percentage of molecules in a weak acid or base dissociate or ionise to form ions in solution.
In a concentrated solution there is a high ratio of dissolved substance to solvent.
In a dilute solution there is a low ratio of dissolved substance to solvent.
\(\text{K}_{\text{a}}\) and \(\text{K}_{\text{b}}\) are the equilibrium constants for the reaction of an acid or a base with water. A large \(\text{K}_{\text{a}}\) or \(\text{K}_{\text{b}}\) means that the acid or base is strong. A small \(\text{K}_{\text{a}}\) or \(\text{K}_{\text{b}}\) means that the acid or base is weak.
When an acid and a base react, they form a salt and water. The salt is made up of a cation from the base and an anion from the acid. An example of a salt is sodium chloride \((\text{NaCl})\), which is the product of the reaction between sodium hydroxide \((\text{NaOH})\) and hydrochloric acid \((\text{HCl})\).
The reaction between an acid and a base is a neutralisation reaction.
In the reaction between an acid and a metal the products are a salt and hydrogen.
In the reaction between an acid and a metal hydroxide or metal oxide the products are a salt and water.
In the reaction between an acid and a metal carbontae or metal hydrogen carbonate the products are a salt, water and carbon dioxide.
The pH scale is a measure of the acidity or alkalinity of a solution. It ranges from \(\text{0}\) to \(\text{14}\). Values greater than \(\text{7}\) indicate a base, while those less than \(\text{7}\) indicate an acid.
Water ionises to a small extent. \(\textbf{K}_{\textbf{w}}\) is a measure of this auto-ionisation. \(\text{K}_{\text{w}}\) is \(\text{1} \times \text{10}^{-\text{14}}\) at \(\text{25}\) \(\text{℃}\).
An indicator is a compound that is a different colour in a basic solution, an acidic solution, and at the end-point of a reaction. They are used to determine the end-point during a neutralisation reaction.
Titrations are the method used to determine the concentration of a known substance using another, standard, solution. Acid-base titrations are an example.
Two notable applications of acids and bases are in the chloralkali industry, and in hair products including permanent waving applications, hair relaxers, and hair dyes.
The stomach secretes gastric juice, which contains hydrochloric acid. The gastric juice helps with digestion. Sometimes there is an overproduction of acid, leading to heartburn or indigestion. Antacids, such as milk of magnesia, can be taken to neutralise the excess acid. Milk of magnesia is only slightly soluble in water and has the chemical formula \(\text{Mg}(\text{OH})_{2}\).
Write a balanced chemical equation to show how the antacid reacts with the acid.
base + acid \(\to\) salt + water
The cation (from the base) is \(\text{Mg}^{2+}\). The anion (from the acid) is \(\text{Cl}^{-}\).
Therefore the salt is \(\text{MgCl}_{2}\)
\(\text{Mg}(\text{OH})_{2}(\text{s}) + 2\text{HCl}(\text{aq})\) \(\to\) \(\text{MgCl}_{2}(\text{aq}) + 2\text{H}_{2}\text{O}(\text{ℓ})\)
The instructions on the bottle recommend that children under the age of \(\text{12}\) years take one teaspoon of milk of magnesia, whereas adults can take two teaspoons of the antacid. Briefly explain why the dosages are different.
Adults have a bigger mass and generally produce more acid than children. Adults will therefore need more antacid to neutralise the excess acid. If children were to take the same dosage as adults they would have excess base in their stomach.
Why is it not advisable to take an overdose of the antacid? Refer to the hydrochloric acid concentration in the stomach in your answer.
(DoE Grade 11 Exemplar, 2007)
A low acid concentration (pH too high) in the stomach may slow down food digestion or may cause further stomach upset.
The compound \(\text{NaHCO}_{3}\) is commonly known as baking soda. A recipe requires \(\text{1,6}\) \(\text{g}\) of baking soda, mixed with other ingredients, to bake a cake.
Calculate the number of moles of \(\text{NaHCO}_{3}\) used to bake the cake.
\(M(\text{NaHCO}_{3}) = \text{23,0} + \text{1,01} + \text{12,0} + (\text{3} \times \text{16,0}) = \text{84,01} \text{g·mol$^{-1}$}\)
\(n(\text{NaHCO}_{3}) = \dfrac{m}{M} = \dfrac{\text{1,6}\text{ g}}{\text{84,01}\text{ g·mol$^{-1}$}} = \text{0,019} \text{ mol}\)
How many atoms of oxygen are there in \(\text{1,6}\) \(\text{g}\) of baking soda?
\(\text{N}_{\text{A}}\) (Avogadro's number) = \(\text{6,022} \times \text{10}^{\text{23}}\) \(\text{atoms·mol$^{-1}$}\).
Number of atoms = n x \(\text{N}_{\text{A}}\) = \(\text{0,019}\) \(\text{mol}\) x \(\text{6,022} \times \text{10}^{\text{23}}\) \(\text{atoms·mol$^{-1}$}\)
Number of atoms = \(\text{1,14} \times \text{10}^{\text{22}}\) atoms.
During the baking process, baking soda reacts with an acid (e.g. acetic acid in vinegar) to produce carbon dioxide and water, as shown by the reaction equation below:
\(\text{NaHCO}_{3}(\text{aq}) + \text{CH}_{3}\text{COOH}(\text{aq})\) \(\to\) \(\text{CH}_{3}\text{COONa}(\text{aq}) + \text{CO}_{2}(\text{g}) + \text{H}_{2}\text{O}(\text{ℓ})\)
Use the above equation to explain why the cake rises during this baking process.
(DoE Grade 11 Paper 2, 2007)
The carbon dioxide gas that is formed during the reaction forms bubbles in the cake mixture causing it to rise along with the expanding volume of the gas bubbles.
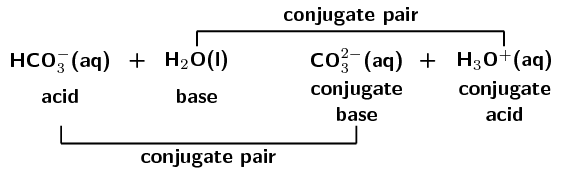
Label the acid-base conjugate pairs in the following equation:
\(\text{HCO}_{3}^{-}(\text{aq}) + \text{H}_{2}\text{O}(\text{ℓ})\) \(\rightleftharpoons\) \(\text{CO}_{3}^{2-}(\text{aq}) + \text{H}_{3}\text{O}^{+}(\text{aq})\)
A certain antacid tablet contains \(\text{22,0}\) \(\text{g}\) of baking soda \((\text{NaHCO}_{3})\). It is used to neutralise the excess hydrochloric acid in the stomach. The balanced equation for the reaction is:
\(\text{NaHCO}_{3}(\text{s}) + \text{HCl}(\text{aq})\) \(\to\) \(\text{NaCl}(\text{aq}) + \text{H}_{2}\text{O}(\text{ℓ}) + \text{CO}_{2}(\text{g})\)
The hydrochloric acid in the stomach has a concentration of \(\text{1,0}\) \(\text{mol·dm$^{-3}$}\). Calculate the volume of the hydrochloric acid that can be neutralised by the antacid tablet.
(DoE Grade 11 Paper 2, 2007)
\(M(\text{NaHCO}_{3}) = \text{23,0} + \text{1,01} + \text{12,0} + (\text{3} \times \text{16,0}) = \text{84,01} \text{ g·mol$^{-1}$}\)
\(n\text{(NaHCO}_{3}{\text{)}} = \dfrac{m}{M}\)
\(n = \dfrac{\text{22,0}\text{ g}}{\text{84,01}\text{ g·mol$^{-1}$}}\) = \(\text{0,26}\) \(\text{mol}\)
From the balanced equation we see that the molar ratio of \(\text{NaHCO}_{3}\) to \(\text{HCl}\) is \(\text{1}\):\(\text{1}\).
Therefore, \(n(\text{HCl}) = n(\text{NaHCO}_{3}) = \text{0,26} \text{ mol}\)
\(c = \dfrac{n}{V}\) therefore \(V = \dfrac{n}{c}\)
\(V\text{(HCl)} = \dfrac{\text{0,26}\text{ mol}}{\text{1,0}\text{ mol·dm$^{-3}$}}\) = \(\text{0,26}\) \(\text{dm$^{3}$}\)
A learner finds some sulfuric acid solution in a bottle labelled 'dilute sulfuric acid'. He wants to determine the concentration of the sulfuric acid solution. To do this, he decides to titrate the sulfuric acid against a standard potassium hydroxide (KOH) solution.
What is a standard solution?
A standard solution is a solution that contains a precisely known concentration of a substance. This substance can then be used in titrations.
Calculate the mass of \(\text{KOH}\) which he must use to make \(\text{300}\) \(\text{cm$^{3}$}\) of a \(\text{0,2}\) \(\text{mol·dm$^{-3}$}\) \(\text{KOH}\) solution.
\(V(\text{KOH}) = \text{300} \text{ cm$^{3}$} \times \dfrac{\text{0,001} {\text{ dm}}^{3}}{\text{1} {\text{ cm}}^{3}} = \text{0,3} \text{ dm$^{3}$}\)
\(C = \dfrac{n}{V}\), therefore \(n = C \times V\)
\(n(\text{KOH}) = \text{0,2} \text{ mol·dm$^{-3}$} \times \text{0,3} \text{ dm$^{3}$} = \text{0,06} \text{ mol}\)
\(M(\text{KOH}) = (\text{39,1} + \text{16,0} + \text{1,01}) \text{ g·mol$^{-1}$} = \text{56,11} \text{ g·mol$^{-1}$}\)
\(n = \dfrac{m}{M}\), therefore \(m = n \times M\)
\(m(\text{KOH}) = \text{0,06} \text{mol} \times \text{56,11} \text{ g·mol$^{-1}$} = \text{3,37} \text{ g}\)
Calculate the pH of the \(\text{0,2}\) \(\text{mol·dm$^{-3}$}\) \(\text{KOH}\) solution (assume standard temperature).
\(\text{KOH}\) is a very strong base and will completely dissociate in water. Therefore the concentration of \(\text{OH}^{-}\) ions is the same as the concentration of the solution.
pH is defined as: pH = -log\([\text{H}^{+}]\)
However, we can also define pOH in a similar way: pOH = -log\([\text{OH}^{-}]\)
The relationship between the two is: 14 = pH + pOH, therefore pH = 14 - pOH
pH = \(\text{14}\) - (-log\([\text{OH}^{-}]\)) = \(\text{14}\) - (-log[\(\text{0,2}\)]) = \(\text{14}\) - \(\text{0,7}\) = \(\text{13,3}\)
Write a balanced chemical equation for the reaction between \(\text{H}_{2}\text{SO}_{4}\) and \(\text{KOH}\).
Sulfuric acid is a strong acid and potassium hydroxide is a strong base, therefore the equation is:
\(\text{H}_{2}\text{SO}_{4}(\text{aq}) + 2\text{KOH}(\text{aq})\) \(\to\) \(\text{K}_{2}\text{SO}_{4}(\text{aq}) + 2\text{H}_{2}\text{O}(\text{ℓ})\)
During the titration the learner finds that \(\text{15}\) \(\text{cm$^{3}$}\) of the KOH solution neutralises \(\text{20}\) \(\text{cm$^{3}$}\) of the \(\text{H}_{2}\text{SO}_{4}\) solution. Calculate the concentration of the \(\text{H}_{2}\text{SO}_{4}\) solution.
(IEB Paper 2, 2003)
\(V(\text{KOH}) = \text{15} \text{ cm$^{3}$} \times \dfrac{\text{0,001} {\text{ dm}}^{3}}{\text{1} {\text{ cm}}^{3}} = \text{0,015} \text{ dm$^{3}$}\)
The number of moles of \(\text{KOH}\) used to neutralise the \(\text{H}_{2}\text{SO}_{4}\) is:
\(n(\text{KOH}) = c \times V = \text{0,2} \text{ mol·dm$^{-3}$} \times \text{0,015} \text{ dm$^{3}$} = \text{0,003} \text{ mol}\)
From the balanced equation we see that the mole ratio of \(\text{H}_{2}\text{SO}_{4}\) to \(\text{KOH}\) is \(\text{1}\):\(\text{2}\). There is one mole of sulfuric acid for every two moles of potassium hydroxide.
\(n(\text{H}_{2}\text{SO}_{4}) = \dfrac{\text{0,003}\text{ mol}}{\text{2}} = \text{0,0015} \text{ mol}\)
\(V(\text{H}_{2}\text{SO}_{4}) = \text{20} \text{ cm$^{3}$} \times \dfrac{\text{0,001} {\text{ dm}}^{3}}{\text{1} {\text{ cm}}^{3}} = \text{0,020} \text{ dm$^{3}$}\)
Therefore, the concentration of the sulfuric acid is:
\(c(\text{H}_{2}\text{SO}_{4}) = \dfrac{n}{V} = \dfrac{\text{0,0015}\text{ mol}}{\text{0,020}\text{ dm$^{3}$}} = \text{0,075} \text{ mol·dm$^{-3}$}\)
|
Previous
9.5 Applications of acids and bases
|
Table of Contents |
Next
10.1 Introduction
|
