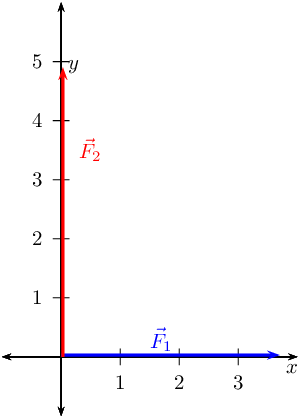
Draw the following forces as vectors on the Cartesian plane originating at
the origin:
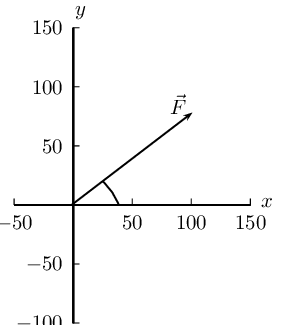
- \(\vec{F}_{1} = \text{3,7}\text{ N}\) in the positive
\(x\)-direction
- \(\vec{F}_{2} = \text{4,9}\text{ N}\) in the positive
\(y\)-direction
We choose a scale of \(\text{1}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\).
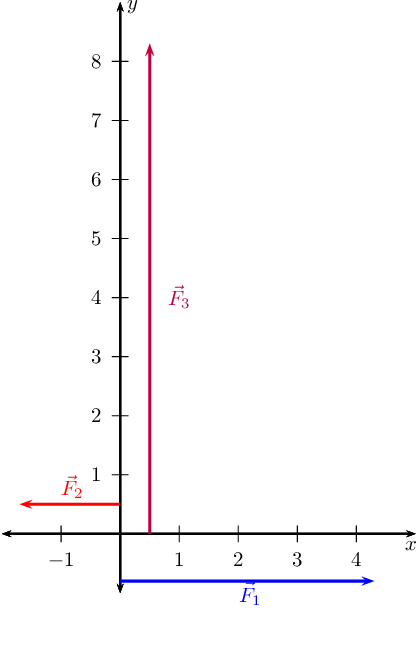
Draw the following forces as vectors on the Cartesian plane:
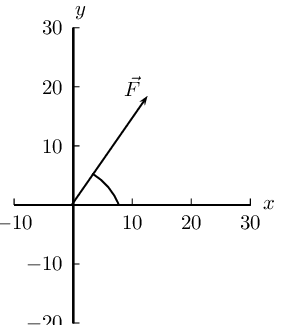
- \(\vec{F}_{1} = \text{4,3}\text{ N}\) in the positive
\(x\)-direction
- \(\vec{F}_{2} = \text{1,7}\text{ N}\) in the negative
\(x\)-direction
- \(\vec{F}_{3} = \text{8,3}\text{ N}\) in the positive
\(y\)-direction
We choose a scale of \(\text{1}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\).
Find the resultant in the \(x\)-direction, \(R_x\), and \(y\)-direction,
\(R_y\) for the following forces:
- \(\vec{F}_{1} = \text{1,5}\text{ N}\) in the positive
\(x\)-direction
- \(\vec{F}_{2} = \text{1,5}\text{ N}\) in the positive
\(x\)-direction
- \(\vec{F}_{3} = \text{2}\text{ N}\) in the negative \(x\)-direction
We choose a scale of \(\text{1}\) \(\text{N}\): \(\text{1}\) \(\text{cm}\)
and for our diagram we will define the positive direction as to the
right.
We note that there are no vectors in the \(y\)-direction and so \(R_{y} =
0\).
We now find \(\vec{R}_{x}\):
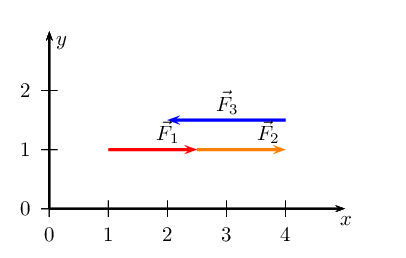
We have now drawn all the force vectors that act in the \(x\)-direction. To
find \(\vec{R}_{x}\) we note that the resultant vector is the arrow
which starts at the tail of the first vector and ends at the head of the
last drawn vector in that direction.
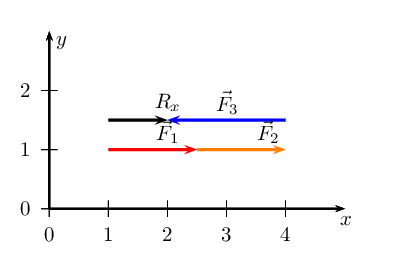
We note that \(\vec{R}_{x}\) is \(\text{1}\) \(\text{cm}\) or \(\text{1}\)
\(\text{N}\) in the positive \(x\)-direction.
\(\vec{R}_{x}\) = \(\text{1}\) \(\text{N}\) and points in the positive
\(x\)-direction. \(\vec{R}_{y}\) = \(\text{0}\) \(\text{N}\).
Find the resultant in the \(x\)-direction, \(R_x\), and \(y\)-direction,
\(R_y\) for the following forces:
- \(\vec{F}_{1} = \text{4,8}\text{ N}\) in the positive
\(x\)-direction
- \(\vec{F}_{2} = \text{3,2}\text{ N}\) in the negative
\(x\)-direction
- \(\vec{F}_{3} = \text{1,9}\text{ N}\) in the positive
\(y\)-direction
- \(\vec{F}_{4} = \text{2,1}\text{ N}\) in the negative
\(y\)-direction
We choose a scale of \(\text{1}\) \(\text{N}\): \(\text{1}\) \(\text{cm}\)
and for our diagram we will define the positive direction as to the
right.
We find \(\vec{R}_{x}\):
We have now drawn all the force vectors that act in the \(x\)-direction. To
find \(\vec{R}_{x}\) we note that the resultant vector is the arrow
which starts at the tail of the first vector and ends at the head of the
last drawn vector in that direction.
We note that \(\vec{R}_{x}\) is \(\text{1,6}\) \(\text{cm}\) or
\(\text{1,6}\) \(\text{N}\) in the positive \(x\)-direction.
We now find \(\vec{R}_{y}\):
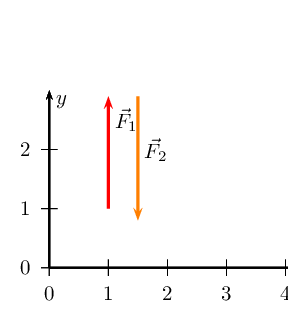
We have now drawn all the force vectors that act in the \(x\)-direction. To
find \(\vec{R}_{x}\) we note that the resultant vector is the arrow
which starts at the tail of the first vector and ends at the head of the
last drawn vector in that direction.
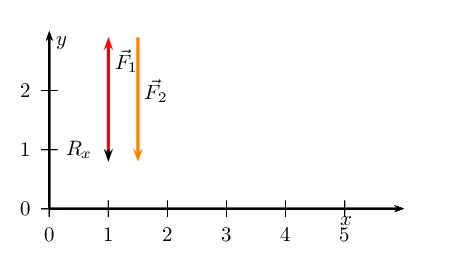
We note that \(\vec{R}_{y}\) is \(\text{0,2}\) \(\text{cm}\) or
\(\text{0,2}\) \(\text{N}\) in the negative \(y\)-direction.
\(\vec{R}_{x}\) = \(\text{1,6}\) \(\text{N}\) and points in the positive
\(x\)-direction. \(\vec{R}_{y}\) = \(\text{0,2}\) \(\text{N}\) and
points in the negative \(y\)-direction.
Find the resultant in the \(x\)-direction, \(R_x\), and \(y\)-direction,
\(R_y\) for the following forces:
- \(\vec{F}_{1} = \text{2,7}\text{ N}\) in the positive
\(x\)-direction
- \(\vec{F}_{2} = \text{1,4}\text{ N}\) in the positive
\(x\)-direction
- \(\vec{F}_{3} = \text{2,7}\text{ N}\) in the negative
\(x\)-direction
- \(\vec{F}_{4} = \text{1,7}\text{ N}\) in the negative
\(y\)-direction
We choose a scale of \(\text{1}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\)
and for our diagram we will define the positive direction as to the
right.
We find \(\vec{R}_{x}\):
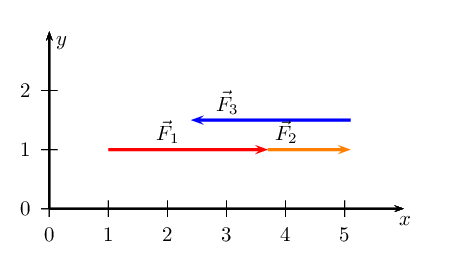
We have now drawn all the force vectors that act in the \(x\)-direction. To
find \(\vec{R}_{x}\) we note that the resultant vector is the arrow
which starts at the tail of the first vector and ends at the head of the
last drawn vector in that direction.
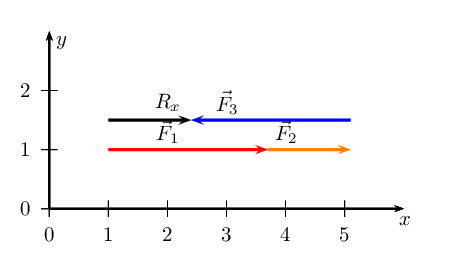
We note that \(\vec{R}_{x}\) is \(\text{1,4}\) \(\text{cm}\) or
\(\text{1,4}\) \(\text{N}\) in the positive \(x\)-direction.
There is only one vector in the \(y\)-direction and so this is
\(\vec{R}_{y}\).
\(\vec{R}_{x}\) = \(\text{1,4}\) \(\text{N}\) and points in the positive
\(x\)-direction. \(\vec{R}_{y}\) = \(\text{1,7}\) \(\text{N}\) and
points in the negative \(y\)-direction.
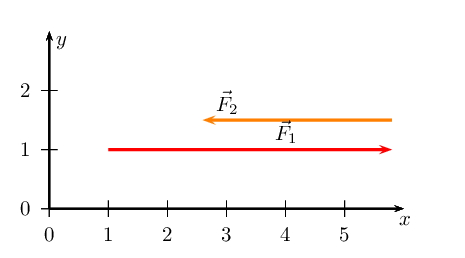
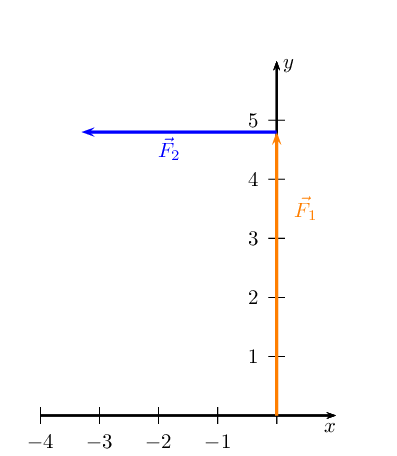
Sketch the resultant of the following force vectors using the tail-to-head
method:
- \(\vec{F}_{1} = \text{4,8}\text{ N}\) in the positive
\(y\)-direction
- \(\vec{F}_{2} = \text{3,3}\text{ N}\) in the negative
\(x\)-direction
We first sketch the vectors on the Cartesian plane. We choose a scale of
\(\text{1}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\). Remember to
sketch \(F_{2}\) starting at the head of \(F_{1}\).
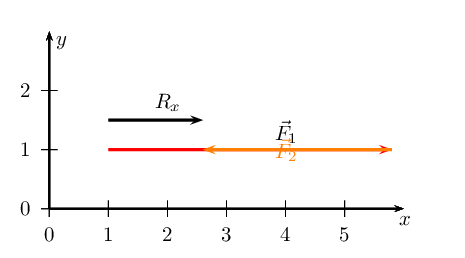
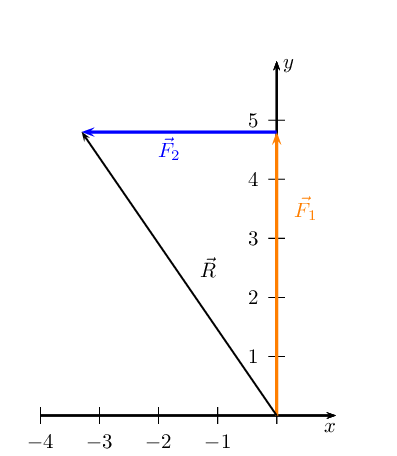
The resultant, \(\vec{R}\), is the vector connecting the tail of the first
vector drawn to the head of the last vector drawn:
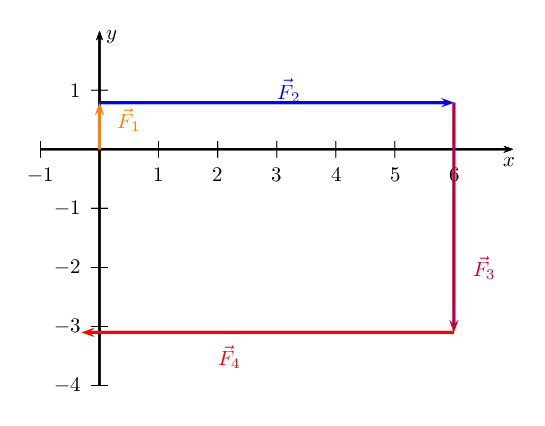
Sketch the resultant of the following force vectors using the tail-to-head
method:
- \(\vec{F}_{1} = \text{0,7}\text{ N}\) in the positive
\(y\)-direction
- \(\vec{F}_{2} = \text{6}\text{ N}\) in the positive \(x\)-direction
- \(\vec{F}_{3} = \text{3,8}\text{ N}\) in the negative
\(y\)-direction
- \(\vec{F}_{4} = \text{11,9}\text{ N}\) in the negative
\(x\)-direction
We first sketch the vectors on the Cartesian plane. We choose a scale of
\(\text{1}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\). Remember to
sketch \(F_{2}\) starting at the head of \(F_{1}\).
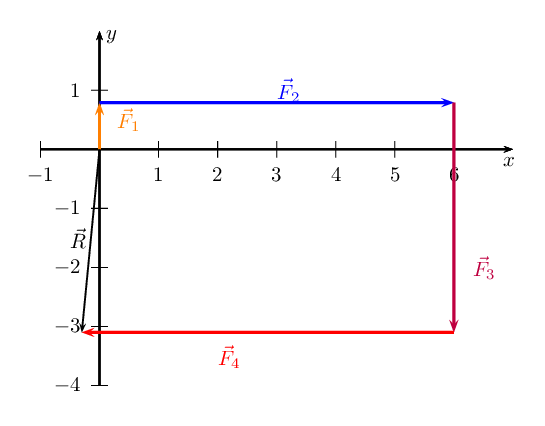
The resultant, \(\vec{R}\), is the vector connecting the tail of the first
vector drawn to the head of the last vector drawn:
Sketch the resultant of the following force vectors using the tail-to-head
method by first determining the resultant in the \(x\)- and
\(y\)-directions:
- \(\vec{F}_{1} = \text{5,2}\text{ N}\) in the positive
\(y\)-direction
- \(\vec{F}_{2} = \text{7,5}\text{ N}\) in the negative
\(y\)-direction
- \(\vec{F}_{3} = \text{4,8}\text{ N}\) in the positive
\(y\)-direction
- \(\vec{F}_{4} = \text{6,3}\text{ N}\) in the negative
\(x\)-direction
We choose a scale of \(\text{2}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\).
We first determine \(\vec{R}_{x}\)
Draw the Cartesian plane with the vectors in the \(x\)-direction:
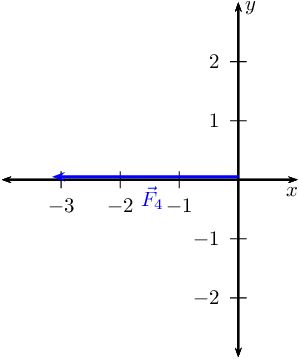
This is \(\vec{R}_{x}\) since it is the only vector in the \(x\)-direction.
Secondly determine \(\vec{R}_{y}\)
Next we draw the Cartesian plane with the vectors in the \(y\)-direction:
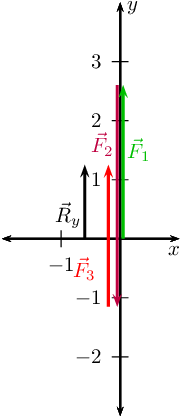
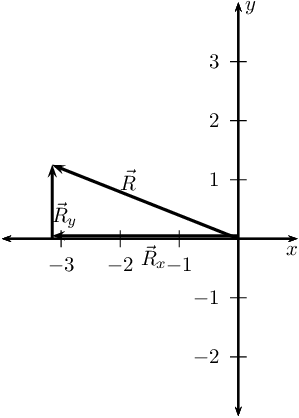
Now we draw the resultant vectors, \(\vec{R}_{y}\) and \(\vec{R}_{x}\)
head-to-tail:
Sketch the resultant of the following force vectors using the tail-to-head
method by first determining the resultant in the \(x\)- and
\(y\)-directions:
- \(\vec{F}_{1} = \text{6,7}\text{ N}\) in the positive
\(y\)-direction
- \(\vec{F}_{2} = \text{4,2}\text{ N}\) in the negative
\(x\)-direction
- \(\vec{F}_{3} = \text{9,9}\text{ N}\) in the negative
\(y\)-direction
- \(\vec{F}_{4} = \text{3,4}\text{ N}\) in the negative
\(y\)-direction
We choose a scale of \(\text{1}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\).
We first determine \(\vec{R}_{x}\)
Draw the Cartesian plane with the vectors in the \(x\)-direction:
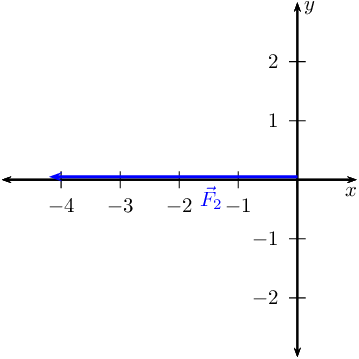
This is \(\vec{R}_{x}\) since it is the only vector in the \(x\)-direction.
Secondly determine \(\vec{R}_{y}\)
Next we draw the Cartesian plane with the vectors in the \(y\)-direction:
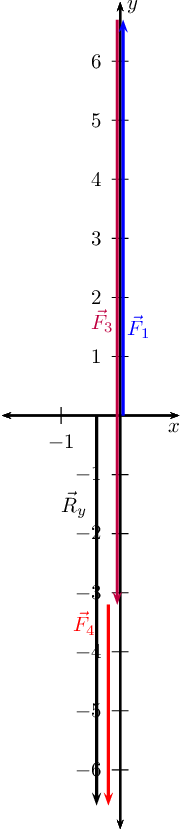
Now we draw the resultant vector, \(\vec{R}_{y}\) and \(\vec{R}_{x}\)
head-to-tail:
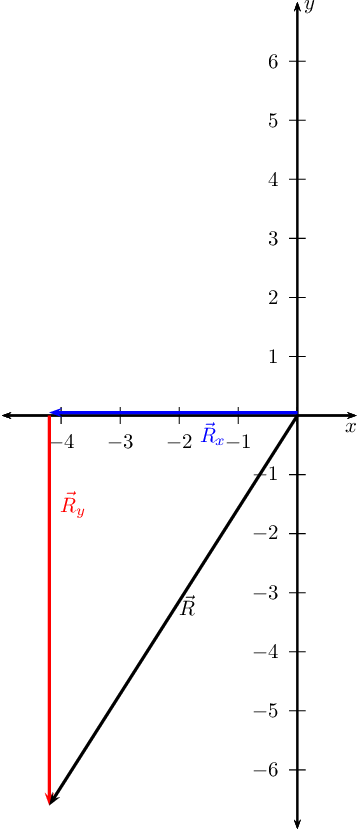
Sketch the resultant of the following force vectors using the tail-to-tail
method:
- \(\vec{F}_{1} = \text{6,1}\text{ N}\) in the positive
\(y\)-direction
- \(\vec{F}_{2} = \text{4,5}\text{ N}\) in the negative
\(x\)-direction
We first draw a Cartesian plane with the two vectors: (we use a scale of
\(\text{1}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\))
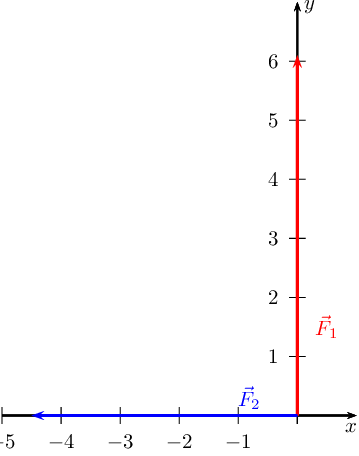
Now we draw a line parallel to \(\vec{F}_{1}\) from the head of
\(\vec{F}_{2}\) and we draw a line parallel to \(\vec{F}_{2}\) from the
head of \(\vec{F}_{1}\):
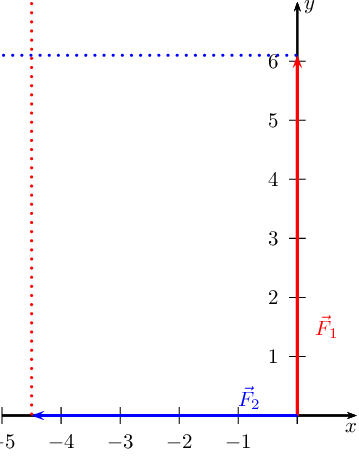
Where the two lines intersect is the head of the resultant vector which will
originate at the origin so:
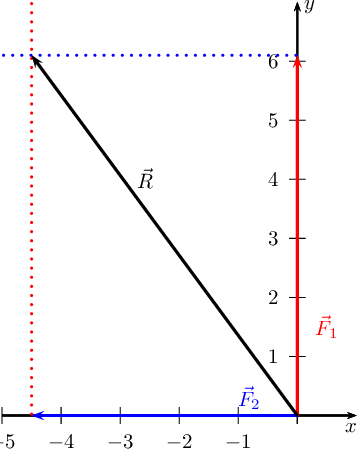
Sketch the resultant of the following force vectors using the tail-to-tail
method by first determining the resultant in the \(x\)- and
\(y\)-directions:
- \(\vec{F}_{1} = \text{2,3}\text{ N}\) in the positive
\(y\)-direction
- \(\vec{F}_{2} = \text{11,8}\text{ N}\) in the negative
\(y\)-direction
- \(\vec{F}_{3} = \text{7,9}\text{ N}\) in the negative
\(y\)-direction
- \(\vec{F}_{4} = \text{3,2}\text{ N}\) in the negative
\(x\)-direction
We need to determine \(\vec{R}_{x}\) and \(\vec{R}_{y}\) and then use these
to find the resultant.
Determine \(\vec{R}_{x}\). We choose a scale of \(\text{2}\) \(\text{N}\) :
\(\text{1}\) \(\text{cm}\).
Draw the Cartesian plane with the vectors in the \(x\)-direction:
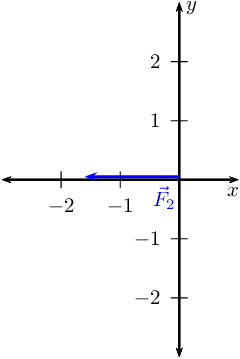
This is \(\vec{R}_{x}\) since it is the only vector in the \(x\)-direction.
Secondly determine \(\vec{R}_{y}\)
Next we draw the Cartesian plane with the vectors in the \(y\)-direction:
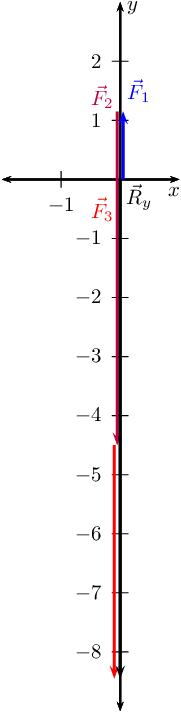
Now we draw the resultant vectors, \(\vec{R}_{y}\) and \(\vec{R}_{x}\)
tail-to-tail:

Now we can draw the lines to show us where the head of the resultant must be:
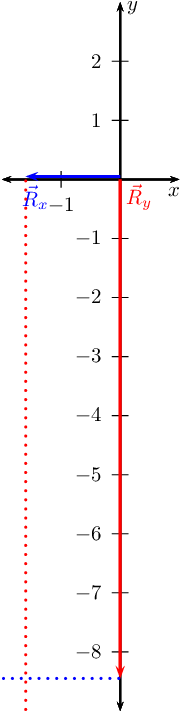
And finally we find the resultant:
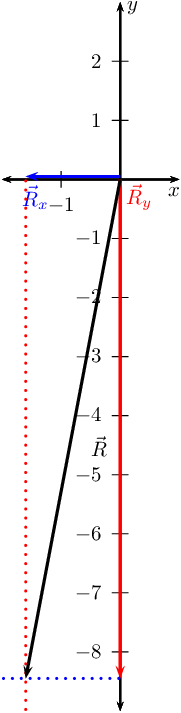
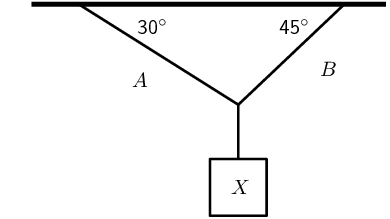
Four forces act simultaneously at a point, find the resultant if the forces
are:
-
\(\vec{F}_{1}\) = \(\text{2,3}\) \(\text{N}\) in the positive
\(x\)-direction
-
\(\vec{F}_{2}\) = \(\text{4,9}\) \(\text{N}\) in the positive
\(y\)-direction
-
\(\vec{F}_{3}\) = \(\text{4,3}\) \(\text{N}\) in the negative
\(y\)-direction
-
\(\vec{F}_{4}\) = \(\text{3,1}\) \(\text{N}\) in the negative
\(y\)-direction
We note that we have more than two vectors so we must first find the
resultant in the \(x\)-direction and the resultant in the
\(y\)-direction.
In the \(x\)-direction we only have one vector and so this is the resultant.
In the \(y\)-direction we have three vectors. We can add these algebraically
to find \(\vec{R}_{y}\):
\begin{align*}
\vec{F}_{2} & = \text{+4,9}\text{ N} \\
\vec{F}_{3} & = -\text{4,3}\text{ N} \\
\vec{F}_{4} & = -\text{3,1}\text{ N}
\end{align*}
Thus, the resultant force is:
\begin{align*}
\vec{F}_{2} + \vec{F}_{3} + \vec{F}_{4} & = (\text{4,9}) + (-\text{4,3}) +
(-\text{3,1}) \\
& = -\text{2,3}
\end{align*}
Now we use \(\vec{R}_{x}\) and \(\vec{R}_{y}\) to find the resultant.
We note that the triangle formed by \(\vec{R}_{x}\), \(\vec{R}_{y}\) and the
resultant vector is a right-angle triangle. We can thus use the Theorem
of Pythagoras to determine the length of the resultant. Let \(R\)
represent the length of the resultant vector. Then:
\begin{align*}
F_x^{2} + F_y^{2} &= R^{2}\ \text{Pythagoras' theorem}\\
(\text{2,3})^{2} + (-\text{2,3})^{2} &= R^{2}\\
R &= \text{3,25}\text{ N}
\end{align*}
To determine the direction of the resultant force, we calculate the angle
α between the resultant force vector and the positive \(x\)-axis,
by using simple trigonometry:
\begin{align*}
\tan\alpha &= \frac{\text{opposite side}}{\text{adjacent side}} \\
\tan\alpha &= \frac{\text{2,3}}{\text{2,3}} \\
\alpha &= \tan^{-1}(\text{1}) \\
\alpha &= \text{45}\text{°}
\end{align*}
The resultant force is then \(\text{3,25}\) \(\text{N}\) at
\(\text{45}\)\(\text{°}\) to the \(x\)-axis.
A point is acted on by two forces and the resultant is zero. The forces
-
have equal magnitudes and directions.
-
have equal magnitudes but opposite directions.
-
act perpendicular to each other.
-
act in the same direction.
have equal magnitudes but opposite directions.
A point in equilibrium is acted on by three forces. Force \(F_{1}\) has
components \(\text{15}\) \(\text{N}\) due south and \(\text{13}\)
\(\text{N}\) due west. What are the components of force \(F_{2}\)?
-
\(\text{13}\) \(\text{N}\) due north and \(\text{20}\)
\(\text{N}\) due west
-
\(\text{13}\) \(\text{N}\) due north and \(\text{13}\)
\(\text{N}\) due west
-
\(\text{15}\) \(\text{N}\) due north and \(\text{7}\)
\(\text{N}\) due west
-
\(\text{15}\) \(\text{N}\) due north and \(\text{13}\)
\(\text{N}\) due east
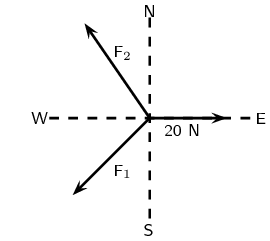
\(\text{15}\) \(\text{N}\) due north and \(\text{7}\) \(\text{N}\) due west
Two vectors act on the same point. What should the angle between them be so
that a maximum resultant is obtained?
-
\(\text{0}\)\(\text{°}\)
-
\(\text{90}\)\(\text{°}\)
-
\(\text{180}\)\(\text{°}\)
-
cannot tell
Two forces, \(\text{4}\) \(\text{N}\) and \(\text{11}\) \(\text{N}\), act on
a point. Which one of the following cannot be the magnitude of a
resultant?
-
\(\text{4}\) \(\text{N}\)
-
\(\text{7}\) \(\text{N}\)
-
\(\text{11}\) \(\text{N}\)
-
\(\text{15}\) \(\text{N}\)
\(\text{4}\) \(\text{N}\)
An object of weight W is supported by two cables attached to the ceiling and
wall as shown. The tensions in the two cables are \(T_{1}\) and
\(T_{2}\) respectively. Tension \(T_{1} = \text{1 200}\text{ N}\).
Determine the tension \(T_{2}\) by accurate construction and measurement
or by calculation.
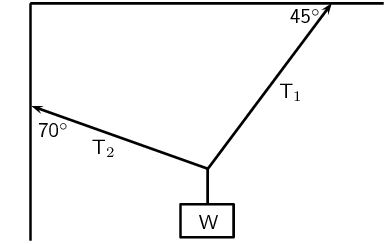
We will use the \(x\)-component of \(T_{2}\) the fact that \(T_{1x} =
T_{2x}\) to find \(T_{2}\):
\begin{align*}
T_{2x} & = T_{1x} \\
T_{2} \cos(\text{20}\text{°}) & = T_{1}\cos(\text{45}\text{°})\\
T_{2} \cos(\text{20}\text{°}) & =
(\text{1 200})(\cos(\text{45}\text{°})) \\
T_{2} \cos(\text{20}\text{°}) & = \text{848,53} \\
T_{2} & = \text{902,98}\text{ N}
\end{align*}