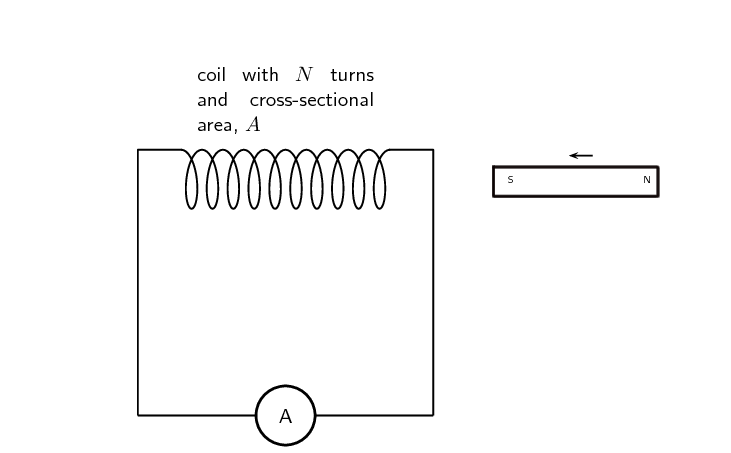10.3 Faraday's law of electromagnetic induction (ESBPY)
Current induced by a changing magnetic field (ESBPZ)
While Oersted's surprising discovery of electromagnetism paved the way for more practical applications of
electricity, it was Michael Faraday who gave us the key to the practical generation of electricity:
electromagnetic induction.
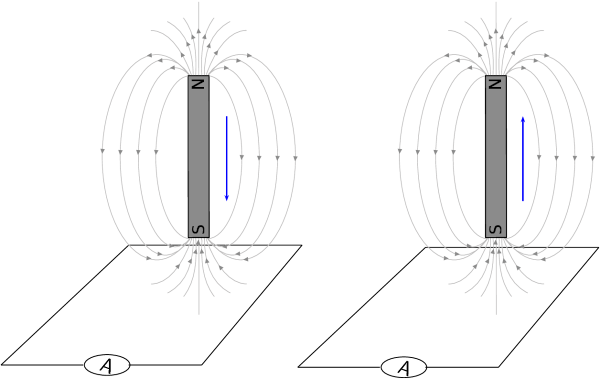
Faraday discovered that when he moved a magnet near a wire a voltage was generated across it. If the magnet was
held stationary no voltage was generated, the voltage only existed while the magnet was moving. We call this
voltage the induced emf (\(\mathcal{E}\)).
A circuit loop connected to a sensitive ammeter will register a current if it is set up as in this figure and
the magnet is moved up and down:
Magnetic flux
Before we move onto the definition of Faraday's law of electromagnetic induction and examples, we first need
to spend some time looking at the magnetic flux. For a loop of area \(A\) in the presence of a uniform
magnetic field, \(\vec{B}\), the magnetic flux (\(φ\)) is defined as:
\[\phi = BA\cos\theta\]
Where:
\begin{align*}
\theta & = \text{the angle between the magnetic field, B, and the normal to the loop of area A}\\
A & = \text{the area of the loop}\\
B & = \text{the magnetic field}
\end{align*}
The S.I. unit of magnetic flux is the weber (Wb).
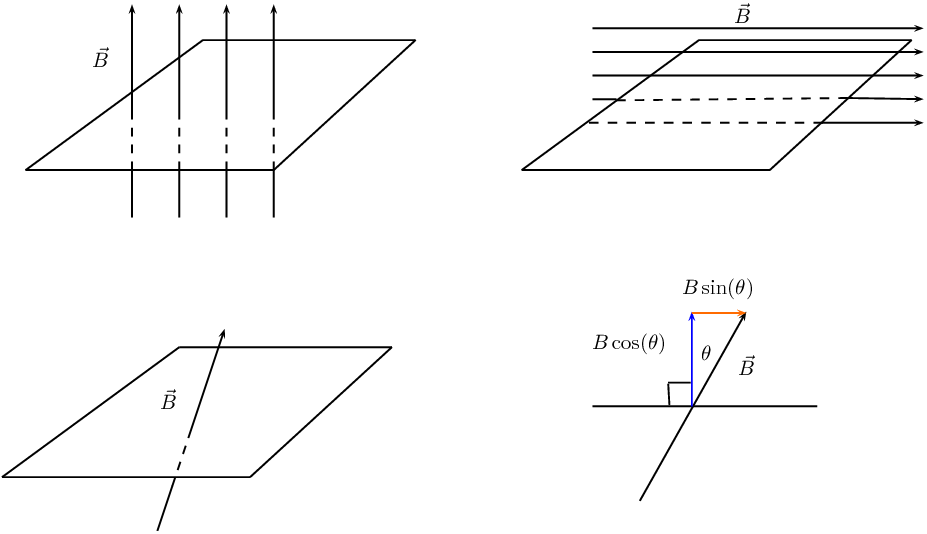
You might ask yourself why the angle \(\theta\) is included. The flux depends on the magnetic field that
passes through surface. We know that a field parallel to the surface can't induce a current because it doesn't
pass through the surface. If the magnetic field is not perpendicular to the surface then there is a component
which is perpendicular and a component which is parallel to the surface. The parallel component can't
contribute to the flux, only the vertical component can.
In this diagram we show that a magnetic field at an angle other than perpendicular can be broken into
components. The component perpendicular to the surface has the magnitude \(B\cos(\theta)\) where \(\theta\) is
the angle between the normal and the magnetic field.
- Faraday's Law of electromagnetic induction
-
The emf, \(\mathcal{E}\), produced around a loop of conductor is proportional to the rate of change of the
magnetic flux, φ, through the area, A, of the loop. This can be stated mathematically as:
\[\mathcal{E} = -N\frac{\Delta\phi}{\Delta t}\]
where \(\phi =B·A\) and B is the strength of the magnetic field. \(N\) is the number of circuit loops.
A magnetic field is measured in units of teslas (T). The minus sign indicates direction and that the induced
emf tends to oppose the change in the magnetic flux. The minus sign can be ignored when calculating
magnitudes.
Faraday's Law relates induced emf to the rate of change of flux, which is the product of the magnetic field and
the cross-sectional area through which the field lines pass.
It is not the area of the wire itself but the area that the wire encloses. This means that if you bend the
wire into a circle, the area we would use in a flux calculation is the surface area of the circle, not the
wire.
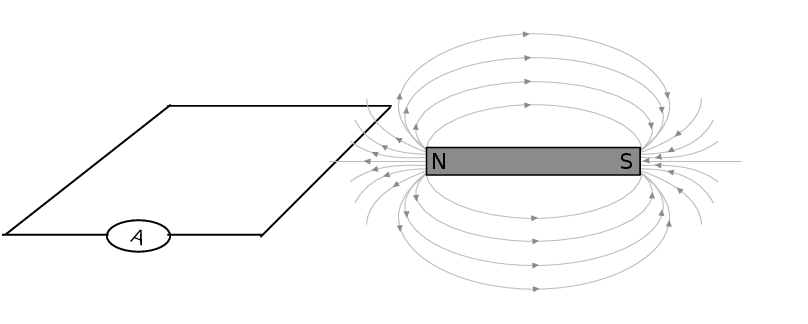
In this illustration, where the magnet is in the same plane as the circuit loop, there would be no current even
if the magnet were moved closer and further away. This is because the magnetic field lines do not pass through
the enclosed area but are parallel to it. The magnetic field lines must pass through the area enclosed by the
circuit loop for an emf to be induced.
Direction of induced current (ESBQ2)
The most important thing to remember is that the induced current opposes whatever change is taking place.
In the first picture (left) the circuit loop has the south pole of a magnet moving closer. The magnitude of the
field from the magnet is getting larger. The response from the induced emf will be to try to resist the field
towards the pole getting stronger. The field is a vector so the current will flow in a direction so that the
fields due to the current tend to cancel those from the magnet, keeping the resultant field the same.
To resist the change from an approaching south pole from above, the current must result in field lines that
move away from the approaching pole. The induced magnetic field must therefore have field lines that go down on
the inside of the loop. The current direction indicated by the arrows on the circuit loop will achieve this.
Test this by using the Right Hand Rule. Put your right thumb in the direction of one of the arrows and notice
that the field curls downwards into the area enclosed by the loop.
In the second diagram the south pole is moving away. This means that the field from the magnet will be getting
weaker. The response from the induced current will be to set up a magnetic field that adds to the existing one
from the magnetic to resist it decreasing in strength.
Another way to think of the same feature is just using poles. To resist an approaching south pole the current
that is induced creates a field that looks like another south pole on the side of the approaching south pole.
Like poles repel, you can think of the current setting up a south pole to repel the approaching south pole. In
the second panel, the current sets up a north pole to attract the south pole to stop it moving away.
We can also use the variation of the Right Hand Rule, putting your fingers in the direction of the current to
get your thumb to point in the direction of the field lines (or the north pole).
We can test all of these on the cases of a north pole moving closer or further away from the circuit. For the
first case of the north pole approaching, the current will resist the change by setting up a field in the
opposite direction to the field from the magnet that is getting stronger. Use the Right Hand Rule to confirm
that the arrows create a field with field lines that curl upwards in the enclosed area cancelling out those
curling downwards from the north pole of the magnet.
Like poles repel, alternatively test that putting the fingers of your right hand in the direction of the
current leaves your thumb pointing upwards indicating a north pole.

For the second figure where the north pole is moving away the situation is reversed.
Direction of induced current in a solenoid (ESBQ3)
The approach for looking at the direction of current in a solenoid is the same the approach described above.
The only difference being that in a solenoid there are a number of loops of wire so the magnitude of the induced
emf will be different. The flux would be calculated using the surface area of the solenoid multiplied by the
number of loops.
Remember: the directions of currents and associated magnetic fields can all be found using
only the Right Hand Rule. When the fingers of the right hand are pointed in the direction of the magnetic field,
the thumb points in the direction of the current. When the thumb is pointed in the direction of the magnetic
field, the fingers point in the direction of the current.
The direction of the current will be such as to oppose the change. We would use a setup as in this sketch to do
the test:

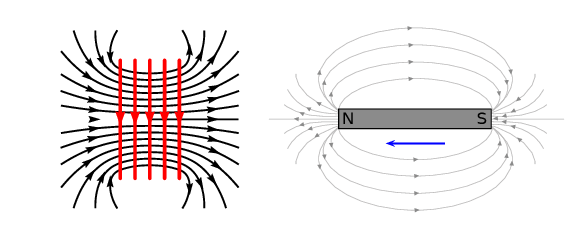
In the case where a north pole is brought towards the solenoid the current will flow so that a north pole is
established at the end of the solenoid closest to the approaching magnet to repel it (verify using the Right
Hand Rule):
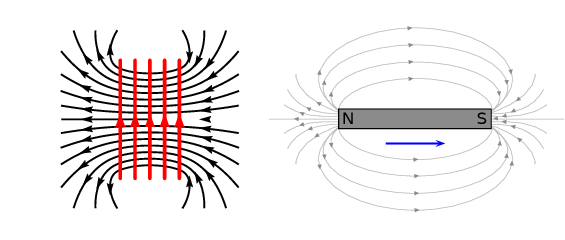
In the case where a north pole is moving away from the solenoid the current will flow so that a south pole is
established at the end of the solenoid closest to the receding magnet to attract it:
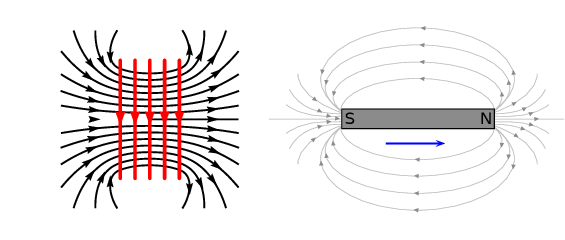
In the case where a south pole is moving away from the solenoid the current will flow so that a north pole is
established at the end of the solenoid closest to the receding magnet to attract it:
In the case where a south pole is brought towards the solenoid the current will flow so that a south pole is
established at the end of the solenoid closest to the approaching magnet to repel it:
An easy way to create a magnetic field of changing intensity is to move a permanent magnet next to a wire or
coil of wire. The magnetic field must increase or decrease in intensity perpendicular to the wire (so
that the magnetic field lines “cut across” the conductor), or else no voltage will be induced.
The induced current generates a magnetic field. The induced magnetic field is in a direction that tends to
cancel out the change in the magnetic field in the loop of wire. So, you can use the Right Hand Rule to find
the direction of the induced current by remembering that the induced magnetic field is opposite in direction
to the change in the magnetic field.
Induction
Electromagnetic induction is put into practical use in the construction of electrical generators which use
mechanical power to move a magnetic field past coils of wire to generate voltage. However, this is by no means
the only practical use for this principle.
If we recall, the magnetic field produced by a current-carrying wire is always perpendicular to the wire, and
that the flux intensity of this magnetic field varies with the amount of current which passes through it. We
can therefore see that a wire is capable of inducing a voltage along its own length if the current is
changing. This effect is called self-induction. Self-induction is when a changing magnetic field is
produced by changes in current through a wire, inducing a voltage along the length of that same wire.
If the magnetic flux is enhanced by bending the wire into the shape of a coil, and/or wrapping that coil
around a material of high permeability, this effect of self-induced voltage will be more intense. A device
constructed to take advantage of this effect is called an inductor.
Remember that the induced current will create a magnetic field that opposes the change in the magnetic flux.
This is known as Lenz's law.
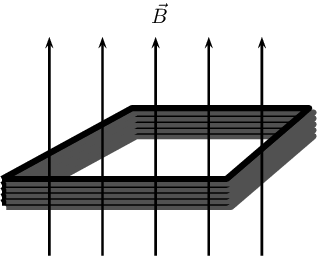
Worked example 1: Faraday's law
Consider a flat square coil with 5 turns. The coil is \(\text{0,50}\) \(\text{m}\) on each side and has a
magnetic field of \(\text{0,5}\) \(\text{T}\) passing through it. The plane of the coil is perpendicular to
the magnetic field: the field points out of the page. Use Faraday's Law to calculate the induced emf, if the
magnetic field is increases uniformly from \(\text{0,5}\) \(\text{T}\) to \(\text{1}\) \(\text{T}\) in
\(\text{10}\) \(\text{s}\). Determine the direction of the induced current.
Identify what is required
We are required to use
Faraday's Law to calculate the induced emf.
Write Faraday's Law
\[\mathcal{E}=-N\frac{\Delta\phi}{\Delta t}\]
We know that the magnetic field is at right angles to the surface and so aligned with the normal. This means
we do not need to worry about the angle that the field makes with the normal and \(\phi=BA\). The starting
or initial magnetic field, \(B_i\), is given as is the final field magnitude, \(B_f\). We want to determine
the magnitude of the emf so we can ignore the minus sign.
The area, \(A\), is the area of square coil.
Solve Problem
\begin{align*}
\mathcal{E}&=N\frac{\Delta\phi}{\Delta t}\\
&=N\frac{\phi_f-\phi_i}{\Delta t} \\
&=N\frac{B_fA - B_iA}{\Delta t} \\
&=N\frac{A(B_f - B_i)}{\Delta t} \\
&=(5)\frac{(\text{0,50})^2(\text{1} - \text{0,50})}{\text{10}} \\
&=(5)\frac{(\text{0,50})^2(\text{1} - \text{0,50})}{\text{10}} \\
&=\text{0,0625}\text{ V}
\end{align*}
The induced current is anti-clockwise as viewed from the direction of the increasing magnetic field.
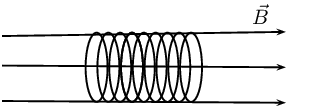
Worked example 2: Faraday's law
Consider a solenoid of 9 turns with unknown radius, \(r\). The solenoid is subjected to a magnetic field of
\(\text{0,12}\) \(\text{T}\). The axis of the solenoid is parallel to the magnetic field. When the field is
uniformly switched to \(\text{12}\) \(\text{T}\) over a period of 2 minutes an emf with a magnitude of
\(-\text{0,3}\) \(\text{V}\) is induced.
Determine the radius of the solenoid.
Identify what is required
We are required to determine the radius of the solenoid. We know that the relationship between the induced
emf and the field is governed by Faraday's law which includes the geometry of the solenoid. We can use this
relationship to find the radius.
Write Faraday's Law
\[\mathcal{E}=-N\frac{\Delta\phi}{\Delta t}\]
We know that the magnetic field is at right angles to the surface and so aligned with the normal. This means
we do not need to worry about the angle the field makes with the normal and \(\phi=BA\). The starting or
initial magnetic field, \(B_i\), is given as is the final field magnitude, \(B_f\). We can drop the minus
sign because we are working with the magnitude of the emf only.
The area, \(A\), is the surface area of the solenoid which is \(\pi r^2\).
Solve Problem
\begin{align*}
\mathcal{E}&=N\frac{\Delta\phi}{\Delta t}\\
&=N\frac{\phi_f-\phi_i}{\Delta t} \\
&=N\frac{B_fA - B_iA}{\Delta t} \\
&=N\frac{A(B_f - B_i)}{\Delta t} \\
(\text{0,30})&=(9)\frac{(\pi r^2)(\text{12} - \text{0,12})}{\text{120}} \\
r^2 &= \frac{(\text{0,30})(\text{120})}{(9)\pi(\text{12} - \text{0,12})} \\
r^2&=\text{0,107175} \\
r&=\text{0,32}\text{ m}
\end{align*}
The solenoid has a radius of \(\text{0,32}\) \(\text{m}\).
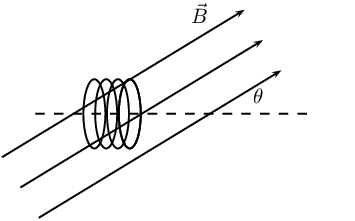
Worked example 3: Faraday's law
Consider a circular coil of 4 turns with radius \(\text{3} \times \text{10}^{-\text{2}}\) \(\text{m}\). The
solenoid is subjected to a varying magnetic field that changes uniformly from \(\text{0,4}\) \(\text{T}\) to
\(\text{3,4}\) \(\text{T}\) in an interval of \(\text{27}\) \(\text{s}\). The axis of the solenoid makes an
angle of \(\text{35}\)\(\text{°}\) to the magnetic field. Find the induced emf.
Identify what is required
We are required to use
Faraday's Law to calculate the induced emf.
Write Faraday's Law
\[\mathcal{E}=-N\frac{\Delta\phi}{\Delta t}\]
We know that the magnetic field is at an angle to the surface normal. This means we must account for the
angle that the field makes with the normal and \(\phi=BA\cos(\theta)\). The starting or initial magnetic
field, \(B_i\), is given as is the final field magnitude, \(B_f\). We want to determine the magnitude of the
emf so we can ignore the minus sign.
The area, \(A\), will be \(\pi r^2\).
Solve Problem
\begin{align*}
\mathcal{E}&=N\frac{\Delta\phi}{\Delta t}\\
&=N\frac{\phi_f-\phi_i}{\Delta t} \\
&=N\frac{B_fA\cos(\theta) - B_iA\cos(\theta)}{\Delta t} \\
&=N\frac{A\cos(\theta)(B_f - B_i)}{\Delta t} \\
&=(4)\frac{(\pi(\text{0,03})^2\cos(\text{35}))(\text{3,4} - \text{0,4})}{\text{27}} \\
&=\text{1,03} \times \text{10}^{-\text{3}}\text{ V}
\end{align*}
The induced current is anti-clockwise as viewed from the direction of the increasing magnetic field.
Real-life applications
The following devices use Faraday's Law in their operation.
-
induction stoves
-
tape players
-
metal detectors
-
transformers
Real-life applications of Faraday's Law
Choose one of the following devices and do some research on the internet, or in a library, how your device
works. You will need to refer to Faraday's Law in your explanation.
-
induction stoves
-
tape players
-
metal detectors
-
transformers
Faraday's Law
Textbook Exercise 10.2
State Faraday's Law of electromagnetic induction in words and write down a mathematical relationship.
The emf, \(\mathcal{E}\), produced around a loop of conductor is proportional to the rate of change
of the magnetic flux, φ, through the area, A, of the loop. This can be stated mathematically as:
\[\mathcal{E} = -N\frac{\Delta\phi}{\Delta t}\]
where \(\phi =B·A\) and B is the strength of the magnetic field. \(N\) is the number of circuit
loops. A magnetic field is measured in units of teslas (T). The minus sign indicates direction and
that the induced emf tends to oppose the change in the magnetic flux. The minus sign can be ignored
when calculating magnitudes.
Describe what happens when a bar magnet is pushed into or pulled out of a solenoid connected to an
ammeter. Draw pictures to support your description.
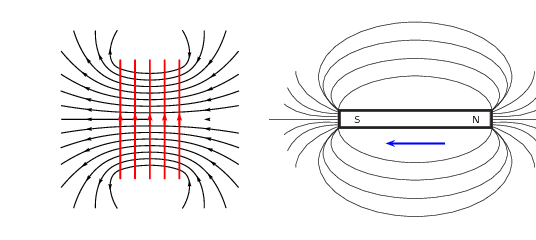
In the case where a north pole is brought towards the solenoid the current will flow so that a north
pole is established at the end of the solenoid closest to the approaching magnet to repel it (verify
using the Right Hand Rule):
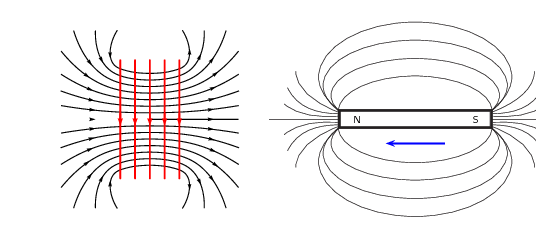
In the case where a north pole is moving away from the solenoid the current will flow so that a south
pole is established at the end of the solenoid closest to the receding magnet to attract it:
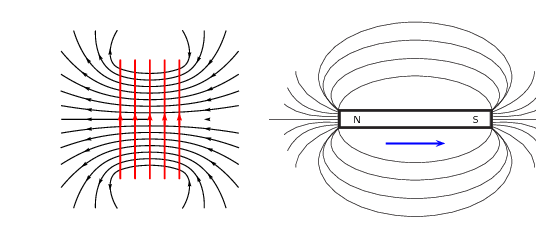
In the case where a south pole is moving away from the solenoid the current will flow so that a north
pole is established at the end of the solenoid closest to the receding magnet to attract it:
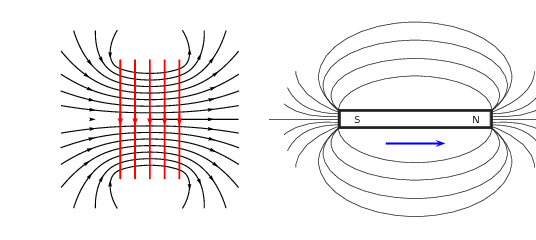
In the case where a south pole is brought towards the solenoid the current will flow so that a south
pole is established at the end of the solenoid closest to the approaching magnet to repel it:
Explain how it is possible for the magnetic flux to be zero when the magnetic field is not zero.
The flux is related to the magnetic field:
\(\phi = BA \cos \theta\)
If \(\cos \theta\) is 0, then the magnetic flux will be 0 even if there is a magnetic field. In this
case the magnetic field is parallel to the surface and does not pass through it.
Use the Right Hand Rule to determine the direction of the induced current in the solenoid below.
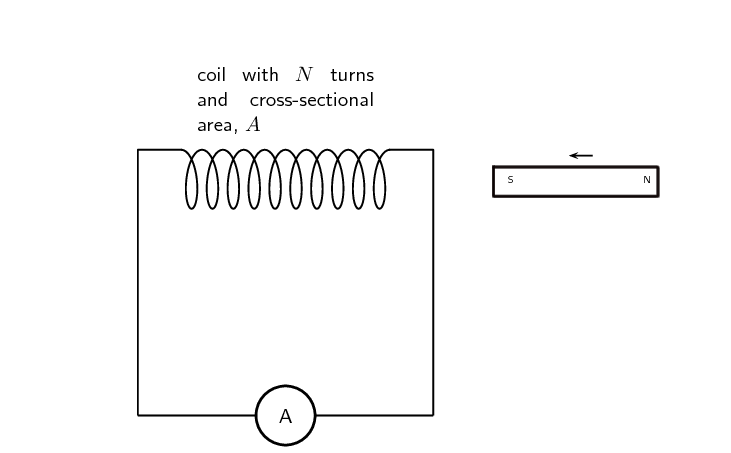
A south pole of a magnet is approaching the solenoid. Lenz's law tells us that the current will flow
so as to oppose the change. A south pole at the end of the solenoid would oppose the approaching south
pole. The current will circulate into the page at the top of the coil so that the thumb on a right
hand points to the left.
Consider a circular coil of 5 turns with radius \(\text{1,73}\) \(\text{m}\). The coil is subjected
to a varying magnetic field that changes uniformly from \(\text{2,18}\) \(\text{T}\) to
\(\text{12,7}\) \(\text{T}\) in an interval of \(\text{3}\) \(\text{minutes}\). The axis of the
solenoid makes an angle of \(\text{27}\)\(\text{°}\) to the magnetic field. Find the induced emf.
We know that the magnetic field is at an angle to the surface normal. This means we must account for
the angle that the field makes with the normal and \(φ = BA \cos(θ)\). The starting or
initial magnetic field, \(B_{i}\), is given as is the final field magnitude, \(B_f\). We want to
determine the magnitude of the emf so we can ignore the minus sign. The area, A, will be
\(πr^{2}\) .
\begin{align*}
\mathcal{E} &= N\frac{\Delta\phi}{\Delta t} \\
& = N\frac{\phi_{f} - \phi_{i}}{\Delta t} \\
& = N\frac{B_{f}A\cos \theta - B_{i}A \cos \theta}{\Delta t} \\
& = N\frac{A\cos \theta(B_{f} - B_{i})}{\Delta t} \\
& = 5 \left( \frac{\pi(\text{1,73})^{2} \cos (\text{27})(\text{12,7} -
\text{2,18})}{\text{3}\times\text{60}} \right) \\
& = \text{2,45}\text{ V}
\end{align*}
\begin{align*}
\mathcal{E} &= N\frac{\Delta\phi}{\Delta t} \\
& = N\frac{\phi_{f} - \phi_{i}}{\Delta t} \\
& = N\frac{B_{f}A\cos \theta - B_{i}A \cos \theta}{\Delta t} \\
& = N\frac{A\cos \theta(B_{f} - B_{i})}{\Delta t} \\
& = 11 \left( \frac{\pi(\text{13,8} \times \text{10}^{-\text{2}})^{2} \cos (\text{13})(\text{2,7}
- \text{5,34})}{12} \right) \\
& = -\text{0,14}\text{ V}
\end{align*}
If the angle is changed to \(\text{67,4}\)\(\text{°}\), what would the radius need to be for
the emf to remain the same?
\begin{align*}
\mathcal{E} &= N\frac{\Delta\phi}{\Delta t} \\
& = N\frac{\phi_{f} - \phi_{i}}{\Delta t} \\
& = N\frac{B_{f}A\cos \theta - B_{i}A \cos \theta}{\Delta t} \\
& = N\frac{A\cos \theta(B_{f} - B_{i})}{\Delta t} \\
-\text{0,14}& = 11 \left( \frac{\pi(r)^{2} \cos (\text{67,4})(\text{2,7} - \text{5,34})}{12}
\right) \\
-\text{1,68}& = -\text{35,06}(r)^{2} \\
r^{2} & = \text{0,0479} \\
r & = \text{0,22}\text{ m}
\end{align*}
Find the change in flux if the emf is \(\text{12}\) \(\text{V}\) over a period of \(\text{12}\)
\(\text{s}\).
\begin{align*}
\mathcal{E} &= N\frac{\Delta\phi}{\Delta t} \\
12 & = 5 \left( \frac{\Delta \phi}{12} \right) \\
\Delta \phi & = \text{28,8}\text{ Wb}
\end{align*}
If the angle is changed to \(\text{45}\)\(\text{°}\), what would the time interval need to
change to for the induced emf to remain the same?
\begin{align*}
\mathcal{E} &= N\frac{\Delta\phi}{\Delta t} \\
& = N\frac{\phi_{f} - \phi_{i}}{\Delta t} \\
& = N\frac{B_{f}A\cos \theta - B_{i}A \cos \theta}{\Delta t} \\
& = \cos\theta \times N\frac{B_{f}A - B_{i}A}{\Delta t}
\end{align*}
All the values remain the same between the two situations described except for the angle and the
time. We can equate the equations for the two scenarios:
\begin{align*}
\mathcal{E}_1 &= \mathcal{E}_2 \\
\cos\theta_1 \times N\frac{B_{f}A - B_{i}A}{\Delta t_1} & = \cos\theta_2 \times N\frac{B_{f}A -
B_{i}A}{\Delta t_2} \\
\cos\theta_1 \frac{1}{\Delta t_1} & = \cos\theta_2 \frac{1}{\Delta t_2} \\
\Delta t_2 & = \frac{\Delta t_1 \cos\theta_2}{\cos \theta_1} \\
\Delta t_2 & = \frac{(\text{12} \cos(\text{45}}{\cos(\text{23})} \\
\Delta t_2 & = \text{9,22}\text{ s}
\end{align*}