The amount of energy per unit charge needed to move that charge between two points in a circuit.
End of chapter exercises
|
Previous
11.4 Chapter summary
|
Next
12.1 Energy changes in chemical reactions
|
Give one word or term for each of the following definitions:
The rate at which electrical energy is converted in an electric circuit.
A law that states that the amount of current through a conductor, at constant temperature, is proportional to the voltage across the resistor.
A \(\text{10}\) \(\text{Ω}\) has a voltage of \(\text{5}\) \(\text{V}\) across it. What is the current through the resistor?
- \(\text{50}\) \(\text{A}\)
- \(\text{5}\) \(\text{A}\)
- \(\text{0,5}\) \(\text{A}\)
- \(\text{7}\) \(\text{A}\)
Three resistors are connected in series. The resistances of the three resistors are: \(\text{10}\) \(\text{Ω}\), \(\text{4}\) \(\text{Ω}\) and \(\text{3}\) \(\text{Ω}\). What is the equivalent series resistance?
- \(\text{1,5}\) \(\text{Ω}\)
- \(\text{17}\) \(\text{Ω}\)
- \(\text{0,68}\) \(\text{Ω}\)
- \(\text{8}\) \(\text{Ω}\)
Three resistors are connected in parallel. The resistances of the three resistors are: \(\text{5}\) \(\text{Ω}\), \(\text{4}\) \(\text{Ω}\) and \(\text{2}\) \(\text{Ω}\). What is the equivalent parallel resistance?
- \(\text{1,05}\) \(\text{Ω}\)
- \(\text{11}\) \(\text{Ω}\)
- \(\text{0,95}\) \(\text{Ω}\)
- \(\text{3}\) \(\text{Ω}\)
A circuit consists of a \(\text{6}\) \(\text{Ω}\) resistor. The voltage across the resistor is \(\text{12}\) \(\text{V}\). How much power is dissipated in the circuit?
- \(\text{864}\) \(\text{W}\)
- \(\text{3}\) \(\text{W}\)
- \(\text{2}\) \(\text{W}\)
- \(\text{24}\) \(\text{W}\)
Calculate the current in the following circuit and then use the current to calculate the voltage drops across each resistor.
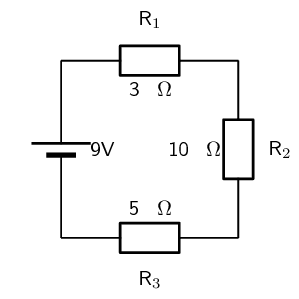
We first calculate the equivalent series resistance:
\begin{align*} R_{s} & = R_{1} + R_{2} + R_{3} \\ & = \text{3} + \text{10} + \text{5} \\ & = \text{18}\text{ Ω} \end{align*}Now we can use Ohm's law to calculate the current:
\begin{align*} I & = \frac{V}{R} \\ & = \frac{\text{9}}{\text{18}} \\ & = \text{0,5}\text{ A} \end{align*}Now we can use the fact that this is a series circuit and that the current is the same everywhere in the circuit to find the voltage drops across each resistor:
\begin{align*} V & = IR \\ & = (\text{0,5})(\text{3}) \\ & = \text{1,5}\text{ V} \end{align*} \begin{align*} V & = IR \\ & = (\text{0,5})(\text{10}) \\ & = \text{5}\text{ V} \end{align*} \begin{align*} V & = IR \\ & = (\text{0,5})(\text{5}) \\ & = \text{2,5}\text{ V} \end{align*}A battery is connected to this arrangement of resistors. The power dissipated in the \(\text{100}\) \(\text{Ω}\) resistor is \(\text{0,81}\) \(\text{W}\). The resistances of voltmeters \(V_{1}\) and \(V_{2}\) are so high that they do not affect the current in the circuit.
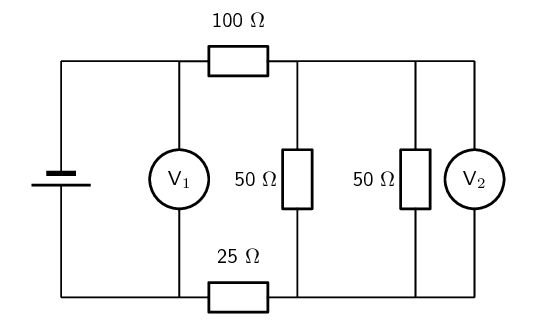
Calculate the current in the \(\text{100}\) \(\text{Ω}\) resistor.
Calculate the reading on voltmeter \(V_{2}\).
This voltmeter is reading the voltage across the one \(\text{50}\) \(\text{Ω}\) resistor so we need to determine what this voltage is.
We know that the current through the parallel combination of resistors is \(\text{0,09}\) \(\text{A}\). We need to calculate the equivalent parallel resistance and then use this with the current to find the voltage across the parallel combination.
\begin{align*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ & = \frac{1}{50} + \frac{1}{50} \\ & = \frac{2}{50} \\ R_{p} & = \text{25}\text{ Ω} \end{align*} \begin{align*} V & = IR \\ & = (\text{0,09})(\text{25}) \\ & = \text{2,25}\text{ V} \end{align*}This is the reading on \(V_{2}\) since the voltage across a parallel combination of resistors is equal to the voltage across each resistor.
Calculate the reading on voltmeter \(V_{1}\).
We need to calculate the equivalent resistance of the circuit first. We already know the equivalent resistance across the parallel combination. So the equivalent resistance is:
\begin{align*} R & = R_{1} + R_{2} + R_{p} \\ & = \text{100} + \text{25} + \text{25} \\ & = \text{150}\text{ Ω} \end{align*}Now we can use Ohm's law to calculate the voltage, since we know the current in the circuit:
\begin{align*} V & = IR \\ & = (\text{0,09})(\text{150}) \\ & = \text{13,5}\text{ V} \end{align*}A kettle is marked \(\text{240}\) \(\text{V}\); \(\text{1 500}\) \(\text{W}\).
Calculate the resistance of the kettle when operating according to the above specifications.
If the kettle takes \(\text{3}\) \(\text{minutes}\) to boil some water, calculate the amount of electrical energy transferred to the kettle.
We first convert the time to seconds:
\[(\text{3})(\text{60}) = \text{180}\text{ s}\]And now we calculate the energy:
\begin{align*} E & = Pt \\ & = (\text{1 500})(\text{180}) \\ & = \text{270 000}\text{ J}\\ & = \text{270}\text{ kJ} \end{align*}Electric Eels
Electric eels have a series of cells from head to tail. When the cells are activated by a nerve impulse, a potential difference is created from head to tail. A healthy electric eel can produce a potential difference of \(\text{600}\) \(\text{V}\).
What is meant by “a potential difference of \(\text{600}\) \(\text{V}\)”?
Potential difference or voltage, \(V\), is the amount of energy per unit charge needed to move that charge between two points in a circuit. In the example of the electric eel this is the amount of energy per unit charge needed to move that charge from the head to the tail.
How much energy is transferred when an electron is moved through a potential difference of \(\text{600}\) \(\text{V}\)?
An electron has a charge of \(-\text{1,69} \times \text{10}^{-\text{19}}\) \(\text{C}\). So we can find the amount of energy needed to move this charge through the potential difference:
\begin{align*} V & = \frac{E}{C} \\ \text{600} & = \frac{E}{-\text{1,69} \times \text{10}^{-\text{19}}} \\ E & = -\text{1,014} \times \text{10}^{-\text{16}}\text{ J} \end{align*}|
Previous
11.4 Chapter summary
|
Table of Contents |
Next
12.1 Energy changes in chemical reactions
|
