20.2 Graphical representation of vectors | Vectors and scalars

20.1 Introduction to vectors and scalars

20.2 Graphical representation of vectors (ESAGK)

Vectors are drawn as arrows. An arrow has both a magnitude (how long it is) and a direction (the direction in which it points). The starting point of a vector is known as the tail and the end point is known as the head.

Directions (ESAGL)

There are many acceptable methods of writing vectors. As long as the vector has a magnitude and a direction, it is most likely acceptable. These different methods come from the different methods of representing a direction for a vector.

Relative directions

The simplest way to show direction is with relative directions: to the left, to the right, forward, backward, up and down.

Compass directions

Another common method of expressing directions is to use the points of a compass: North, South, East, and West. If a vector does not point exactly in one of the compass directions, then we use an angle. For example, we can have a vector pointing $\text{40}$$\text{°}$ North of West. Start with the vector pointing along the West direction (look at the dashed arrow below), then rotate the vector towards the north until there is a $\text{40}$$\text{°}$ angle between the vector and the West direction (the solid arrow below). The direction of this vector can also be described as: W $\text{40}$$\text{°}$ N (West $\text{40}$$\text{°}$ North); or N $\text{50}$$\text{°}$ W (North $\text{50}$$\text{°}$ West).

Bearing

A further method of expressing direction is to use a bearing. A bearing is a direction relative to a fixed point. Given just an angle, the convention is to define the angle clockwise with respect to North. So, a vector with a direction of $\text{110}$$\text{°}$ has been rotated clockwise $\text{110}$$\text{°}$ relative to North. A bearing is always written as a three digit number, for example $\text{275}$$\text{°}$ or $\text{080}$$\text{°}$ (for $\text{80}$$\text{°}$).

Scalars and vectors

Textbook Exercise 20.2

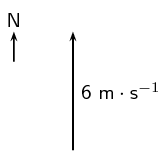
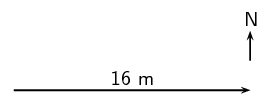
Classify the following quantities as scalars or vectors:

$\text{12}$ $\text{km}$
$\text{1}$ $\text{m}$ south
$\text{2}$ $\text{m·s$^{-1}$}$, $\text{45}$$\text{°}$
$\text{075}$$\text{°}$, $\text{2}$ $\text{cm}$
$\text{100}$ $\text{km·h$^{-1}$}$, $\text{0}$$\text{°}$

Solution not yet available

Use two different notations to write down the direction of the vector in each of the following diagrams:

Solution not yet available

Drawing vectors (ESAGM)

In order to draw a vector accurately we must represent its magnitude properly and include a reference direction in the diagram. A scale allows us to translate the length of the arrow into the vector's magnitude. For instance if one chooses a scale of $\text{1}$ $\text{cm}$ = $\text{2}$ $\text{N}$ ($\text{1}$ $\text{cm}$ represents $\text{2}$ $\text{N}$), a force of $\text{20}$ $\text{N}$ towards the East would be represented as an arrow $\text{10}$ $\text{cm}$ long pointing towards the right. The points of a compass are often used to show direction or alternatively an arrow pointing in the reference direction.