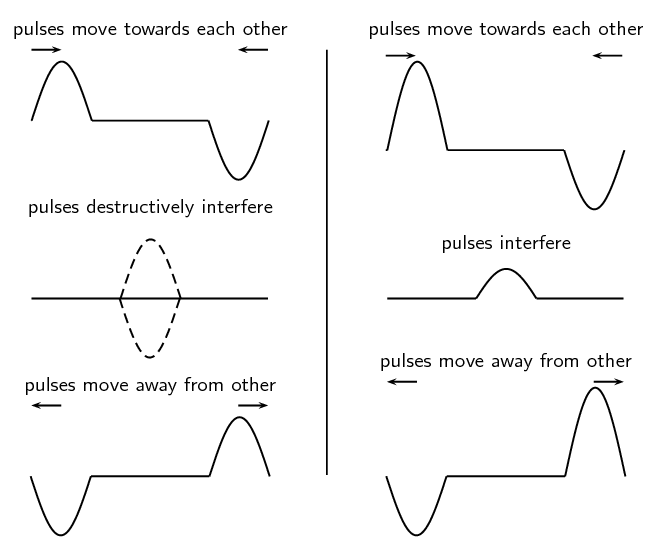
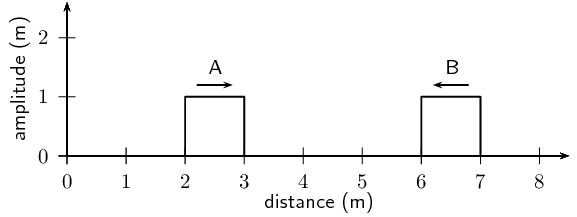
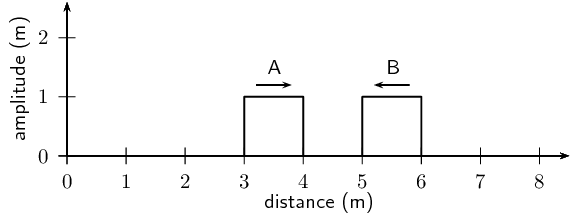
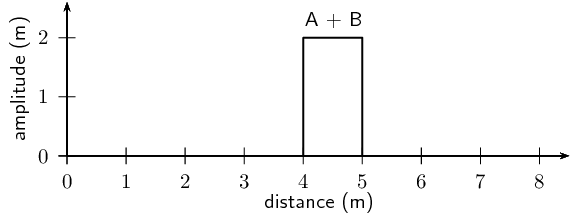
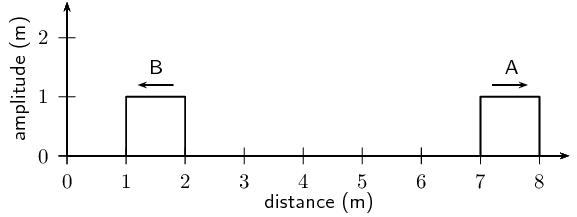
For the following pulse, draw the resulting wave forms after \(\text{1}\)
\(\text{s}\), \(\text{2}\) \(\text{s}\), \(\text{3}\) \(\text{s}\),
\(\text{4}\) \(\text{s}\) and \(\text{5}\) \(\text{s}\). Each pulse is
travelling at \(\text{1}\) \(\text{m·s$^{-1}$}\). Each block represents
\(\text{1}\) \(\text{m}\). The pulses are shown as thick black lines and the
undisplaced medium as dashed lines.
Solution not yet available
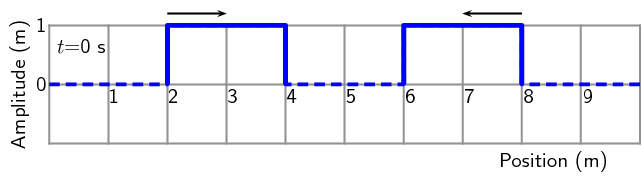
For the following pulse, draw the resulting wave forms after \(\text{1}\)
\(\text{s}\), \(\text{2}\) \(\text{s}\), \(\text{3}\) \(\text{s}\),
\(\text{4}\) \(\text{s}\) and \(\text{5}\) \(\text{s}\). Each pulse is
travelling at \(\text{1}\) \(\text{m·s$^{-1}$}\). Each block represents
\(\text{1}\) \(\text{m}\). The pulses are shown as thick black lines and the
undisplaced medium as dashed lines.
Solution not yet available
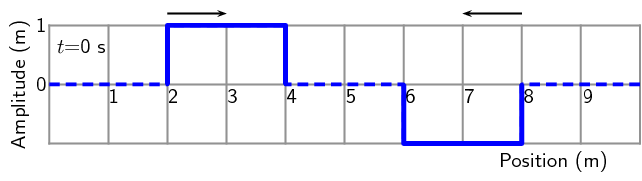
For the following pulse, draw the resulting wave forms after \(\text{1}\)
\(\text{s}\), \(\text{2}\) \(\text{s}\), \(\text{3}\) \(\text{s}\),
\(\text{4}\) \(\text{s}\) and \(\text{5}\) \(\text{s}\). Each pulse is
travelling at \(\text{1}\) \(\text{m·s$^{-1}$}\). Each block represents
\(\text{1}\) \(\text{m}\). The pulses are shown as thick black lines and the
undisplaced medium as dashed lines.
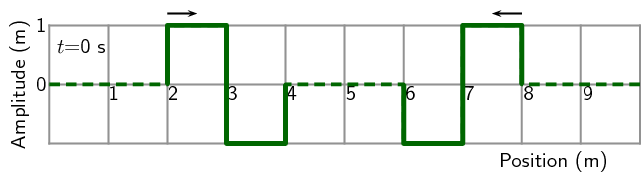
Solution not yet available
For the following pulse, draw the resulting wave forms after \(\text{1}\)
\(\text{s}\), \(\text{2}\) \(\text{s}\), \(\text{3}\) \(\text{s}\),
\(\text{4}\) \(\text{s}\) and \(\text{5}\) \(\text{s}\). Each pulse is
travelling at \(\text{1}\) \(\text{m·s$^{-1}$}\). Each block represents
\(\text{1}\) \(\text{m}\). The pulses are shown as thick black lines and the
undisplaced medium as dashed lines.
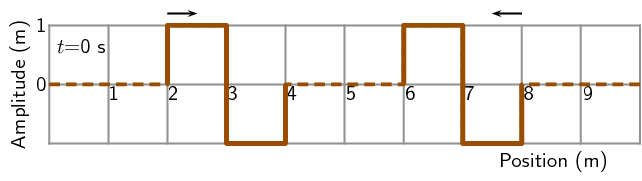
Solution not yet available
For the following pulse, draw the resulting wave forms after \(\text{1}\)
\(\text{s}\), \(\text{2}\) \(\text{s}\), \(\text{3}\) \(\text{s}\),
\(\text{4}\) \(\text{s}\) and \(\text{5}\) \(\text{s}\). Each pulse is
travelling at \(\text{1}\) \(\text{m·s$^{-1}$}\). Each block represents
\(\text{1}\) \(\text{m}\). The pulses are shown as thick black lines and the
undisplaced medium as dashed lines.
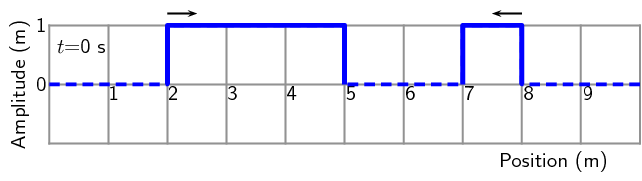
Solution not yet available
For the following pulse, draw the resulting wave forms after \(\text{1}\)
\(\text{s}\), \(\text{2}\) \(\text{s}\), \(\text{3}\) \(\text{s}\),
\(\text{4}\) \(\text{s}\) and \(\text{5}\) \(\text{s}\). Each pulse is
travelling at \(\text{1}\) \(\text{m·s$^{-1}$}\). Each block represents
\(\text{1}\) \(\text{m}\). The pulses are shown as thick black lines and the
undisplaced medium as dashed lines.
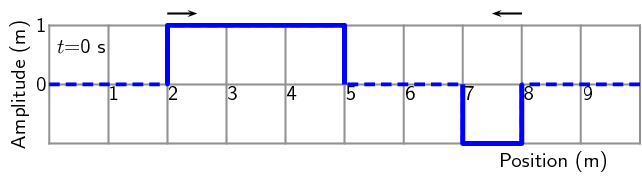
Solution not yet available
What is superposition of waves?
Solution not yet available
What is constructive interference?
Solution not yet available
What is destructive interference?
Solution not yet available