1.7 Working with money: Budgets, savings, discount, interest and exchange rates
In business and in everyday life, we use money to pay for services and goods. There are different financial models, and it is useful to understand how the prices are set. It is also important to save money and budget for different expenses.
Budgets and savings
A budget is a plan about how you will spend, and save, your money. Budgets are a very important part of planning for a sound financial future.
You can include saving money in your budget. Think of what you want to save money for and work out how long it will take you. For example, if your goal is to save \(\text{R} 200\) in \(10\) months, you would need to save \(\text{R} 20\) every month. You could also keep track of different amounts you save to make sure you still have \(\text{R} 200\) at the end of the \(10^{\text{th}}\) month.
Worked Example 1.28: Calculating budgets and savings
Anita gets \(\text{R} 250\) pocket money per month. She budgets to spend the following each month:
- \(\text{R} 50\) on snacks
- \(\text{R} 30\) on airtime
- \(\text{R} 25\) on transport
She saves the rest.
How much will Anita save each month, if she keeps to her budget?
Calculate how much Anita has budgeted to spend
Anita plans to spend:
- \(\text{R} 50\) on snacks
- \(\text{R} 30\) on airtime
- \(\text{R} 25\) on transport
Therefore, Anita plans to spend \(\text{R} 105\) each month.
Calculate how much money is left over
Anita gets \(\text{R} 250\) each month.
\[250 - 105 = 145\]Therefore, Anita saves \(\text{R} 145\) each month.
There are \(12\) months in a year.
If Anita saves \(\text{R} 145\) per month for a year, then:
\[145 \times 12 = 1\ 740\]Anita will save \(\text{R} 1\ 740\) in a year.
Profit and loss
When people start a business, they need to be able to work with cash flows and monitor their sales. There are different costs involved to make the sales. These costs are needed to perform business. For example, to make clothes you need to buy fabric, a sewing machine, needles, and threads. These are costs, and when you want to sell clothes you made, you will factor these costs in so you can make a profit.
- profit
- the amount by which the selling price exceeds the costs: profit = selling price – cost price
When the money you get exceeds the expenses or the initial costs, then you make a profit. If you make less money then you spend, then you make a loss.
- loss
- an amount by which the costs exceed the selling price: loss = cost price – selling price
Worked example 1.29: Calculating profit and loss
Phillip buys a bulk bag of \(130\) packets of sweets for \(\text{R} 236\). He sells them for \(\text{R} 2\) each.
If he sells all of the items:
- Will he make a profit or a loss?
- How much of a profit or loss will he make?
Calculate how much money Phillip will get for selling all of the packets of sweets.
Phillip sells \(130\) packets of sweets for \(\text{R} 2\) each.
\[130 \times 2 = 260\]Therefore, Phillip gets \(\text{R} 260\) for selling the packets of sweets.
Phillip earns \(\text{R} 260\) income in the business of selling packets of sweets.
Compare Phillip’s income to his expenses.
Phillip bought the packets of sweets for \(\text{R} 236\).
Phillip’s expenses were \(\text{R} 236\).
- Income \(\text{R} 260\)
- Expenses \(\text{R} 236\)
The amount that Phillip earned from selling the packets of sweets is greater than the amount that he spent to buy them. Phillip’s income was greater than his expenses.
Therefore, Phillip made a profit.
Calculate the profit.
The difference between Phillip’s income and expenses is:
\[\text{R} 260 - \text{R} 236 = \text{R} 24\]Therefore, Phillip made a \(\text{R} 24\) profit from selling the packets of sweets.
Discount
The amount for which a dealer buys an article from a producer or manufacturer is called the cost price. The price marked on the article is called the marked price and the price of the article after mark-up and/or a discount is the selling price.
- cost price
- the amount for which someone buys something from a producer
- discount
- an amount that is subtracted from the marked price to determine the selling price
- selling price
- the amount for which a buyer buys a product; this amount includes the seller’s mark-up and may also include a discount
For example, we can look at this scenario and try to understand the problem.
Rashid is a furniture dealer. He buys a couch for \(\text{R} 2\ 420\). He displays the couch in his showroom with the price marked as \(\text{R} 3\ 200\). Rashid offers a discount of \(\text{R} 320\) to customers who pay cash.
- The cost price of the couch in Rashid’s furniture shop is \(\text{R} 2\ 420\). This is the amount he paid for it.
- The marked price of the couch is \(\text{R} 3\ 200\). This is the amount that is displayed on the couch in his showroom.
- The selling price for a customer who pays cash is \(\text{R} 3\ 200 − \text{R} 320 = \text{R} 2\ 880\). The cash payment attracts a discount of \(\text{R} 320\), meaning that the customer will pay less.
The discount on an article is always less than the marked price of the article. In fact, it is only a fraction of the marked price. The discount of \(\text{R} 320\) that Rashid offers on the couch is \(10\) hundredths of the marked price.
Another word for hundredths is percentage, and the symbol for percentage is \(\%\). So, we can say that Rashid offers a discount of \(10\%\).
For example, \(18\%\) is \(18\) hundredths, and \(25\%\) is \(25\) hundredths.
- percentage
- a value of hundredths
\(\%\) is a symbol for hundredths. \(8\%\) means \(8\) hundredths and \(15%\) means \(15\) hundredths.
The symbol \(\%\) is just another way of writing the common fraction notation for hundredths.
\(8\%\) is \(\frac{8}{100}\).
A discount of \(6\%\) on an article can be calculated in two steps:
- Calculate \(1\) hundredth of the marked price (divide by \(100\)).
- Calculate \(6\) hundredths of the marked price (multiply by \(6\)).
Worked Example 1.30: Calculating discounts
Calculate the amount of the discount on the marked price of a jacket:
\(6\%\) on \(\text{R} 3\ 600\)
Calculate \(1\) hundredth of the amount (divide by \(100\)).
\[3\ 600 \div 100 = 36\]Calculate \(6\) hundredths of the marked price (multiply by \(6\)).
\[36 \times 6 = 216\]The discount amount is \(\text{R} 216\).
Worked Example 1.31: Calculating discounts
Calculate the amount of the discount on the marked price of a laptop:
\(8\%\) on \(\text{R} 9\ 350\)
Calculate \(1\) hundredth of the marked price (divide by \(100\)).
\[9\ 350 \div 100 = \text{93,5}\]Calculate \(8\) hundredths of the marked price (multiply by \(8\)).
\[\text{93,5} \times 8 = 748\]The discount amount is \(\text{R} 748\).
Interest
When a person borrows money from a bank or some other institution, they normally have to pay for the use of the money. This is called interest. The bank charges the interest on the borrowed amount.
- interest
- the amount that is paid at a given rate for the use of money that is lent
For example, let’s look at this scenario and try to understand the problem.
Lebo borrows \(\text{R} 7\ 000\) from a bank at \(14\%\) interest for one year. How much does she have to pay back to the bank at the end of the period?
- The amount borrowed is \(\text{R} 7\ 000\).
- The bank charges \(14\%\) interest.
One way to solve this problem is to:
- calculate the \(\%\) interest
- add the interest to the original amount to find the total.
So, \(7\ 000 \div 100 = 70\) and \(70 \times 14 = 980\). The amount of interest is \(\text{R} 980\).
Now, add the interest to the amount borrowed. \(7\ 000 + 980 = 7\ 980\).
The total that Lebo needs to pay back to the bank is \(\text{R} 7\ 980\).
Worked Example 1.32: Calculating interest
Jabu invests \(\text{R} 5\ 600\) for one year at \(8\%\) interest.
- What will the value of his investment be at the end of that year?
- At the end of the year Jabu does not withdraw the investment or the interest earned, but reinvests it for another year. How much will it be worth at the end of the second year?
Calculate the \(\%\) interest.
To answer the first question, we need to calculate \(8\%\) of \(\text{R} 5\ 600\) and add it to \(\text{R} 5\ 600\).
\[\begin{align} 5\ 600 \div 100 &= 56 \\ 56 \times 8 &= 448 \end{align}\]So, the amount of interest is \(\text{R} 448\).
Add the interest to the original amount to find the total.
\[5\ 600 + 448 = 6\ 048\]The total value at the end of the year is \(\text{R} 6\ 048\).
Calculate the \(\%\) interest.
Jabu keeps earning the \(8\%\) interest, but he now starts with the new amount = \(\text{R} 6\ 048\).
\[\begin{align} \text{6 048} \div 100 &= \text{60,48} \\ \text{60,48} \times 8 &= \text{483,84} \end{align}\]So, the amount of interest is \(\text{R}\,\text{483,84}\).
Add the interest to the amount at the end of the first year to find the total.
\[6\ 048 + \text{483,84} = \text{6 531,84}\]The total value at the end of the second year is \(\text{R}\,\text{6 531,84}\).
VAT calculations
Value added tax (VAT) is an amount added to the price of goods. VAT goes to the government to spend on services for the citizens of the country. In South Africa, when you see a price in the shops, VAT has usually already been added.
The price including VAT is calculated by adding \(15\%\) to the original price (excluding VAT). Adding \(15\%\) VAT means that we have to pay \(100\% + 15\% = 115\%\) of the original price. This is the same as multiplying by \(115\%\).
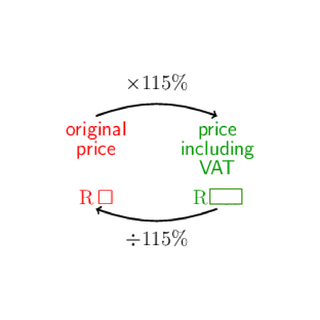
When you only know the price including VAT, you need to work backwards. To work backwards from the price including VAT to the original price, we must do the inverse operation. Instead of multiplying by \(115\%\), we must divide by \(115\%\).
Working with percentages, keep in mind that \(\%\) is ‘out of \(100\)’, so remember to divide by \(100\):
\[115\% = \frac{115}{100} = \text{1,15}\]Worked Example 1.33: Calculations with VAT
Jaya makes beaded bracelets to sell in her shop. The price excluding VAT of a bracelet is \(\text{R}\,60\). What is the price including \(15\%\) VAT?
Decide on the operation you need.
The price including VAT is calculated by adding \(15\%\) to the original price (excluding VAT). Jaya has to make the marked price \(100\% + 15\% = 115\%\) of the cost price. This is the same as multiplying by \(115\%\).
Calculate the price including VAT.
\[\begin{align} 115\% &= \frac{115}{100} \\ &= \text{1,15} \end{align}\] \[\begin{align} 160 \times 115\% &= 160 \times \text{1,15} \\ &= 184 \end{align}\]Therefore, the price including VAT is \(\text{R}\,\text{184}\).
Worked Example 1.34: Calculations with VAT
Molebatsi makes beaded necklaces to sell in his shop. The price of one of his beaded necklaces is \(\text{R}\,207\), including \(15\%\) VAT. What is the original price of the necklace, excluding VAT?

Decide on the operation.
We only know the price including VAT. To work backwards from the price including VAT to the original price, we must do the inverse operation. Instead of multiplying by \(115\%\), we must divide by \(115\%\).
Calculate the price excluding VAT.
\[\begin{align} 115\% &= \frac{115}{100} \\ &= \text{1,15} \end{align}\] \[\begin{align} 207 \div 115\% &= 207 \div \text{1,15} \\ &= 180 \end{align}\]The original price of the necklace is \(\text{R 180}\) (excluding VAT).
This is how much money Molebatsi earns for selling the necklace. He has to pay the remaining \(\text{R} 207 – \text{R}\,180 = \text{R}\,27\) to the government as tax.
Hire purchase
A hire purchase agreement is a credit agreement between a buyer and a financial institution. If the buyer does not have enough money upfront to buy something (for example, a laptop or a fridge), they can choose to make use of a hire purchase agreement instead. They then pay an agreed amount in monthly payments. The item does not belong to them until the final payment is made.
To calculate the amount owed on a hire purchase agreement:
- Calculate the balance owed on the cash price: balance = cash price − deposit.
- Calculate the total interest on the balance owed, using simple interest.
- Total amount owed = balance + total interest.
Hire purchase agreements always use simple interest to calculate monthly repayments. Simple interest means that interest is calculated on the original amount in each year. So, the amount of interest charged is the same in each year.
Worked Example 1.35: Calculating hire purchase repayments

The cash price of a bedroom suite is \(\text{R}\,4\ 500\). Ayanda buys the bedroom suite on a hire purchase agreement instead of paying cash. There is a special deal and no deposit is required. Ayanda pays for the bedroom suite in equal monthly instalments over \(3\) years. Interest is \(40\%\) per year.
- How much does Ayanda pay in total over the \(3\) years?
- How much does Ayanda pay per month over the \(3\) years?
Calculate the yearly interest.
Ayanda does not have to pay a deposit. She is charged \(40\%\) simple interest per year on \(\text{R}\,\text{4 500}\).
\[\begin{align} 40\% \text{ of } 4\ 500 &= \frac{40}{100} \times 4\ 500 \\ &= 1\ 800 \end{align}\]Therefore, she pays \(\text{R}\,1\ 800\) interest each year for \(3\) years.
Calculate the total interest.
\[1\ 800 \times 3 = 5\ 400\]Therefore, Ayanda must pay \(\text{R}\,5\ 400\) in interest in total.
Add the total interest to the balance owing.
\[4\ 500 + 5\ 400 = 9\ 900\]Therefore, Ayanda must pay \(\text{R}\,9\ 900\) over \(3\) years.
This is more than double the cash price! If Ayanda had saved up for the bedroom suite instead of buying it on hire purchase, she could have saved herself a lot of money.
Divide the total amount by the number of months.
In Step 3. we worked out that Ayanda must pay \(\text{R}\,9\ 900\) for the bedroom suite. She repays this amount in equal monthly instalments over \(3\) years. There are \(36\) months in \(3\) years, since \(12 \times 3 = 36\).
\[9\ 900 \div 36 = 275\]Therefore, Ayanda pays \(\text{R}\,275\) per month.
Exchange rates
Different countries use different currencies, which is another name for money. Currency is something that we use to exchange for food, clothes, and services. When you travel to another country or read news about that country, you will often need to understand the relationship between the country’s currency and the South African rand. This is called the exchange rate.
- exchange rate
- the amount of rand that we pay to get another currency.
In South Africa, we use the rand (\(\text{R}\)). In Botswana, for example, they use the pula (\(\text{P}\)). If you go to Botswana and want to buy something there, you have to exchange rand for pula.
Worked Example 1.36: Working with exchange rates
Andani is on holiday in Botswana. The currency in Botswana is the pula (\(\text{P}\)). Andani buys a meal at KFC for \(\text{P} 96\).
The exchange rate between the South African rand and the Botswanan pula (\(\text{P}\)) is \(\text{R}\,1 = \text{P}\,3\). Determine the price of Andani’s meal in rand.
Use the exchange rate of \(\text{R} 1 = \text{P} 3\).
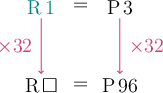
Divide the amount by the exchange rate.
You can answer this question by dividing the pula amount by the exchange rate:
\[96 \div 3 = 32\]The rand price of Andani’s meal is \(\text{R} 32\).
