17.6 Converting between different units
Surface area is measured in square units. Surface area can be expressed in square millimetres
(\(\text{mm}^2\)), square centimetres (\(\text{cm}^2\)), square metres (\(\text{m}^2\)) and also square
kilometres (\(\text{km}^2\)).
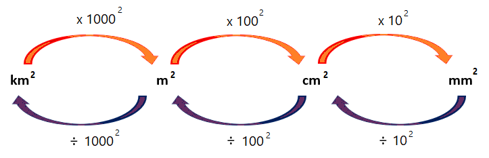
The diagram below shows how to convert between the different units of area.
Worked Example 17.10: Converting between units of
area
Convert \(157 \text{ mm}^2\) to square centimetres.
Divide the area by \(100\).
To convert from square millimetres to square centimetres, we divide the area by \(100\):
\[\begin{align}
157 \text{ mm}^2 &= 157 \div 100 \\
&= \text{1,57} \text{ cm}^2
\end{align}\]
Worked Example 17.11: Converting between units of
area
Convert \(\text{3,08} \text{ m}^2\) to square centimetres.
Multiply the area by \(100^{2}\).
To convert from square metres to square centimetres, we multiply the area by \(100^2\):
\[\begin{align}
\text{3,08} \text{ m}^2 &= \text{3,08} \times \text{10 000} \\
&= \text{30 800} \text{ cm}^2
\end{align}\]
Exercise 17.1
Convert each area to square centimetres.
-
\(\text{2,06} \text{ m}^2\)
-
\(\text{7 423} \text{ mm}^2\)
-
\(\text{0,015} \text{ m}^2\)
-
\(\text{842,5} \text{ mm}^2\)
-
\(\text{0,416} \text{ m}^2\)
-
\(\text{20 600} \text{ cm}^2\)
-
\(\text{74,23} \text{ cm}^2\)
-
\(\text{150} \text{ cm}^2\)
-
\(\text{8,425} \text{ cm}^2\)
-
\(\text{4 160} \text{ cm}^2\)
Convert each area to square millimetres.
-
\(\text{3,4} \text{ cm}^2\)
-
\(\text{0,009} \text{ m}^2\)
-
\(\text{0,62} \text{ cm}^2\)
-
\(\text{0,00045} \text{ m}^2\)
-
\(\text{72,6} \text{ cm}^2\)
-
\(\text{340} \text{ mm}^2\)
-
\(\text{9 000} \text{ mm}^2\)
-
\(\text{62} \text{ mm}^2\)
-
\(\text{4 500} \text{ mm}^2\)
-
\(\text{7 260} \text{ mm}^2\)
Convert each area to square metres.
-
\(\text{1 753} \text{ cm}^2\)
-
\(\text{85 000} \text{ mm}^2\)
-
\(\text{55 010} \text{ cm}^2\)
-
\(\text{2,04} \text{ km}^2\)
-
\(\text{360} \text{ cm}^2\)
-
\(\text{0,1753} \text{ m}^2\)
-
\(\text{0,085} \text{ m}^2\)
-
\(\text{5,501} \text{ m}^2\)
-
\(\text{2 040 000} \text{ m}^2\)
-
\(\text{0,036} \text{ m}^2\)
Volume is measured in cubic units. The volume of an object can be expressed in cubic millimetres
(\(\text{mm}^3\)), cubic centimetres (\(\text{cm}^3\)), cubic metres (\(\text{m}^3\)) and also cubic kilometres
(\(\text{km}^3\)).
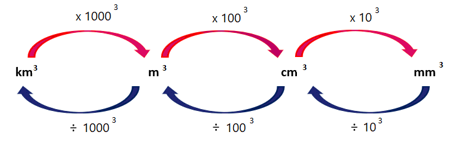
The diagram below shows how to convert between the different units of volume.
Worked Example 17.12: Converting between units
of volume
Convert \(\text{8 259} \text{ mm}^3\) to cubic centimetres.
Divide the volume by \(10^{3}\).
To convert from cubic millimetres to cubic centimetres, we divide the volume by \(10^3 = 1\ 000\):
\[\begin{align}
\text{8 259} \text{ mm}^3 &= \text{8 259} \div \text{1 000} \\
&= \text{8,259} \text{ cm}^3
\end{align}\]
Worked Example 17.13: Converting between units
of volume
Convert \(\text{3,08} \text{ m}^3\) to cubic centimetres.
Multiply the volume by \(100^{3}\).
To convert from cubic metres to cubic centimetres, we multiply the volume by \(100^3 = 1\ 000\ 000\):
\[\begin{align}
\text{3,08} \text{ m}^3 &= \text{3,08} \times \text{1 000 000} \\
&= \text{3 080 000} \text{ cm}^3
\end{align}\]
Capacity can be expressed in millilitres (\(\text{ml}\)), litres (\(\text{l)}\) and kilolitres (\(\text{kl}\)).
Capacity can also be measured in cubic centimetres (\(\text{cm}^3\)) and cubic metres (\(\text{m}^3\)).
-
\(1 \text{ cm}^3 = 1 \text{ ml}\)
-
\(1\ 000 \text{ cm}^3 = 1 \text{ litre}\)
Worked Example 17.14: Converting
between units of volume and capacity
Convert \(560 \text{ cm}^3\) to litres.
Divide the volume by \(1\ 000\).
To convert from cubic centimetres to litres, we divide the volume by \(1\ 000\):
\[1 \text{ cm}^3 = 1 \text{ ml}\]
So \(560 \text{ cm}^3 = 560 \text{ ml}\).
And we know that \(\text{1 000} \text{ ml} = 1 \text{ litre}\).
Therefore,
\[\begin{align}
\text{560} \text{ cm}^3 &= \text{560} \div \text{1 000} \\
&= \text{0,56} \text{ litres}
\end{align}\]