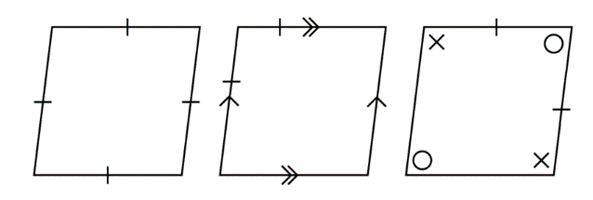
Identify each shape.
- Trapezium
- Trapezium
- Kite
- Trapezium
- Kite
|
Previous
Classifying triangles
|
Next
Similar and congruent shapes
|
A quadrilateral is a four-sided polygon. A quadrilateral has four straight sides and four vertices. Different quadrilaterals have different angle and side relationships. The figure below shows five different types of quadrilaterals:

A quadrilateral can be divided into two triangles by drawing a diagonal from one vertex to the opposite vertex. As a result, we can deduce that the sum of the interior angles of a quadrilateral is equal to twice the sum of the interior angles of a triangle:
\[\text{Sum of angles of quadrilateral} = 2 \times 180^{\circ} = 360^{\circ}\]A parallelogram is a quadrilateral with both pairs of opposite sides equal and parallel.
The diagram shows parallelogram \(ABCD\):
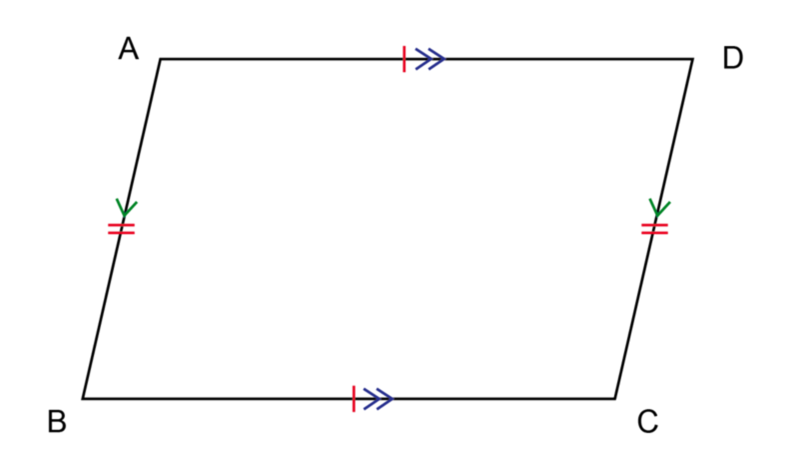
A parallelogram has four interior angles. A special property of the interior angles of parallelogram is that the interior opposite angles are equal. A parallelogram has two pairs of opposite angles that are equal.
The diagram shows parallelogram \(PQRS\) with opposite angles equal: \(\hat{P} = \hat{R}\) and \(\hat{Q} = \hat{S}\).

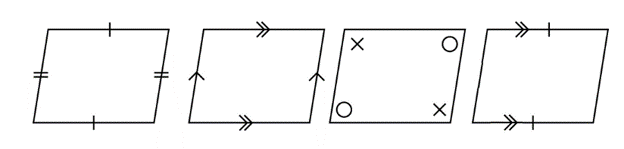
A quadrilateral can be classified as a parallelogram if any of the following properties are true:
\(QRST\) is a parallelogram with \(\hat{Q} = 54^{\circ}\), \(\hat{R} = 126^{\circ}\), \(QT = 9 \text{ units}\), \(RS = 9 \text{ units}\) and \(TS = 5 \text{ units}\). Find the values of \(w\), \(x\) and \(y\).
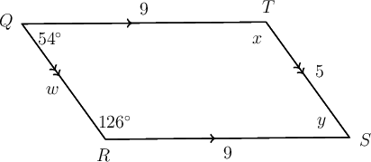
In parallelogram \(QRST\):
\[\begin{align} \hat{Q} &= \hat{S}\ (\text{opp. } \angle\text{s equal}) \\ \hat{Q} &= y \\ &= 54^{\circ} \end{align}\] \[\begin{align} \hat{R} &= \hat{T}\ (\text{opp. } \angle\text{s equal}) \\ \hat{R} &= x \\ &= 126^{\circ} \end{align}\] \[\begin{align} QR &= TS\ (\text{opp. sides equal}) \\ QR &= w \\ &= 5 \text{ units} \end{align}\]In parallelogram \(QRST\), \(y = 54^{\circ}\), \(x = 126^{\circ}\) and \(w = 5 \text{ units}\).
A rectangle is quadrilateral with opposites equal and parallel and interior angles equal to \(90^{\circ}\).
The diagonal of a rectangle divides the rectangle into two right-angled triangles. We can use the theorem of Pythagoras to calculate the length of unknown sides of these triangles. You will learn more about this theorem in Chapter 15.
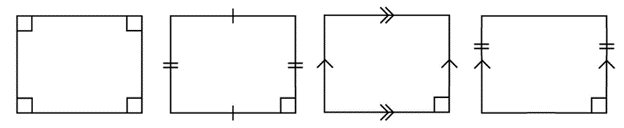
A quadrilateral can be classified as a rectangle if any of the following properties are true:
\(MNPQ\) is a rectangle with \(\hat{N} = 90^{\circ}\) and \(M\hat{P}N = 59^{\circ}\).
Find the values of \(a\), \(b\), \(c\) and \(d\).
In rectangle \(MNPQ\):
\[\begin{align} \hat{Q} &= \hat{N} = 90^{\circ}\ (\text{opp. } \angle\text{s equal}) \\ \hat{Q} &= a = 90^{\circ} \end{align}\]In rectangle \(MNPQ\):
\[\begin{align} \hat{M} &= \hat{P} = 90^{\circ}\ (\text{opp. } \angle\text{s equal}) \\ b + 59^{\circ} &= 90^{\circ}\ (\text{right angle of rectangle}) \\ b &= 90^{\circ} − 59^{\circ} \\ b &= 31^{\circ} \end{align}\]In \(\triangle MNP\):
\[\begin{align} d + 90^{\circ} + 59^{\circ} &= 180^{\circ} (\angle \text{ sum of } \triangle) \\ d &= 180^{\circ} − 149^{\circ} \\ d &= 31^{\circ} \end{align}\]In rectangle \(MNPQ\):
\[\begin{align} c + d &= 90^{\circ}\ (\text{opp. } \angle\text{s equal}) \\ c &= 90^{\circ} − 31^{\circ} \\ c &= 59^{\circ} \end{align}\]In rectangle \(MNPQ\), \(a = 90^{\circ}\), \(b = 31^{\circ}\), \(c = 59^{\circ}\) and \(d = 31^{\circ}\).
A square is parallelogram with all sides equal and interior angles equal to \(90^{\circ}\).
A diagonal divides the square into two right-angled isosceles triangles. We can use the theorem of Pythagoras to calculate the length of unknown sides of these triangles.
A quadrilateral can be classified as a square if any of the following properties are true:
\(ABCD\) is a square with \(\hat{D} = 3t\), \(AB = s\) and \(AD = 7 \text{ cm}\).
Find the values of \(s\) and \(t\).
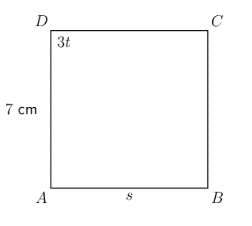
In square \(ABCD\):
\[\begin{align} \hat{D} &= 3t = 90^{\circ}\ (\text{right angle of square}) \\ 3t &= 90^{\circ} \\ \frac{3t}{3} &= \frac{90^{\circ}}{3} \\ t &= 30^{\circ} \end{align}\]In square \(ABCD\):
\[\begin{align} AD &= AB = s\ (\text{equal sides of square}) \\ AD &= 7 \text{ cm} \\ \therefore AB &= s = 7 \text{ cm} \end{align}\]In square \(ABCD\), \(t = 30^{\circ}\) and \(s = 7 \text{ cm}\)
A rhombus is a quadrilateral with both pairs of opposite sides parallel and all sides equal.
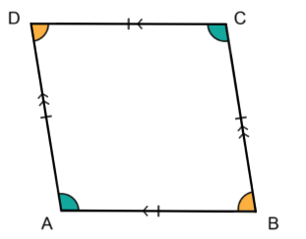
A rhombus has two pairs of opposite angles that are equal. A diagonal divides the rhombus into two isosceles triangles.
A quadrilateral can be classified as a rhombus if any of the following properties are true:
\(EFGH\) is a rhombus with \(\hat{H} = x + 40^{\circ}\), \(\hat{F} = 102^{\circ}\), \(FE= w\) and \(FG = 10 \text{ m}\). Find the values of \(x\) and \(w\).
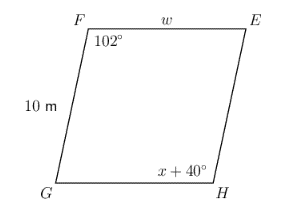
In rhombus \(EFGH\):
\[\begin{align} \hat{F} &= \hat{H} = 102^{\circ}\ (\text{opp. } \angle\text{s equal}) \\ \hat{H} &= x + 40^{\circ} = 102^{\circ} \\ x &= 102^{\circ} − 40^{\circ} \\ \therefore x &= 62^{\circ} \end{align}\]In rhombus \(EFGH\):
\[\begin{align} FG &= FE = w\ (\text{equal sides of rhombus}) \\ FG &= 10 \text{ m} \\ \therefore w &= 10 \text{ m} \end{align}\]In rhombus \(EFGH\), \(x = 62^{\circ}\) and \(w = 10 \text{ m}\)
A trapezium is a quadrilateral with one pair of opposite sides parallel.
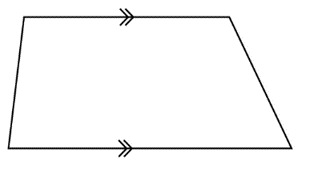
An isosceles trapezium has one pair of opposite sides parallel and the other pair of opposite sides equal. The base angles of an isosceles trapezium are equal.
\(CDEF\) is a trapezium with \(\hat{C} = 82^{\circ}\), \(\hat{E} = 142^{\circ}\), \(\hat{F} = 98^{\circ}\) and \(\hat{D} = 2p\). Determine the value of \(p\).
In trapezium \(CDEF\):
\[\begin{align} \hat{C} + \hat{D} + \hat{E} +\hat{F} &= 360^{\circ}\ (\text{sum of } \angle\text{s quad.}) \\ 82^{\circ} + 2p + 142^{\circ} + 98^{\circ} &= 360^{\circ} \\ 2p &= 360^{\circ} − 322^{\circ} \\ 2p &= 38^{\circ} \\ \therefore p &= 19^{\circ} \end{align}\]In trapezium \(CDEF\), \(p = 19^{\circ}\).
A kite is a quadrilateral with two pairs of adjacent sides equal. In kite \(ABCD\), the two shorter adjacent sides are equal, \(AD = CD\), and the two longer adjacent sides are equal, \(AB = CB\).
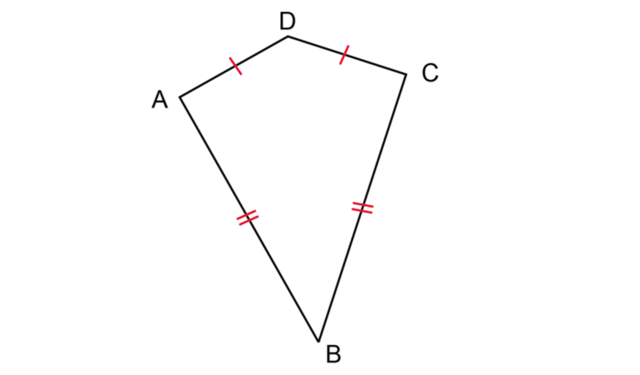
There is one pair of opposite angles that are equal.

\(ABCD\) is a kite with \(\hat{A} = 2z + 16^{\circ}\), \(\hat{D} = 103^{\circ}\), \(\hat{C} = z\), \(AD = AB\) and \(CD = CB\). Find the values of \(z\).
In kite \(ABCD\):
\[\begin{align} \hat{D} &= \hat{B} = 103^{\circ}\ (\text{opp. } \angle\text{s equal}) \\ \hat{A} + \hat{B} + \hat{C} + \hat{D} &= 360^{\circ}\ (\text{sum of } \angle\text{s quad.}) \\ 2z + 16^{\circ} + 103^{\circ} + z + 103^{\circ} &= 360^{\circ} \\ 3z &= 360^{\circ} − 222^{\circ} \\ 3z &= 138^{\circ} \\ \therefore z &= 46^{\circ} \end{align}\]In kite \(ABCD\), \(z = 46^{\circ}\).
Identify each shape.
Use the diagram to answer these questions.
Given: trapezium \(ABCD\) with \(AD \parallel BC\), \(\hat{A} = 86^{\circ}, \hat{B} = 150^{\circ}\) and \(\hat{D} = 94^{\circ}\). Find \(\hat{C}\).
Calculate the value of \(x\).
In kite \(ABCD\), \(AB = AD\) and \(BC = DC\). \(\hat{A} = 110^{\circ}, \hat{C} = 50^{\circ}\) and \(\hat{D} = \hat{B} = y\). Determine the value of \(y\).
Kite \(MNPQ\) has \(MN = NP\) and \(PQ = QM\). \(\hat{M} = 105^{\circ}\), \(\hat{P} = 105^{\circ}\) and \(\hat{Q} = 67^{\circ}\). Find \(\hat{N}\).
|
Previous
Classifying triangles
|
Table of Contents |
Next
Similar and congruent shapes
|