3.5 Solving problems with exponents and roots
We work with the power of \(3\) when we find the volume of a cube. To find the side of a cube if the volume is given, we need to take the cube root of the volume.
The volume of a cube is given by the formula
\[V = s^{3}\]where \(s\) is the side length of the cube.
Therefore, \(s = \sqrt[3]{V}\).
Worked example 3.9: Find the volume of a cube
Calculate the volume of the following cube. Round your answer to two decimal places.
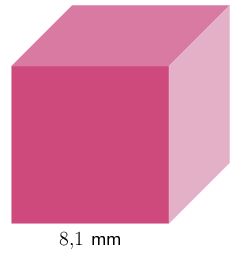
Use the formula for the volume of a cube.
\(V = s^{3}\)
Substitute the given side value, \(\mathbf {s = \text{8,1}}\).
\(V = (\text{8,1})^{3} = \text{531,441} \text{ mm}^{3}\)
Now, round the answer to two decimal places.
\(\text{531,44} \text{ mm}^{3}\)
Worked example 3.10: Find the volume of a cube
Given: the volume of a cube, \(V = 27 \text{ cm}^{3}\). Find the side of this cube, in centimetres.
To find the side of a cube with the given volume, we take the cube root of the volume:
\[s = \sqrt[3]{V}\]So, \(s = \sqrt[3]{27} = 3\text{ cm}\).
