End of chapter exercises
Calculate complementary and supplementary angles
-
Given line segment \(MN = 10 \text{ cm}\).
- Construct \(PQ\), the perpendicular bisector of \(MN\).
- Label point \(R\), the point of intersection of \(MN\) and \(PQ\).
- Measure and confirm that \(MR = RN\).
-
The diagrams below show the construction of a perpendicular bisector. The order of the diagrams is not correct. Study the diagrams and write down the correct order for constructing a perpendicular bisector of \(AB\).
- Diagram 1
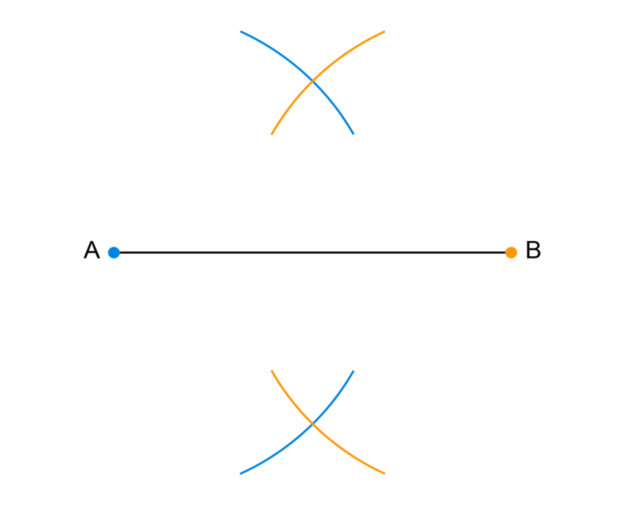
- Diagram 2
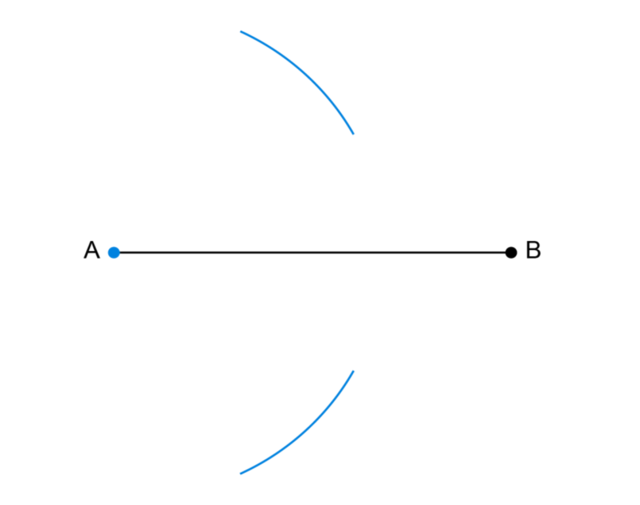
- Diagram 3
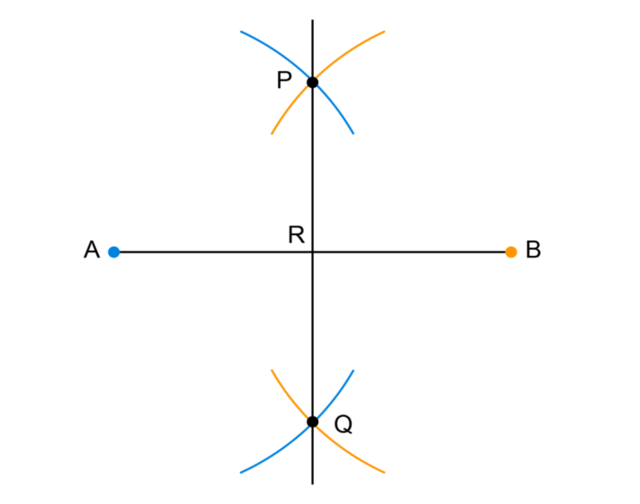
- Diagram 4

- Diagram 1
-
Draw \(\triangle ABC\). Choose any length for the sides of \(\triangle ABC\).
- Construct the perpendicular bisector of \(AB\).
- Construct the perpendicular bisector of \(BC\).
- What do you notice about these two lines?
- Construct the perpendicular bisector of \(CA\).
-
Use a ruler and a compass to construct \(\triangle DEF\) with \(DE = 10 \text{ cm}\), \(EF = 8 \text{ cm}\) and \(FD = 6 \text{ cm}\).
-
Show that the sum of interior angles of a rectangle is \(360^{\circ}\).
-
Use a ruler and a compass to construct \(\triangle STU\) with \(ST = 5 \text{ cm}\), \(TU = 4 \text{ cm}\) and \(US = 3 \text{ cm}\).
-
Answer these questions about complementary and supplementary angles.
- What is the complement of \(28^{\circ}\)?
- What is the complement of \(70^{\circ}\)?
- What is the supplement of \(62^{\circ}\)?
- What is the supplement of \(103^{\circ}\)?
-
Use a ruler and a compass to construct equilateral \(\triangle ABC\) with \(AB = 7 \text{ cm}\).
-
Use a compass and a ruler to construct square \(JKLM\) with \(JK = \text{6,5} \text{ cm}\).
-
Show that the sum of interior angles of a square is \(360^{\circ}\).
-
In quadrilateral \(QRST\) below, \(\hat{Q} = 84^{\circ}, \hat{S} = 105^{\circ}\) and \(\hat{T} = 65^{\circ}\). Determine the value of \(x\), giving a reason for your answer.
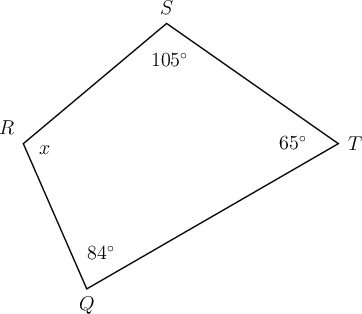
-
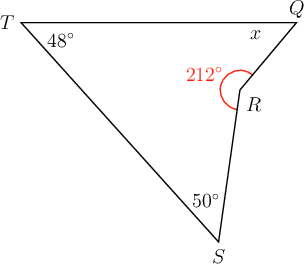
In quadrilateral \(QRST\)is given. \(\hat{R} = 212^{\circ}, \hat{S} = 50^{\circ}\) and \(\hat{T} = 48^{\circ}\). Find the value of \(x\), giving a reason for your answer.