16.8 Solving problems involving area and perimeter
Worked example 16.19: Solving problems involving areas of circles
Calculate the area of the shaded region. Use \(\pi = \text{3,14}\) for your calculations.
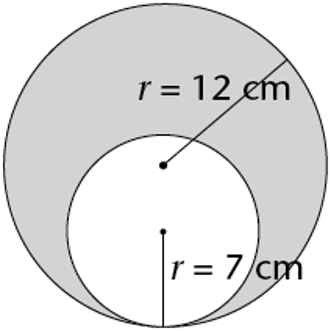
Calculate the area of the larger circle.
\[\begin{align} \text{Area of larger circle } &= \pi r^2 \\ &= \text{3,14}(12)^2 \\ &= \text{3,14}(144) \\ &= \text{452,16} \text{ cm}^2 \\ \end{align}\]Calculate the area of the smaller circle.
\[\begin{align} \text{Area of smaller circle } &= \pi r^2 \\ &= \text{3,14}(7)^2 \\ &= \text{3,14}(49) \\ &= \text{153,86}\text{ cm}^2 \end{align}\]Find the area of the shaded region.
\[\begin{align} \text{Area of the shaded region } &= \text{(area of larger circle)} − \text{(area of smaller circle)} \\ &= \text{452,16} \text{ cm}^2− \text{153,86} \text{ cm}^2 \\ &= \text{298,3} \text{ cm}^2 \end{align}\]Write the final answer.
\(\text{Area of shaded region } = \text{298,3} \text{ cm}^2\).
Worked example 16.20: Solving problems involving areas of circles and triangles
The diagram shows a circle and a right-angled triangle drawn within the circle. \(BC\) is a diameter of the circle. \(BC = 17 \text{ mm}\) and \(CD = 15 \text{ mm}\).
Determine the area of the shaded region. Use \(\pi = \frac{22}{7}\), and give your answer correct to two decimal places.
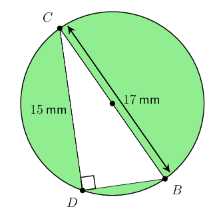
Calculate the area of the circle.
The diameter of the circle is \(BC = \text{17} \text{ mm}\), so we can divide by \(2\) to get the radius:
\[r = \frac{d}{2} = \frac{17}{2} = \text{8,5}\] \[\begin{align} \text{Area of circle } &= \pi r^2 \\ &= \pi (\text{8,5})^2 \\ &= \frac{22}{7} \times \text{72,25} \\ &= \text{227,07} \text{ mm}^2 \end{align}\]Calculate the area of the right-angled triangle.
\(CD = \text{15} \text{ mm}\) is the perpendicular height of the triangle. Since this is a right-angled triangle, we can use the theorem of Pythagoras to determine the length of the base of the triangle \(BD\).
In \(\triangle BCD\):
\[\begin{align} BD^2 + CD^2 &= BC^2 \text{ (Pythagoras)} \\ BD^2 + 15^2 &= 17^2 \\ BD^2 &= 289 − 225 \\ BD^2 &= 64 \\ \therefore BD &= 8 \end{align}\]So base \(BD = 8 \text{ mm}\)
We can now calculate the area of the triangle \(\triangle BCD\):
\[\begin{align} \text{Area } \triangle BCD &= \frac{1}{2}(b \times h) \\ &= \frac{1}{2}(8 \times 15) \\ &= \frac{1}{2}(120) \\ &= 60 \text{ mm}^2 \end{align}\]Calculate the area of the shaded region.
\[\begin{align} \text{Area of the shaded region } &= \text{(area of circle)} − \text{(area of triangle)} \\ &= \text{227,07} \text{ mm}^2 – 60 \text{ mm}^2 \\ &= \text{167,07} \text{ mm}^2 \end{align}\]Write the final answer.
Area of the shaded region \(= \text{167,07} \text{ mm}^2\).
