1.1 Arithmetic sequences
|
Next
1.2 Geometric sequences
|
Chapter 1: Sequences and series
- Discuss and explain important terminology.
- Be consistent with the use of “common” difference and “constant” ratio to avoid confusing learners.
- Learners must understand the difference between arithmetic and geometric sequences.
- Explain sigma notation carefully as many learners have difficulty with this concept.
- Encourage learners to use the correct notation (for example \(T_{n}, \enspace S_{n}\) etc.) when solving problems.
- Use the investigation for the sum of an infinite series to introduce the concept of convergence and divergence.
In earlier grades we learnt about number patterns, which included linear sequences with a common difference and quadratic sequences with a common second difference. We also looked at completing a sequence and how to determine the general term of a sequence.
In this chapter we also look at geometric sequences, which have a constant ratio between consecutive terms. We will learn about arithmetic and geometric series, which are the summing of the terms in sequences.
1.1 Arithmetic sequences (EMCDP)
An arithmetic sequence is a sequence where consecutive terms are calculated by adding a constant value (positive or negative) to the previous term. We call this constant value the common difference (\(d\)).
For example,
\[\text{3}; \text{0}; -\text{3}; -\text{6}; -\text{9}; \ldots\]This is an arithmetic sequence because we add \(-\text{3}\) to each term to get the next term:
|
First term |
\(T_{1}\) |
\(\text{3}\) |
|
|
Second term |
\(T_{2}\) |
\(3 + (-3) =\) |
\(0\) |
|
Third term |
\(T_{3}\) |
\(0 + (-3) =\) |
\(-\text{3}\) |
|
Fourth term |
\(T_{4}\) |
\(-3 + (-3) =\) |
\(-\text{6}\) |
|
Fifth term |
\(T_{5}\) |
\(-6 + (-3) =\) |
\(-\text{9}\) |
|
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
Arithmetic sequences
Find the common difference and write down the next \(\text{3}\) terms of the sequence.
This is an example of a non-numeric arithmetic sequence.
\begin{align*} d &= (a-b) - (a-3b) \\ &= a-b-a+3b \\ &= 2b \\ \text{ or } & \\ d &= (a+b) - (a-b) \\ &= a+b -a +b \\ &= 2b \\ \therefore T_{7} &= a + 3b + 2b \\ &= a+ 5b \\ T_{8} &= a+5b + 2b \\ &= a + 7b \\ T_{9} &= a + 7b +2b \\ &= a + 9b \end{align*}The general term for an arithmetic sequence (EMCDQ)
For a general arithmetic sequence with first term \(a\) and a common difference \(d\), we can generate the following terms:
\begin{align*} {T}_{1}&= a \\ {T}_{2}&= {T}_{1}+d = a + d \\ {T}_{3}&= {T}_{2}+d = \left(a+d\right)+d =a+2d \\ {T}_{4}&= {T}_{3}+d=\left(a+2d\right)+d=a+3d \\ \vdots & \quad \quad \qquad \vdots \quad \quad \qquad \vdots \quad \quad \qquad \vdots \\ {T}_{n}&= {T}_{n-1} + d =\left(a+(n-2)d\right)+d = a + \left(n-1\right)d \end{align*}Therefore, the general formula for the \(n\)\(^{\text{th}}\) term of an arithmetic sequence is:
\[{T}_{n}= a + \left(n-1\right)d\]- Arithmetic sequence
-
An arithmetic (or linear) sequence is an ordered set of numbers (called terms) in which each new term is calculated by adding a constant value to the previous term:
\[{T}_{n}=a+(n-1)d\]where
-
\({T}_{n}\) is the \(n\)\(^{\text{th}}\) term;
-
\(n\) is the position of the term in the sequence;
-
\(a\) is the first term;
-
\(d\) is the common difference.
-
Test for an arithmetic sequence
To test whether a sequence is an arithmetic sequence or not, check if the difference between any two consecutive terms is constant:
\[d = {T}_{2}-{T}_{1}={T}_{3}-{T}_{2}= \ldots = {T}_{n}-{T}_{n-1}\]If this is not true, then the sequence is not an arithmetic sequence.
Worked example 1: Arithmetic sequence
Given the sequence \(-15; -11; -7; \ldots 173\).
- Is this an arithmetic sequence?
- Find the formula of the general term.
- Determine the number of terms in the sequence.
Check if there is a common difference between successive terms
\begin{align*} T_{2} - T_{1} &= -11 - (-15) = 4 \\ T_{3} - T_{2} &= -7 - (-11) = 4 \\ \therefore \text{This is an } & \text{arithmetic sequence with } d = 4 \end{align*}Determine the formula for the general term
Write down the formula and the known values:
\[T_{n} = a + (n-1)d\] \[a = -15; \qquad d = 4\] \begin{align*} T_{n} &= a + (n-1)d \\ &= -15 + (n-1)(4) \\ &= -15 + 4n - 4 \\ &= 4n - 19 \end{align*}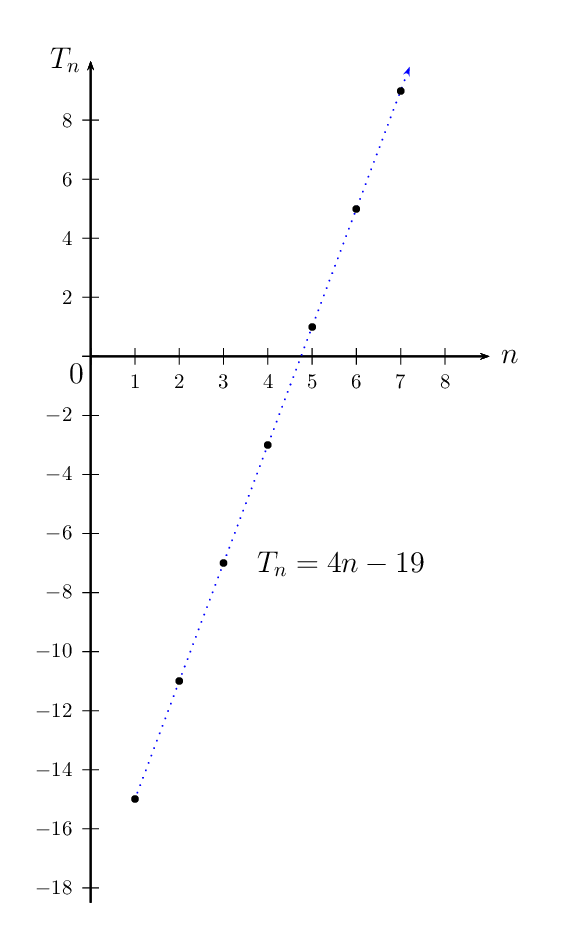
A graph was not required for this question but it has been included to show that the points of the arithmetic sequence lie in a straight line.
Note: The numbers of the sequence are natural numbers \(\left(n \in \{1;2;3; \ldots \} \right)\) and therefore we should not connect the plotted points. In the diagram above, a dotted line has been used to show that the graph of the sequence lies on a straight line.
Determine the number of terms in the sequence
\begin{align*} T_{n} &= a + (n-1)d \\ 173 &= 4n - 19 \\ 192 &= 4n \\ \therefore n &= \frac{192}{4} \\ &= 48 \\ \therefore T_{48} &= 173 \end{align*}Write the final answer
Therefore, there are \(\text{48}\) terms in the sequence.
Arithmetic mean
The arithmetic mean between two numbers is the number half-way between the two numbers. In other words, it is the average of the two numbers. The arithmetic mean and the two terms form an arithmetic sequence.
For example, the arithmetic mean between \(\text{7}\) and \(\text{17}\) is calculated:
\begin{align*} \text{Arithmetic mean } &= \frac{7 + 17}{2} \\ &= 12 \\ \therefore 7; 12; 17 & \text{ is an arithmetic sequence} \\ T_{2} - T_{1} &= 12 - 7 = 5 \\ T_{3} - T_{2} &= 17-12 = 5 \end{align*}Plotting a graph of the terms of a sequence sometimes helps in determining the type of sequence involved. For an arithmetic sequence, plotting \({T}_{n}\) vs. \(n\) results in the following graph:
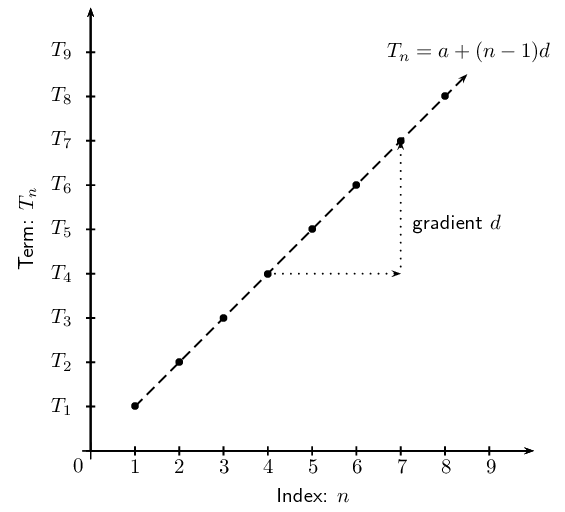
- If the sequence is arithmetic, the plotted points will lie in a straight line.
- Arithmetic sequences are also called linear sequences, where the common difference (\(d\)) is the gradient of the straight line.
Arithmetic Sequences
Given the sequence \(7; \text{5,5}; 4; \text{2,5}; \ldots\)
Given the sequence \(2; 6; 10; 14; \ldots\)
Yes, this is an arithmetic sequence since there is a common difference of \(\text{4}\) between consecutive terms.
This value of \(n\) is not a positive integer, therefore \(\text{1 204}\) is not a term of this sequence.
An arithmetic sequence has the general term \(T_{n} = -2n + 7\).
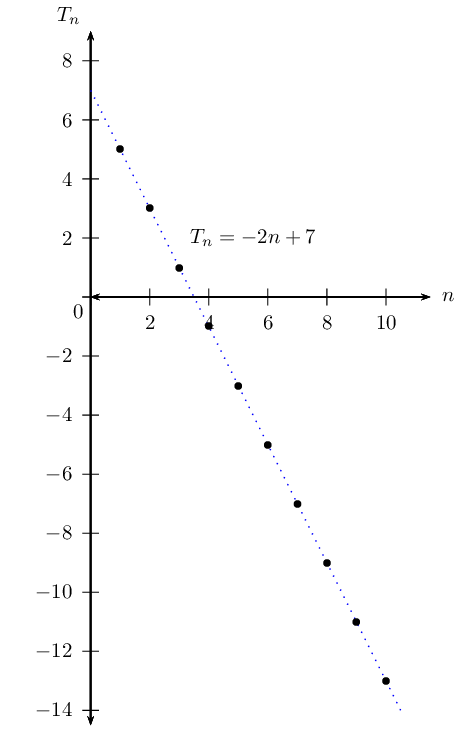
Calculate the common difference \((d)\):
\begin{align*} a & = -\frac{1}{2} \\ \text{General formula: } T_{n} &= a + (n-1)d \\ T_{22} &= -\frac{1}{2} + (22 - 1)d \\ \therefore 10 &= -\frac{1}{2} + 21d \\ 10 + \frac{1}{2} &= 21d \\ \frac{21}{2} &= 21d \\ \therefore d &= \frac{1}{2} \end{align*}Now determine the general term for the sequence:
\begin{align*} T_{n} &= a + (n - 1)d \\ T_{n} &= -\frac{1}{2} + (n-1) \left( \frac{1}{2} \right)\\ &= -\frac{1}{2} + \frac{1}{2}n -\frac{1}{2} \\ \therefore T_{n} &= \frac{1}{2}n - 1 \end{align*}What are the important characteristics of an arithmetic sequence?
- There is a common difference between any two successive terms in the sequence.
- The graph of \(T_{n}\) vs. \(n\) is a straight line.
You are given the first four terms of an arithmetic sequence. Describe the method you would use to find the formula for the \(n\)\(^{\text{th}}\) term of the sequence.
- Use the given terms to calculate the common difference \((d): \quad d = T_{2} - T_{1}\).
- From given terms, we know that \(T_{1} = a\).
- Substitute the values for \(a\) and \(d\) into the equation \(T_{n} = a + (n-1)d\).
- Simplify and gather like \(n\) terms.
A single square is made from \(\text{4}\) matchsticks. To make two squares in a row takes \(\text{7}\) matchsticks, while three squares in a row takes \(\text{10}\) matchsticks.
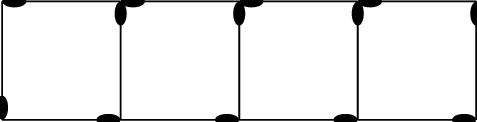
Write down the first four terms of the sequence.
What is the common difference?
Determine the formula for the general term.
How many matchsticks are in a row of \(\text{25}\) squares?
If there are \(\text{109}\) matchsticks, calculate the number of squares in the row.
A pattern of equilateral triangles decorates the border of a girl's skirt. Each triangle is made by three stitches, each having a length of \(\text{1}\) \(\text{cm}\).
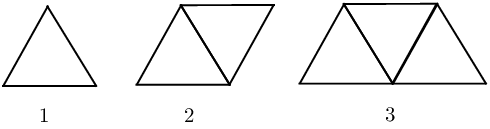
Complete the table:
| Figure no. | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(q\) | \(r\) | \(n\) |
| No. of stitches | \(\text{3}\) | \(\text{5}\) | \(p\) | \(\text{15}\) | \(\text{71}\) | \(s\) |
The terms \(p; (2p+2); (5p+3)\) form an arithmetic sequence. Find \(p\) and the \(15^{\text{th}}\) term of the sequence.
[IEB, Nov 2011]
The arithmetic mean of \(3a - 2\) and \(x\) is \(4a-4\). Determine the value of \(x\) in terms of \(a\).
Insert seven arithmetic means between the terms \((3s-t)\) and \((-13s+7t)\).
Let the arithmetic means be:
\(a_{1}; a_{2}; a_{3}; a_{4}; a_{5}; a_{6}; a_{7}\)Therefore the sequence is:
\[T_{1}; a_{1}; a_{2}; a_{3}; a_{4}; a_{5}; a_{6}; a_{7}; T_{9}\] \begin{align*} T_{1} &= 3s-t \\ T_{9} &= -13s + 7t \\ d &= \frac{T_{9} - T_{1}}{8} \\ &= \frac{-13s + 7t -3s + t}{8} \\ &= \frac{-16s + 8t}{8} \\ &= -2s + t \\ \therefore T_{1} &= 3s -t \\ a_{1} &= (3s - t) +(-2s + t) \\ &= s \\ a_{2} &= (s) +(-2s + t) \\ &= -s + t \\ a_{3} &= (-s + t) +(-2s + t) \\ &= -3s + 2t \\ a_{4} &= (-3s + 2t) +(-2s + t) \\ &= -5s + 3t \\ a_{5} &= (-5s + 3t) +(-2s + t) \\ &= -7s + 4t \\ a_{6} &= (-7s + 4t) +(-2s + t) \\ &= -9s + 5t \\ a_{7} &= (-9s + 5t) +(-2s + t) \\ &= -11s + 6t \\ T_{9} &= (-11s + 6t) +(-2s + t)\\ &= -13s + 7t \end{align*}- Quadratic sequence
-
A quadratic sequence is a sequence of numbers in which the second difference between any two consecutive terms is constant.
The general formula for the \(n^{\text{th}}\) term of a quadratic sequence is: \[{T}_{n}=a{n}^{2}+bn+c\]
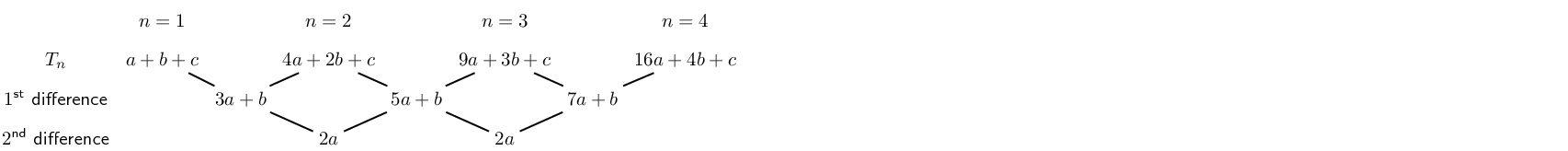
It is important to note that the first differences of a quadratic sequence form an arithmetic sequence. This sequence has a common difference of \(2a\) between consecutive terms. In other words, a linear sequence results from taking the first differences of a quadratic sequence.
Worked example 2: Quadratic sequence
Consider the pattern of white and blue blocks in the diagram below.
- Determine the sequence formed by the white blocks \((w)\).
- Find the sequence formed by the blue blocks \((b)\).
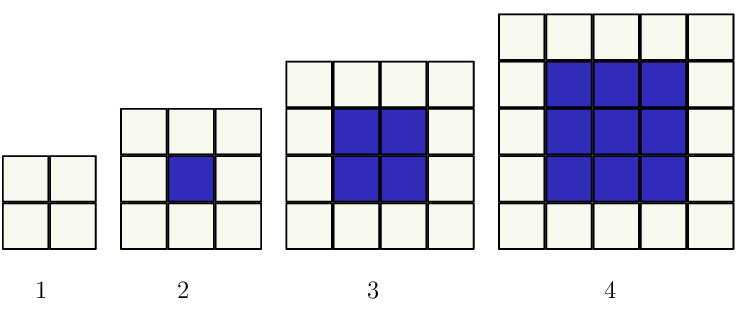
| Pattern number \((n)\) | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{5}\) | \(\text{6}\) | \(n\) |
| No. of white blocks \((w)\) | |||||||
| Common difference \((d)\) |
| Pattern number \((n)\) | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{5}\) | \(\text{6}\) | \(n\) |
| No. of blue blocks \((b)\) | |||||||
| Common difference \((d)\) |
Use the diagram to complete the table for the white blocks
| Pattern number \((n)\) | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{5}\) | \(\text{6}\) | \(n\) |
| No. of white blocks \((w)\) | \(\text{4}\) | \(\text{8}\) | \(\text{12}\) | \(\text{16}\) | \(\text{20}\) | \(\text{24}\) | \(4n\) |
| Common difference \((d)\) | \(\text{4}\) | \(\text{4}\) | \(\text{4}\) | \(\text{4}\) | \(\text{4}\) |
We see that the next term in the sequence is obtained by adding \(\text{4}\) to the previous term, therefore the sequence is linear and the common difference \((d)\) is \(\text{4}\).
The general term is:
\begin{align*} T_{n} &= a + (n-1)d \\ &= 4 + (n-1)(4) \\ &= 4 + 4n - 4 \\ &= 4n \end{align*}Use the diagram to complete the table for the blue blocks
| Pattern number \((n)\) | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{5}\) | \(\text{6}\) |
| No. of blue blocks \((b)\) | \(\text{0}\) | \(\text{1}\) | \(\text{4}\) | \(\text{9}\) | \(\text{16}\) | \(\text{25}\) |
| Difference | \(\text{1}\) | \(\text{3}\) | \(\text{5}\) | \(\text{7}\) | \(\text{9}\) |
We notice that there is no common difference between successive terms. However, there is a pattern and on further investigation we see that this is in fact a quadratic sequence:
| Pattern number \((n)\) | \(\text{1}\) | \(\text{2}\) | \(\text{3}\) | \(\text{4}\) | \(\text{5}\) | \(\text{6}\) | \(n\) |
| No. of blue blocks \((b)\) | \(\text{0}\) | \(\text{1}\) | \(\text{4}\) | \(\text{9}\) | \(\text{16}\) | \(\text{25}\) | \((n-1)^{2}\) |
| First difference | \(-\) | \(\text{1}\) | \(\text{3}\) | \(\text{5}\) | \(\text{7}\) | \(\text{9}\) | \(-\) |
| Second difference | \(-\) | \(-\) | \(\text{2}\) | \(\text{2}\) | \(\text{2}\) | \(\text{2}\) | \(-\) |
| Pattern | \((1-1)^{2}\) | \((2-1)^{2}\) | \((3-1)^{2}\) | \((4-1)^{2}\) | \((5-1)^{2}\) | \((6-1)^{2}\) | \((n-1)^{2}\) |
Draw a graph of \(T_{n}\) vs. \(n\) for each sequence
\begin{align*} \text{White blocks: } T_{n} &= 4n \\ \text{Blue blocks: } T_{n} &= (n-1)^{2} \\ &= n^{2} - 2n + 1 \end{align*}
Since the numbers of the sequences are natural numbers \(\left(n \in \{1;2;3; \ldots \} \right)\), we should not connect the plotted points. In the diagram above, a dotted line has been used to show that the graph of the sequence formed by the white blocks \((w)\) is a straight line and the graph of the sequence formed by the blue blocks \((b)\) is a parabola.
Quadratic sequences
Determine whether each of the following sequences is:
- a linear sequence;
- a quadratic sequence;
- or neither.
\(8;17;32;53;80;\ldots\)
Quadratic sequence
\(3p^2; 6p^2; 9p^2; 12p^2; 15p^2; \ldots\)
Linear sequence
\(1;\text{2,5};5;\text{8,5};13;\ldots\)
Quadratic sequence
\(2;6;10;14;18;\ldots\)
Linear sequence
\(5;19;41;71;109;\ldots\)
Quadratic sequence
\(3;9;16;21;27;\ldots\)
Neither
\(2k; 8k; 18k; 32k; 50k; \ldots\)
Quadratic sequence
\(2\frac{1}{2}; 6; 10\frac{1}{2}; 16; 22\frac{1}{2}; \ldots\)
Quadratic sequence
A quadratic pattern is given by \(\; T_{n} = n^{2} + bn + c\). Find the values of \(b\) and \(c\) if the sequence starts with the following terms: \[-1 \; ; \; 2 \; ; \; 7 \; ; \; 14 \; ; \; \ldots\]
Starting with the first term, we have \(n = 1\) and \(T_{1} = -1\): \begin{align*} T_{1} & = (1)^{2} + b(1) + c \\ (-1) & = 1 + b + c \\ -2 & = b + c \end{align*}
For the second term, we use \(n = 2\) and \(T_{2} = 2\):
\begin{align*} T_{2} & = (2)^{2} + b(2) + c \\ (2) & = 4 + 2 b + c \\ -2 & = 2 b + c \end{align*}Now we must solve these equations simultaneously. We can do this by substitution, but here we will show the solution using the 'elmination' method (which means subtracting one equation from the other to cancel the \(c\)'s).
\begin{align*} -2 & = 2 b + c \\ - ( -2 & = \; b + c ) \\ 0 & = \; b \end{align*}Finally, calculate the value of \(c\). As usual for simultaneous equations, this means that we must substitute the \(b = 0\) into either of the equations we used above. Let's use the equation \(-2 = b + c\).
\begin{align*} b = 0 \; \longrightarrow \quad -2 & = b + c \\ -2 & = ( 0 ) + c \\ -2 & = \; c \end{align*}The final answers are \(b = 0\) and \(c = -2\).
NOTE: Now we know that the general term of the sequence is \(\; T_{n} = n^{2} - 2 \;\). We can use this to check our answers. We know that \(T_{3} = 7\). Substitute \(n = 3\) into the general formula to check:
\begin{align*} T_{n} & = n^{2} - 2 \\ T_{3} & = (3)^{2} - 2 \\ & = (9) +0 -2 \\ & = 7 \end{align*}\(a^{2}; -a^{2}; -3a^{2}; -5a^{2}; \ldots\) are the first \(\text{4}\) terms of a sequence.
This is an arithmetic sequence since there is a common difference of \(-2a^{2}\) between consecutive terms.
Given \(\; T_{n} = n^{2} + bn + c\), determine the values of \(b\) and \(c\) if the sequence starts with the terms: \[2 \; ; \; 7 \; ; \; 14 \; ; \; 23 \; ; \; \ldots\]
Starting with the first term, we have \(n = 1\) and \(T_{1} = 2\): \begin{align*} T_{1} & = (1)^{2} + b(1) + c \\ (2) & = 1 + b + c \\ 1 & = b + c \end{align*}
For the second term, we use \(n = 2\) and \(T_{2} = 7\): \begin{align*} T_{2} & = (2)^{2} + b(2) + c \\ (7) & = 4 + 2 b + c \\ 3 & = 2 b + c \end{align*}
Now we must solve these equations simultaneously. We can do this by substitution, but here we will show the solution using the 'elimination' method (which means subtracting one equation from the other to cancel the \(c\)'s). \begin{align*} 3 & = 2 b + c \\ - ( 1 & = \; b + c ) \\ 2 & = \; b \end{align*}
Finally, calculate the value of \(c\). As usual for simultaneous equations, this means that we must substitute the \(b = 2\) into either of the equations we used above. Let's use the equation \(1 = b + c\). \begin{align*} b = 2 \; \longrightarrow \quad 1 & = b + c \\ 1 & = ( 2 ) + c \\ -1 & = \; c \end{align*} The final answers are \(b = 2\) and \(c = -1\).
NOTE: Now we know that the general term of the sequence is \(\; T_{n} = n^{2} + 2 n - 1 \;\). We can use this to check our answers. We know that \(T_{3} = 14\). Substitute \(n = 3\) into the general formula to check:
\begin{align*} T_{n} & = n^{2} + 2 n - 1 \\ T_{3} & = (3)^{2} + 2 (3) - 1 \\ & = (9) +6 -1 \\ & = 14 \end{align*}The first term of a quadratic sequence is \(\text{4}\), the third term is \(\text{34}\) and the common second difference is \(\text{10}\). Determine the first six terms in the sequence.
\(4; 14; 34; 64; 104; 154\)
A quadratic sequence has a second term equal to \(\text{1}\), a third term equal to \(-\text{6}\) and a fourth term equal to \(-\text{14}\).
Determine the second difference for this sequence.
Hence, or otherwise, calculate the first term of the pattern.
| Table of Contents |
Next
1.2 Geometric sequences
|
