2.5 Quadratic functions
|
Previous
2.4 Linear functions
|
Next
2.6 Exponential functions
|
2.5 Quadratic functions (EMCFC)
Inverse of the function \(y=a{x}^{2}\) (EMCFD)
Worked example 6: Inverse of the function \(y=a{x}^{2}\)
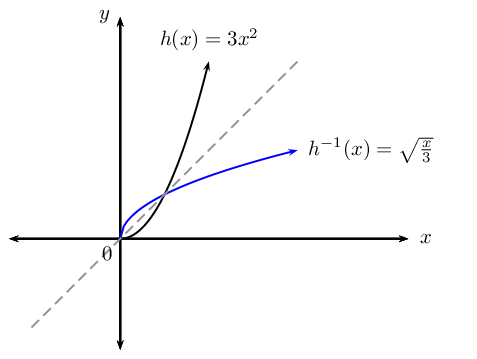
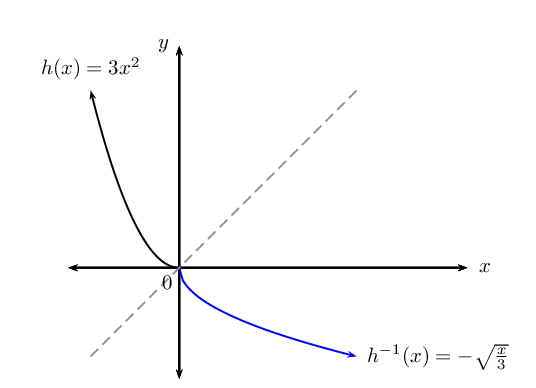
Determine the inverse of the quadratic function \(h(x) = 3x^{2}\) and sketch both graphs on the same system of axes.
Determine the inverse of the given function \(h(x)\)
- Interchange \(x\) and \(y\) in the equation.
- Make \(y\) the subject of the new equation.
Sketch the graphs on the same system of axes
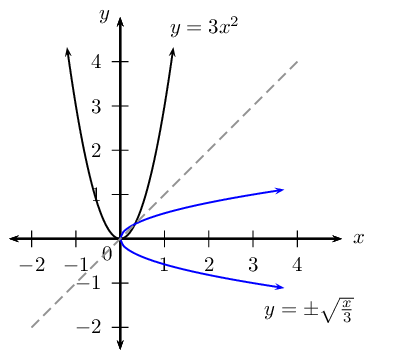
Notice that the inverse does not pass the vertical line test and therefore is not a function.
To determine the inverse function of \(y=ax^{2}\):
\[\begin{array}{rll} &(1) \quad \text{Interchange } x \text{ and } y: & x = ay^{2} \\ &(2) \quad \text{Make } y \text{ the subject of the equation}: & \frac{x}{a} = y^{2} \\ &&\therefore y = ±\sqrt{\frac{x}{a}} \qquad (x \geq 0) \end{array}\]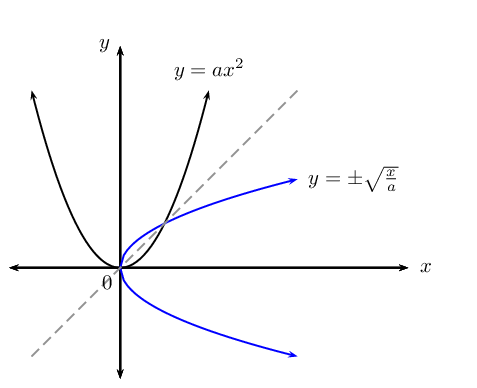
The vertical line test shows that the inverse of a parabola is not a function. However, we can limit the domain of the parabola so that the inverse of the parabola is a function.
Domain and range
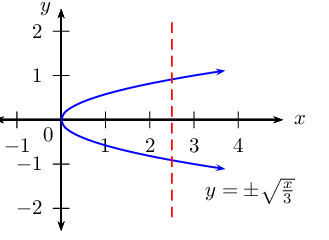
Consider the previous worked example \(h(x) = 3x^{2}\) and its inverse \(y = ±\sqrt{\frac{x}{3}}\):
-
If we restrict the domain of \(h\) so that \(x\ge 0\), then \(h^{-1}(x) = \sqrt{\frac{x}{3}}\) passes the vertical line test and is a function.
-
If the restriction on the domain of \(h\) is \(x\le 0\), then \(h^{-1}(x) = -\sqrt{\frac{x}{3}}\) would also be a function.
The domain of the function is equal to the range of the inverse. The range of the function is equal to the domain of the inverse.
Similarly, a restriction on the domain of the function results in a restriction on the range of the inverse and vice versa.

Worked example 7: Inverses - domain, range and restrictions
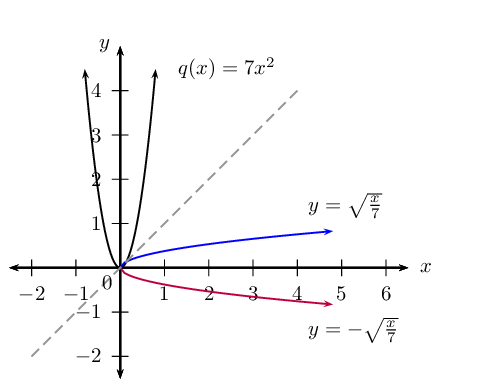
Determine the inverse of \(q(x) = 7x^{2}\) and sketch both graphs on the same system of axes. Restrict the domain of \(q\) so that the inverse is a function.
Examine the function and determine the inverse
Determine the inverse of the function:
\begin{align*} \text{Let } y & = 7x^{2} \\ \text{Interchange } x \text{ and } y: \quad x & = 7y^{2} \\ \frac{x}{7} & = y^{2} \\ \therefore y & = ±\sqrt{\frac{x}{7}} \qquad (x \geq 0) \end{align*}Sketch both graphs on the same system of axes
Determine the restriction on the domain
Option \(\text{1}\): Restrict the domain of \(q\) to \(x \ge 0\) so that the inverse will also be a function \(\left( q^{-1} \right)\). The restriction \(x \ge 0\) on the domain of \(q\) will restrict the range of \(q^{-1}\) such that \(y \ge 0\).
\begin{align*} q: \qquad & \text{domain } x \ge 0 \quad \text{range } y \ge 0 \\ q^{-1}: \qquad & \text{domain } x \ge 0 \quad \text{range } y \ge 0 \end{align*}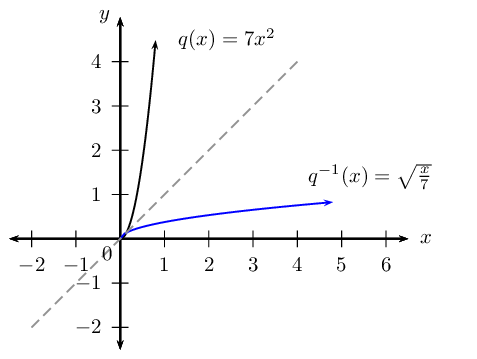
or
Option \(\text{2}\): Restrict the domain of \(q\) to \(x \le 0\) so that the inverse will also be a function \(\left( q^{-1} \right)\). The restriction \(x \le 0\) on the domain of \(q\) will restrict the range of \(q^{-1}\) such that \(y \le 0\).
\begin{align*} q: \qquad & \text{domain } x \le 0 \quad \text{range } y \ge 0 \\ q^{-1}: \qquad & \text{domain } x \ge 0 \quad \text{range } y \le 0 \end{align*}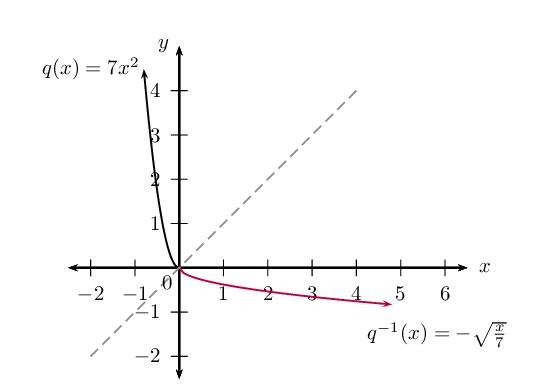
Worked example 8: Inverses - domain, range and restrictions
- Determine the inverse of \(f(x) = -x^{2}\).
- Sketch both graphs on the same system of axes.
- Restrict the domain of \(f\) so that its inverse is a function.
Determine the inverse of the function
\begin{align*} \text{Let } y & = -x^{2} \\ \text{Interchange } x \text{ and } y: \quad x & = -y^{2} \\ -x & = y^{2} \\ y & = ±\sqrt{-x} \qquad (x \leq 0) \end{align*}Note: \(\sqrt{-x}\) is only defined if \(x \le 0\).
Sketch both graphs on the same system of axes
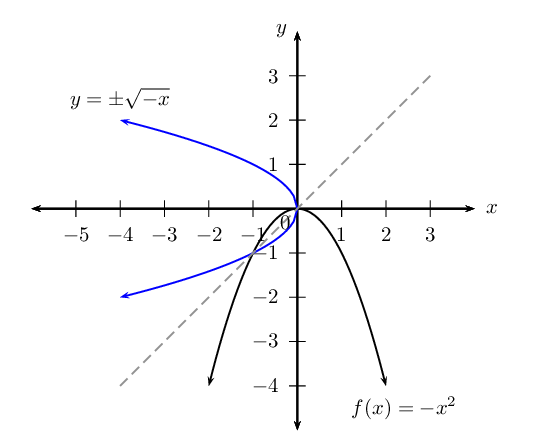
The inverse does not pass the vertical line test and is not a function.
Determine the restriction on the domain
- If \(f(x) = -x^{2}, \text{ for } x \le 0\): \begin{align*} f: \qquad & \text{domain } x \le 0 \quad \text{range } y \le 0 \\ f^{-1}: \qquad & \text{domain } x \le 0 \quad \text{range } y \le 0 \end{align*}
- If \(f(x) = -x^{2}, \text{ for } x \ge 0\): \begin{align*} f: \qquad & \text{domain } x \ge 0 \quad \text{range } y \le 0 \\ f^{-1}: \qquad & \text{domain } x \le 0 \quad \text{range } y \ge 0 \end{align*}
Inverses - domain, range, intercepts, restrictions
Determine the inverse for each of the following functions:
Given the function \(g(x) = \frac{1}{2}x^{2}\) for \(x \ge 0\).
Find the inverse of \(g\).
Draw \(g\) and \(g^{-1}\) on the same set of axes.
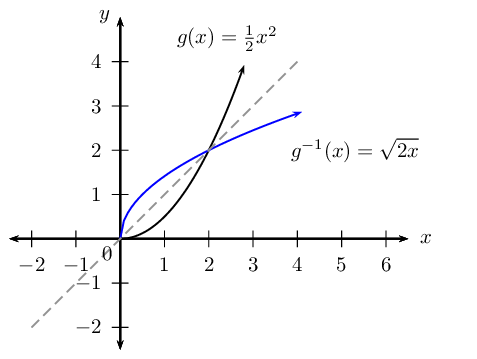
Is \(g^{-1}\) a function? Explain your answer.
Yes. It passes the vertical line test and is a one-to-one relation.
State the domain and range for \(g\) and \(g^{-1}\).
Determine the coordinates of the point(s) of intersection of the function and its inverse.
To find the points of intersection, we equate \(g(x)\) and \(g^{-1}(x)\):
\begin{align*} \frac{1}{2}x^{2} & = \sqrt{2x} \\ \left( \frac{1}{2}x^{2} \right)^{2} & = \left( \sqrt{2x} \right)^{2} \\ \frac{1}{4}x^{4} & = 2x \\ x^{4} & = 8x \\ x^{4} - 8x & = 0\\ x(x^{3} - 8) & = 0\\ x(x-2)(x^{2} + 2x + 4) & = 0\\ \therefore x = 0 \text{ or } x =2 \text{ or } & x^{2} + 2x + 4 = 0 \end{align*} \begin{align*} \text{If } x & = 0 \\ y & = 0 \\ \text{If } x & = 2 \\ y & = \frac{1}{2}(2)^{2} \\ & = 2 \end{align*} \begin{align*} \text{If } x^{2} + 2x + 4 & = 0 \\ \text{Use the quadratic formula } x & = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a} \\ & = \frac{-2 \pm \sqrt{(2)^{2} - 4(1)(4)}}{2(1)} \\ & = \frac{-2 \pm \sqrt{-12}}{2} \\ & = \text{no real solution} \end{align*}Therefore, we get the points \((0;0)\) or \((2;2)\).
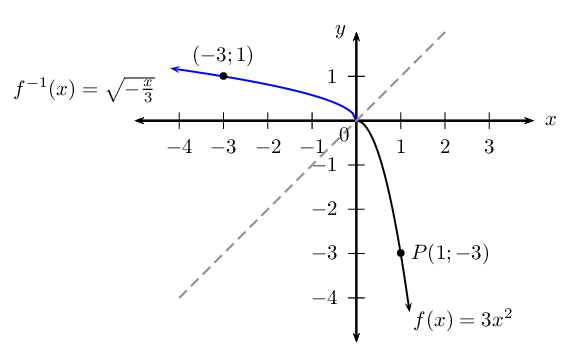
Given the graph of the parabola \(f(x) = ax^{2}\) with \(x \ge 0\) and passing through the point \(P(1;-3)\).
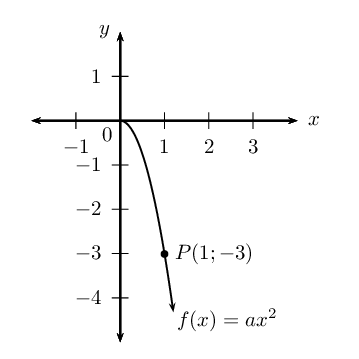
Determine the equation of the parabola.
State the domain and range of \(f\).
Give the coordinates of the point on \(f^{-1}\) that is symmetrical to the point \(P\) about the line \(y=x\).
Determine the equation of \(f^{-1}\).
State the domain and range of \(f^{-1}\).
Draw a graph of \(f^{-1}\).
Determine the inverse of \(h(x) = \frac{11}{5}x^{2}\).
Sketch both graphs on the same system of axes.
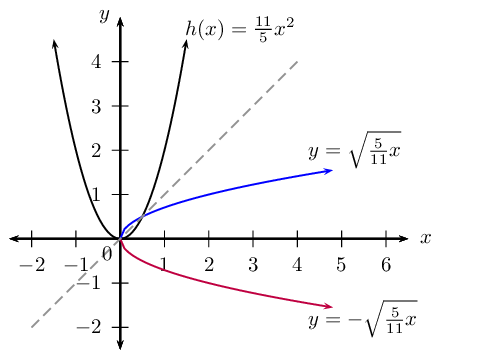
Restrict the domain of \(h\) so that the inverse is a function.
Option \(\text{1}\): Restrict the domain of \(h\) to \(x \ge 0\) so that the inverse will also be a function \(\left( h^{-1} \right)\). The restriction \(x \ge 0\) on the domain of \(h\) will restrict the range of \(h^{-1}\) such that \(y \ge 0\).
\begin{align*} h: \qquad & \text{domain } x \ge 0 \quad \text{range } y \ge 0 \\ h^{-1}: \qquad & \text{domain } x \ge 0 \quad \text{range } y \ge 0 \end{align*}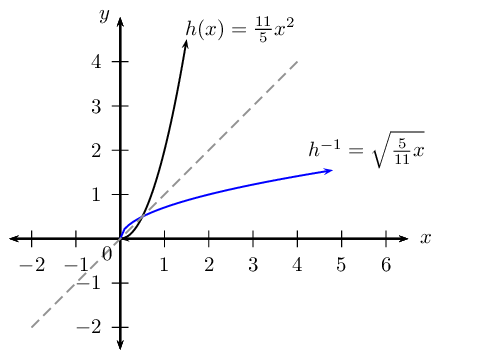
or
Option \(\text{2}\): Restrict the domain of \(h\) to \(x \le 0\) so that the inverse will also be a function \(\left( h^{-1} \right)\). The restriction \(x \le 0\) on the domain of \(h\) will restrict the range of \(h^{-1}\) such that \(y \le 0\).
\begin{align*} h: \qquad & \text{domain } x \le 0 \quad \text{range } y \ge 0 \\ h^{-1}: \qquad & \text{domain } x \ge 0 \quad \text{range } y \le 0 \end{align*}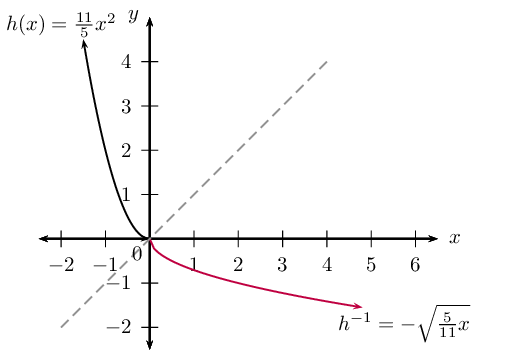
The diagram shows the graph of \(g(x) = mx + c\) and \(f^{-1}(x) = a \sqrt{x}, \enspace (x \geq 0)\). Both graphs pass through the point \(P(4;-1)\).
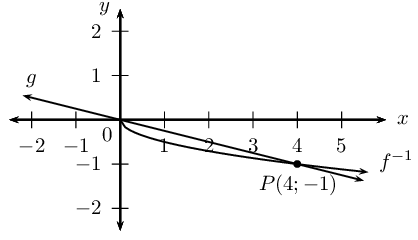
Determine the values of \(a\), \(c\) and \(m\).
From the graph we see that the straight line passes through the origin, therefore \(c=0\).
\begin{align*} g(x) & = mx \\ \text{Substitute } P(4;-1): \enspace -1 & = 4m \\ \therefore m & = - \frac{1}{4} \\ \therefore g(x) & = - \frac{1}{4} x \\ & \\ f^{-1}(x)& = a \sqrt{x} \\ \text{Substitute } P(4;-1): \enspace -1 & = a \sqrt{4} \\ -1 & = 2a \\ \therefore a & = - \frac{1}{2} \\ \therefore f^{-1}(x) & = - \frac{1}{2} \sqrt{x} \end{align*}Give the domain and range of \(f^{-1}\) and \(g\).
For which values of \(x\) is \(g(x) < f(x)\)?
Determine \(f\).
Determine the coordinates of the point(s) of intersection of \(g\) and \(f\) intersect.
To determine the coordinates of the point(s) of intersection, we equate \(g\) and \(f\):
\begin{align*} - \frac{1}{4} x & = 4x^{2} \\ 0 & = 4x^{2} + \frac{1}{4} x \\ 0 & = x \left(4x + \frac{1}{4} \right) \\ \therefore x = 0 & \text{ or } 4x + \frac{1}{4} = 0 \\ \text{If } x = 0: \enspace y &= 0 \\ \text{If } 4x + \frac{1}{4} &= 0: \\ 4x &= - \frac{1}{4} \\ x &= - \frac{1}{16} \\ \text{If } x = - \frac{1}{16}: \enspace y &= - \frac{1}{4} \left( - \frac{1}{16} \right) \\ &= \frac{1}{64} \end{align*}Therefore, the two graphs intersect at \(\left( 0;0 \right)\) and \(\left( - \frac{1}{16}; \frac{1}{64} \right)\).
Worked example 9: Inverses - average gradient
Given: \(h(x) = 2x^{2}, \quad x \ge 0\)
- Determine the inverse, \(h^{-1}\).
- Find the point where \(h\) and \(h^{-1}\) intersect.
- Sketch \(h\) and \(h^{-1}\) on the same set of axes.
- Use the sketch to determine if \(h\) and \(h^{-1}\) are increasing or decreasing functions.
- Calculate the average gradient of \(h\) between the two points of intersection.
Determine the inverse of the function
\begin{align*} \text{Let } y & = 2x^{2} \qquad (x \ge 0) \\ \text{Interchange } x \text{ and } y: \quad x & = 2y^{2} \qquad (y \ge 0) \\ \frac{x}{2} & = y^{2} \\ y & = \sqrt{\frac{x}{2}} \qquad (x \ge 0, y \geq 0) \\ & \\ \therefore h^{-1}(x) & = \sqrt{\frac{x}{2}} \qquad (x \geq 0) \end{align*}Determine the point of intersection
\begin{align*} 2x^{2} & = \sqrt{\frac{x}{2}} \\ \left( 2x^{2} \right)^{2} & = \left( \sqrt{\frac{x}{2}} \right)^{2} \\ 4x^{4} & = \frac{x}{2} \\ 8x^{4} & = x \\ 8x^{4} - x & = 0 \\ x(8x^{3} - 1) & = 0 \\ \therefore x = 0 &\text{ or } \enspace 8x^{3} - 1 = 0 \\ \text{If } x=0, \quad y & = 0 \\ \text{If } 8x^{3} - 1 & = 0 \\ 8x^{3} & = 1 \\ x^{3} & = \frac{1}{8} \\ \therefore x & = \frac{1}{2} \\ \text{If } x= \frac{1}{2}, \quad y & = \frac{1}{2} \end{align*}Therefore, this gives the points A\((0;0)\) and \(B\left( \frac{1}{2} ; \frac{1}{2}\right)\).
Sketch both graphs on the same system of axes
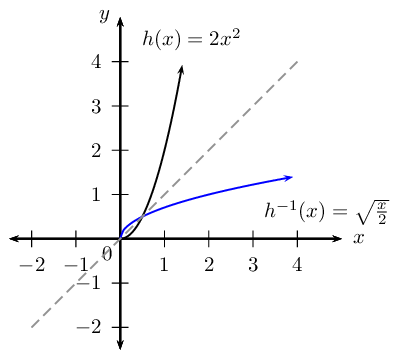
Examine the graphs
From the graphs, we see that both \(h\) and \(h^{-1}\) pass the vertical line test and therefore are functions.
\begin{align*} h: \quad & \text{as } x \text{ increases, } y \text{ also increases, } \text{ therefore } h \text{ is an increasing function. } \\ h^{-1}: \quad & \text{as } x \text{ increases, } y \text{ also increases, } \text{ therefore } h^{-1} \text{ is an increasing function. } \end{align*}Calculate the average gradient
Calculate the average gradient of \(h\) between the points A\((0;0)\) and \(B\left( \frac{1}{2} ; \frac{1}{2}\right)\).
\begin{align*} \text{Average gradient: } &= \frac{y_{B} - y_{A}}{x_{B} - x_{A}} \\ &= \frac{ \frac{1}{2} - 0 }{\frac{1}{2} - 0 } \\ &= 1 \end{align*}Note: this is also the average gradient of \(h^{-1}\) between the points \(A\) and \(B\).
Inverses - average gradient, increasing and decreasing functions
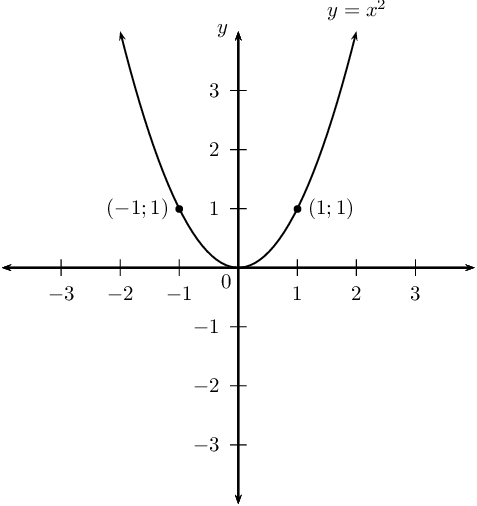
Sketch the graph of \(y={x}^{2}\) and label a point other than the origin on the graph.
Find the equation of the inverse of \(y = x^{2}\).
Sketch the graph of the inverse on the same system of axes.
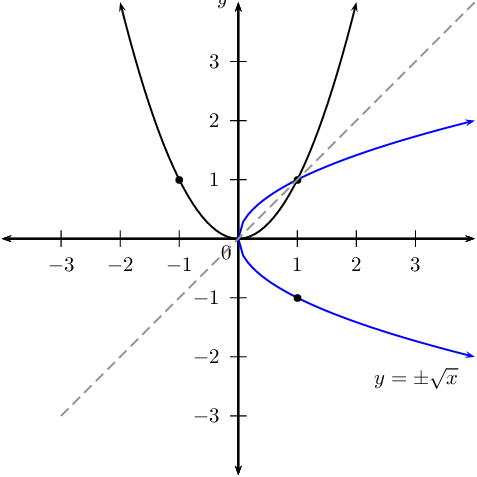
Is the inverse a function? Explain your answer.
No. For certain values of \(x\), the inverse cuts a vertical line in two places. Therefore, it is not function.
\(P(2;4)\) is a point on \(y = x^{2}\). Determine the coordinates of \(Q\), the point on the graph of the inverse which is symmetrical to \(P\) about the line \(y = x\).
Determine the average gradient between:
- the origin and \(P\);
- the origin and \(Q\).
Interpret the answers.
- \begin{align*} \text{Average gradient: } &= \frac{y_{P} - y_{O}}{x_{P} - x_{O}} \\ &= \frac{ 4 - 0 }{2- 0 } \\ &= 2 \end{align*}
- \begin{align*} \text{Average gradient: } &= \frac{y_{Q} - y_{O}}{x_{Q} - x_{O}} \\ &= \frac{ 2 - 0 }{4- 0 } \\ &= \frac{1}{2} \end{align*}
\(\text{Average gradient}_{ OP} = 2\) and \(\text{average gradient}_{ OQ} = \frac{1}{2}\).
Both gradients are positive, and they are also reciprocals of each other.
Given the function \(f^{-1}(x) = kx^{2}\), \(x \ge 0\), which passes through the point \(P \left( \frac{1}{2}; -1 \right)\).
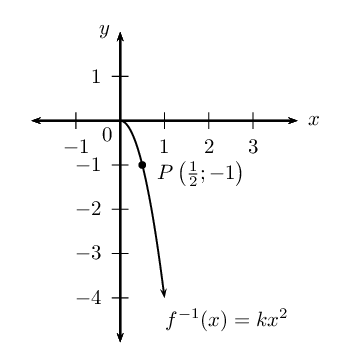
State the domain and range of \(f^{-1}\).
Find the equation of \(f\).
State the domain and range of \(f\).
Sketch the graphs of \(f\) and \(f^{-1}\) on the same system of axes.

Is \(f\) an increasing or decreasing function?
Decreasing function: as the value of \(x\) increases, the function value decreases.
Given: \(g(x) = \frac{5}{2}x^{2}, \enspace x \ge 0\).
Find \(g^{-1}(x)\).
Calculate the point(s) where \(g\) and \(g^{-1}\) intersect.
Therefore, the points of intersection are \((0;0)\) and \(\left( \frac{2}{5};\frac{2}{5} \right)\).
Sketch \(g\) and \(g^{-1}\) on the same set of axes.
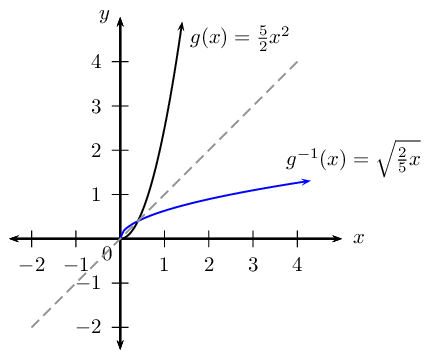
Use the sketch to determine if \(g\) and \(g^{-1}\) are increasing or decreasing functions.
Calculate the average gradient of \(g^{-1}\) between the two points of intersection.
|
Previous
2.4 Linear functions
|
Table of Contents |
Next
2.6 Exponential functions
|
