2.3 Inverse functions
|
Previous
2.2 Functions and relations
|
Next
2.4 Linear functions
|
2.3 Inverse functions (EMCF8)
An inverse function is a function which does the “reverse” of a given function. More formally, if \(f\) is a function with domain \(X\), then \({f}^{-1}\) is its inverse function if and only if \({f}^{-1}\left(f\left(x\right)\right)=x\) for every \(x \in X\).
\begin{align*} & \\ y = f(x) &: \text{indicates a function} \\ & \\ {y}_{1} = f\left({x}_{1}\right) &: \text{indicates we must substitute a specific } x_{1} \text{ value} \\ & \quad \text{into the function to get the corresponding } y_{1}\text{ value} \\ & \\ {f}^{-1}\left(y\right) = x &: \text{indicates the inverse function} \\ & \\ {f}^{-1}\left(y_{1}\right) = {x}_{1} &: \text{indicates we must substitute a specific } y_{1} \text{ value} \\ & \quad \text{into the inverse to return the specific } x_{1}\text{ value} \end{align*}A function must be a one-to-one relation if its inverse is to be a function. If a function \(f\) has an inverse function \(f^{-1}\), then \(f\) is said to be invertible.
Given the function \(f(x)\), we determine the inverse \(f^{-1}(x)\) by:
- interchanging \(x\) and \(y\) in the equation;
- making \(y\) the subject of the equation;
- expressing the new equation in function notation.
Note: if the inverse is not a function then it cannot be written in function notation. For example, the inverse of \(f(x) = 3x^2\) cannot be written as \(f^{-1}(x) = \pm \sqrt{\frac{1}{3}x}\) as it is not a function. We write the inverse as \(y = \pm \sqrt{\frac{1}{3}x}\) and conclude that \(f\) is not invertible.
If we represent the function \(f\) and the inverse function \({f}^{-1}\) graphically, the two graphs are reflected about the line \(y=x\). Any point on the line \(y = x\) has \(x\)- and \(y\)-coordinates with the same numerical value, for example \((-3;-3)\) and \(\left( \frac{4}{5}; \frac{4}{5} \right)\). Therefore interchanging the \(x\)- and \(y\)-values makes no difference.
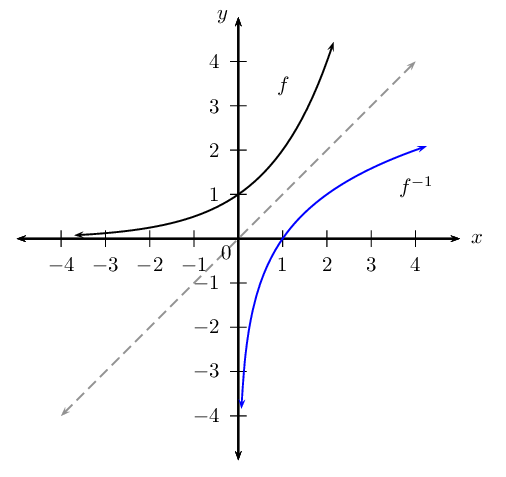
This diagram shows an exponential function (black graph) and its inverse (blue graph) reflected about the line \(y = x\) (grey line).
Important: for \({f}^{-1}\), the superscript \(-\text{1}\) is not an exponent. It is the notation for indicating the inverse of a function. Do not confuse this with exponents, such as \(\left( \frac{1}{2} \right)^{-1}\) or \(3 + x^{-1}\).
Be careful not to confuse the inverse of a function and the reciprocal of a function:
| Inverse | Reciprocal |
| \(f^{-1}(x)\) | \([f(x)]^{-1} = \frac{1}{f(x)}\) |
| \(f(x)\) and \(f^{-1}(x)\) symmetrical about \(y=x\) | \(f(x) \times \frac{1}{f(x)} = 1\) |
| Example: \(\qquad \qquad \qquad \qquad \qquad \qquad\) | Example: \(\qquad \qquad \qquad \qquad \qquad\) |
| \(g(x) = 5x \therefore g^{-1}(x)= \frac{x}{5}\) | \(g(x) = 5x \therefore \frac{1}{g(x)} = \frac{1}{5x}\) |
|
Previous
2.2 Functions and relations
|
Table of Contents |
Next
2.4 Linear functions
|
