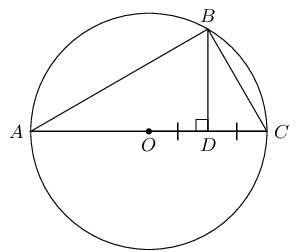
\(B\) is a point on circle with centre \(O\). \(BD \perp AC\) and \(D\) is the midpoint of radius \(OC\).
If the diameter of the circle is \(\text{24}\text{ cm}\), find \(BD\).
Leave answer in simplified surd form.
|
Previous
8.5 Similarity
|
Next
8.7 Summary
|
Many different methods of proving the theorem of Pythagoras have been formulated over the years. Similarity of triangles is one method that provides a neat proof of this important theorem.
The square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides.
(Reason: Pythagoras or \(\text{right-angled } \triangle \text{s}\))
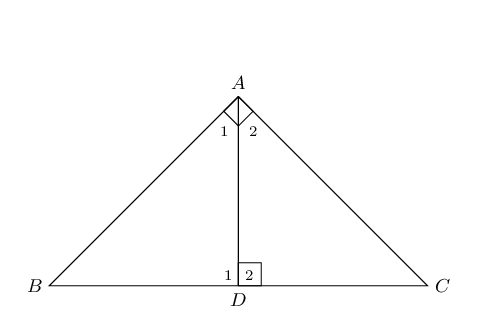
\(\triangle ABC\) with \(\hat{A}=\text{90}°\)
\(B{C}^{2}=A{B}^{2}+A{C}^{2}\)
Construction: draw \(AD \perp BC\).
\[\begin{array}{rll} \hat{C} + \hat{A}_{2} & = \text{90}° & \text{(}\angle \text{s}\text{ of }\triangle CAD \text{)} \\ \hat{A}_{1} + \hat{A}_{2} & = \text{90}° & \text{(given)} \\ \therefore \hat{A}_{1} & = \hat{C} & \\ & & \\ \hat{A}_{1} + \hat{B} & = \text{90}° & \text{(}\angle \text{s}\text{ of }\triangle ABD \text{)} \\ \therefore \hat{B} & = \hat{A}_{2} & \\ & & \\ \hat{D}_{1} & = \hat{D}_{2}= \hat{A} = \text{90}° & \text{(construction)} \\ & & \\ \therefore \triangle ABD \enspace & ||| \enspace \triangle CBA \enspace ||| \enspace \triangle CAD &\text{(AAA)} \\ & & \\ \therefore \frac{AB}{BC}&=\frac{BD}{AB} & (\triangle ABD \enspace ||| \enspace \triangle CBA ) \\ & & \\ AB^{2} &= BD \times BC & \\ & & \\ \text{Similarly } \frac{AC}{CB}&=\frac{DC}{AC} & (\triangle ABD \enspace ||| \enspace \triangle CBA ) \\ & & \\ AC^{2} &= CB \times DC &\\ & & \\ \therefore AC^{2} + AB^{2} &= (BD \times BC) + (CB \times DC ) &\\ &= BC(BD + DC ) & \\ &= BC(BC ) & \\ &= BC^{2}& \\ & & \\ \therefore BC^{2} &= AC^{2} + AB^{2} & \\ \end{array}\]Converse: theorem of Pythagoras
If the square of one side of a triangle is equal to the sum of the squares of the other two sides of the triangle, then the angle included by these two sides is a right angle.
In \(\triangle PQR\), \(P\hat{Q}R = \text{90}°\) and \(QT \perp PR\). If \(PQ = \text{7}\text{ cm}\) and \(QT = 3\sqrt{5} \enspace \text{cm}\), determine \(PR\) and \(QR\) (correct to the nearest integer).
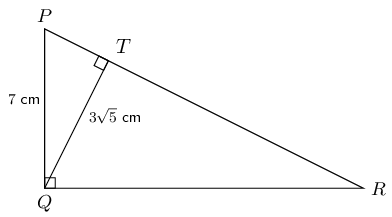
\(PR = \text{25}\text{ cm}\) and \(QR = \text{24}\text{ cm}\)
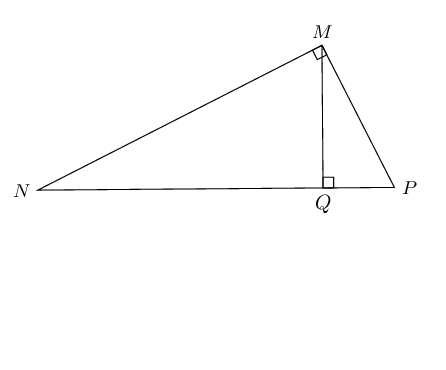
For any right-angled \(\triangle MNP\), if \(MQ\) is drawn perpendicular to \(NP\), then:
\(B\) is a point on circle with centre \(O\). \(BD \perp AC\) and \(D\) is the midpoint of radius \(OC\).
If the diameter of the circle is \(\text{24}\text{ cm}\), find \(BD\).
Leave answer in simplified surd form.

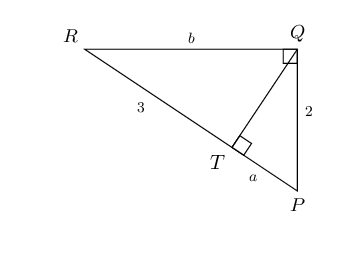
In \(\triangle PQR\), \(RQ \perp QP\) and \(QT \perp RP\). \(PQ = 2\) units, \(QR = b\) units, \(RT = 3\) units and \(TP = a\) units. Determine \(a\) and \(b\), giving reasons.
Chord \(AQ\) of circle with centre \(O\) cuts \(BC\) at right angles at point \(P\).
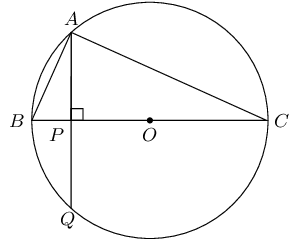
Why is \(\triangle ABP \enspace ||| \enspace \triangle CBA\)?
In \(\triangle ABP\) and \(\triangle CBA\):
\[\begin{array}{rll} B\hat{P}A&= B\hat{A}C =\text{90}° & (\text{given}) \\ \hat{B}&= \hat{B} & (\text{common } \angle) \\ \therefore \triangle ABP& \enspace ||| \enspace \triangle CBA & (\text{AAA}) \end{array}\]If \(AB = \sqrt{6}\) units and \(PO = 2\) units, calculate the radius of the circle.
In \(\triangle ABP\):
\[\begin{array}{rll} AP^{2} &= BA^{2} - BP^{2} & (\text{Pythagoras}) \\ BP &= BO - PO & \\ &= r - 2 & (BO = r, \text{ given } PO = 2) \\ AP^{2} &= \left( \sqrt{6} \right)^{2} - (r-2)^{2} & \\ &= 6 - (r-2)^{2} & \\ & & \\ AP^{2} &= BP.PC & (B\hat{A}C = \text{90}°, AP \perp BC) \\ &= (r-2).PC & \\ \text{And } PC &= PO + OC & \\ &= 2 + r & \\ \therefore AP^{2} &= (r-2)(2 + r) & \end{array}\] \[\begin{array}{rll} 6 - (r-2)^{2} &= (r-2)(2 + r) & \\ 6 - r^{2} + 4r - 4 &= r^{2} - 4 & \\ 2r^{2} - 4r -6 &= 0 & \\ r^{2} - 2r - 3 &= 0 & \\ (r-3)(r+1) &= 0 & \\ r = 3 \text{ or } r &= -1 & \\ \therefore r &= \text{3}\text{ units} & \\ \end{array}\]In the diagram below, \(XZ\) and \(WZ\) are tangents to the circle with centre \(O\) and \(X\hat{Y}Z = \text{90}°\).
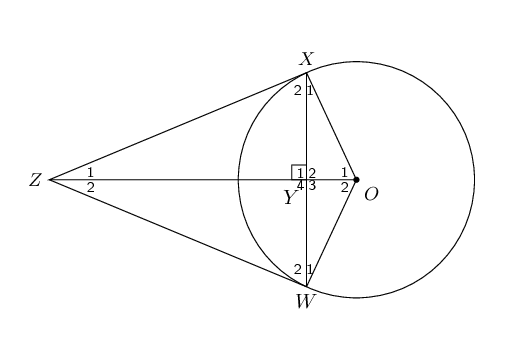
Show that \(XY^{2} = OY \cdot YZ\).
Prove that \(\frac{OY}{YZ} = \frac{OW^{2}}{WZ^{2}}\).
|
Previous
8.5 Similarity
|
Table of Contents |
Next
8.7 Summary
|